三角函数、解三角形创新练习

王思俭

上一篇文章你真的读懂了吗？做一做下面的题目检验一下吧，卡壳的时候先仔细想一想，实在想不出来再去看看文章中是如何讲解的．

1.在△ABC中，AB=2AC，△ABC的面积为3，求BC的最小值．

（变题1-1）在△ABC中，AB=λAC，△ABC的面积为S，设BC=a，求a的最小值．

（变题1-2）在△ABC中，AB=λAC（λ≠1），BC=a，求△ABC面积S的最大值（其中λ，a为定值）．

（变 题1-3）在△ABC中，BC=a，△ABC的面积为S，设AB=λAC，求λ的取值范围（其中a，S为定值）．举个具体例子：在△ABC中，BC=3，△ABC的面积为S=3，设AB=λAC，求λ的取值范围．

答案与解析

1.【法一】设AC=x，AB=2x，BC=a，cosA=

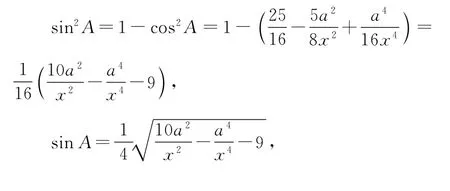
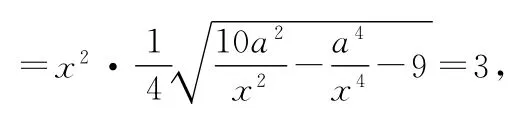
关于x的方程：9x4-10a2x2+a4+144=0有正根，

令t=x2，则关于t的方程：9t2-10a2t+a4+144=0有正根，

于是Δ=100a4-36（a4+144）≥0，得a2≥9，a≥3，

所以a的最小值为3．

【法二】如图1，建立直角坐标系．

设BC=a，B（0，0），C（a，0），A（x，y），

因为AB=2AC，

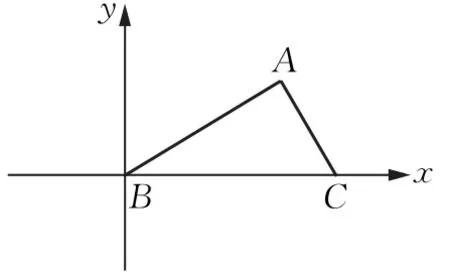
图1

故点A的轨迹是以为圆心，以为半径的圆．

故a的最小值为3．

变题1-1：如图2，建立直角坐标系，B（a，0），C（0，0），设A（x，y），

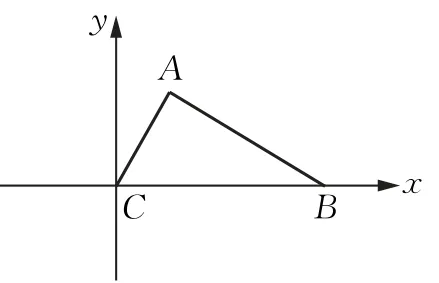
图2

由AB=λAC得到点A的轨迹方程：（x-a）2+y2=λ2（x2+y2），

整理 为：（1-λ2）x2+（1-λ2）y2-2ax+a2=0．

①若λ=1，则点A的轨迹方程是：

即说明点A在线段BC的中垂线上，

此时，BC无最小值，也无最大值；

②若λ≠1且λ＞0，

则点A的轨迹方程是：即说明点A在以为圆心，为半径的圆上，此时，得

故a有最小值

变题1-2：由 变1-1 可 得，故S的最大值为

变题1-3：①λ=1时，成立；

②若λ≠1且λ＞0，

由变1-1知：点A的轨迹方程是：

S=则S=3≤从而

2.思路分析：由已知求得tanα，利用万能公式分别求sin2α，cos2α的值，再展开两角和的正弦求的值．

解法一：由

当tanα=2时，cos2α=

解法二：由已知得设，于是有2t2+5t-3=0．因为再弦化切得，sin将代入得

本题是给式求值类型问题，主要考查三角函数的恒等变换与化简求值，考查两角和的三角函数及万能公式的应用，解法二是拆角变换，设而不求，整体思想，此法简洁明了．