苏州市汽车保有量数据分析与预测
江苏省苏州中学高三(4)班 吾欣仪
截至2018年底,苏州的汽车保有量接近400万辆,位列全国大中城市第五,经报请上级公安机关批准,苏州市公安局交警支队于2019年1月5日按照启用规则,正式启用“苏U”发牌机关代号.可见现有汽车保有量即将超过“苏E”牌照的所有可能组合.苏州也成为江苏省首个启用双号牌的城市.笔者不禁产生疑惑,随着苏州外来人口及人均汽车保有量的增加,多少年后“苏U”牌照资源也将面临枯竭呢?
一、数据收集
通过查询苏州市历年国民经济和社会发展统计公报(网址:http://www.suzhou.gov.cn),得到2010~2018年的汽车保有量,见表1.

表1 2010~2018年苏州市汽车保有量汇总表
二、数据处理与分析
参考表1,将年份代号设为自变量x,汽车保有量设为因变量y,在Excel中列表画图,分别选择学习过的线性函数、二次函数、指数函数、对数函数以及幂函数进行拟合,以线性函数为例,可以得到图1.
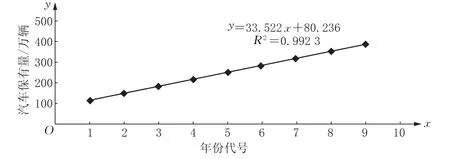
图1 汽车保有量与年份的关系图
由图可知,若选择一次函数模型来考察汽车保有量与年份间的关系,则有y=33.522x+80.236(其中R平方值=0.9923).其中,R平方值又称决定系数,是趋势线拟合程度的指标,它的数值大小可以反映趋势线的估计值与对应的实际数据之间的拟合程度,当趋势线的R平方值等于1或接近1时,其可靠性最高,反之则可靠性较低.
同样地,若选择二次函数来考察汽车保有量与年份间的关系,利用Excel进行数据拟合,则有y=1.228x2+21.241x+102.75(其中R平方值=0.9991);若选择指数函数进行数据拟合,则有y=114e0.1422x(其中R平方值=0.9935);若选择对数函数,则有y=118.97lnx+78.619(其中R平方值=0.8621);若选择幂函数,则有y=109.36x0.5292(其中R平方值=0.9488).
比较五种函数的R平方值,易知二次函数的拟合程度最好.因此,选用二次函数进行拟合,通过计算估算出未来十年苏州的汽车保有量(表2).
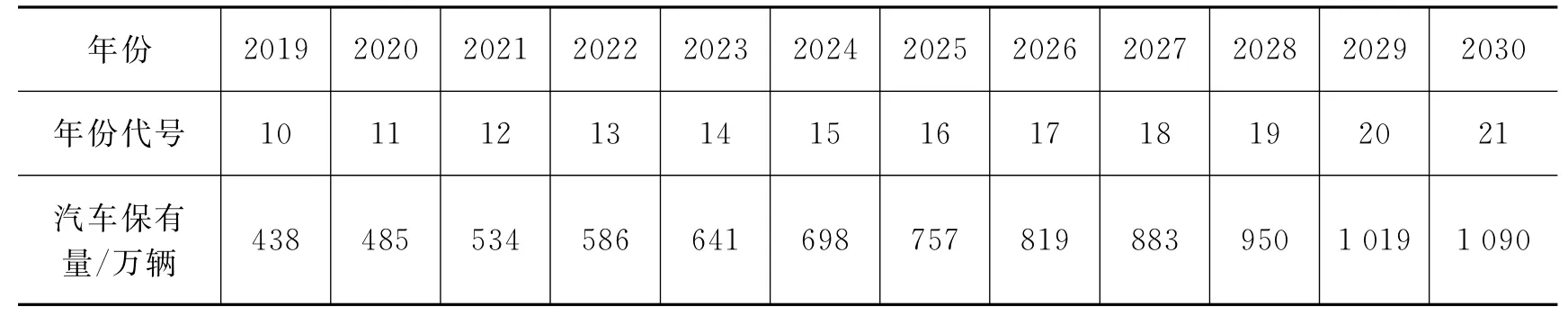
表2 未来十余年苏州汽车保有量预测表
通过数据的拟合可以发现,苏州市汽车保有量将于2029年突破1000万辆.根据现有规定,车牌后五位最多只有两个字母.且为了防止字母I和O与数字1和0混淆,因此车牌中一般没有字母I和O.那么,“苏E”牌照有多少种组合呢?不妨来算一下.
首先,车牌为“苏E”的都可写为“苏E·×××××”,则可分以下三种情况计算:
1.后五位均为数字,共有105种组合;
2.后五位有1个字母和4个数字,有C15×24×104种组合;
3.后五位有2个字母和3个数字,有C25×24×24×103种组合;
以上三种情况合计7.06×106种组合.
那么“苏E”和“苏U”牌照共有1400多万种组合,此外,根据风俗习惯有些组合是不存在的.因此2029年前后将有必要进行新牌照的申请.
三、小结
本文中,笔者利用Excel软件,分析了近几年苏州市汽车保有量的变化趋势,并用二次函数对其进行了拟合.计算发现,苏州市汽车保有量将于2029年突破1000万辆,届时苏U牌照资源也将面临枯竭.
然而,城市的汽车保有量与人口量、居民的消费观念、国家政策等多种因素相关,因此得到的结果并不是精确值,而是会存在一定的误差.
——《2013年中国机动车污染防治年报》(第Ⅰ部分)

