坐标法求立体几何题“四步曲”
南京市第九中学 张荣彬
在空间直角坐标系O-xyz中,分别取与x轴、y轴、z轴方向相同的单位向量i,j,k作为基底,对于空间任意一个向量a,根据空间向量基本定理,存在唯一的有序实数组(x,y,z),使a=xi+yj+zk,则称(x,y,z)为向量a的坐标.空间向量的坐标化,为我们证明空间平行与垂直关系、探求空间角与距离的大小提供了新视野、开辟了新思路.
例1如图1,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE; (2)求二面角A-MA1-N的正弦值.
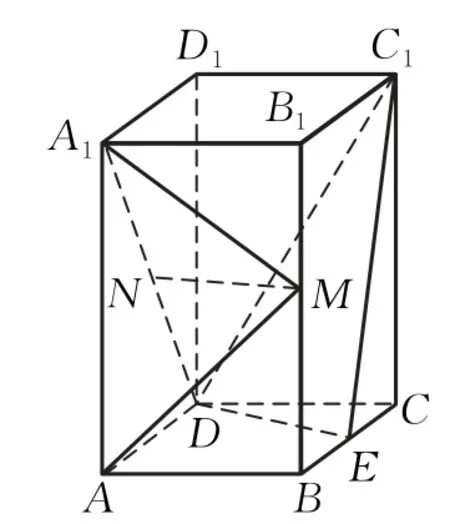
图1
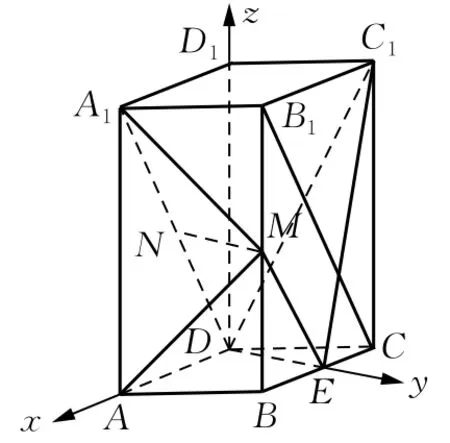
图2
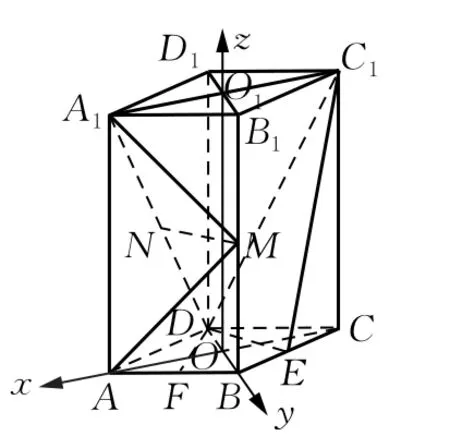
图3
分析直四棱柱ABCD-A1B1C1D1的底面是菱形,∠BAD=60°,可得DE⊥DA.以D为坐标原点,的方向为x轴正方向,建立如图2所示的空间直角坐标系D-xyz,
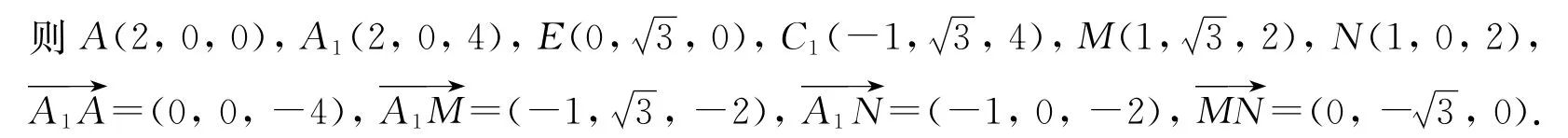
(1)设k=(a,b,c)为平面C1DE的法向量,则取c=1得k=(4,0,1),由于,因MN⊄平面C1DE,所以MN∥平面C1DE.
(2)设m=(x,y,z)为平面A1MA的法向量,n=(p,q,r)为平面A1MN的法向量
从上例可以看出,利用坐标法求解立体几何问题由以下4个环节构成:
(1)建系:建立合适的空间直角坐标系;
(2)求坐标:求出相关点及向量的坐标;
(3)向量运算:利用有关公式进行论证、计算;
(4)结论:将上述运算结果转化为几何结论.
这个解题“四步曲”易被同学们接受,但具体到每个环节,似乎都有些要说的话.
话题1:如何建立空间坐标系?
当确定使用空间向量来解题时,建系就是解决问题的关键所在.建立空间直角坐标系的常用方法有:利用共顶点且相互垂直的三条棱建系、利用线面垂直建系、利用面面垂直建系、利用图形中的对称关系建系.不管何种情形,都是要利用、发现或构造图形中“三垂直”的关系.
(1)题目的背景是长方体、正四棱柱、正方体、直角四面体时,建系无悬念;
(2)正棱锥可以利用底面中心及高所在的直线建系;底面是菱形的直四棱柱,如例1,可利用所给的菱形特征或利用菱形对角线性质(如图3)来建系;对于正三棱柱通常可以参照图4或图5来建系;
(3)除以上特殊图形的常规建系方法外,常会出现一些新的变化.

图4
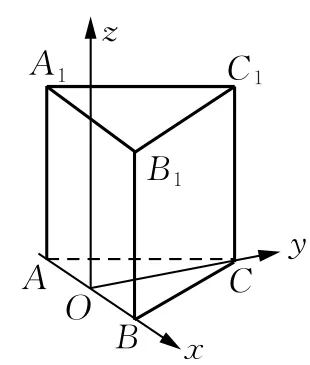
图5
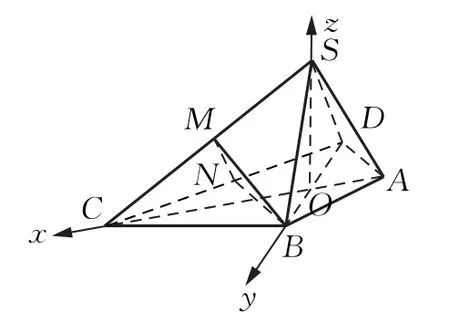
图7
例2如图6,在四棱锥S-ABCD中,△BCD为等边三角形,AD=AB=SD=SB,∠BAD=120°.若二面角S-BD-C为直二面角,求直线AC与平面SCD所成角的正弦值.
分析题中虽然没有现成的三线垂直,但聚焦底面四边形可以发现AC是BD的垂直平分线,设AC与BD交于O,又由SD=SB得SO⊥BD,又SO⊂面SBD,面SBD⊥面ABCD,面SBD∩面ABCD=BD,所以SO⊥平面ABCD.以O为坐标原点,OC,OB,OS所在直线分别为x,y,z轴,建立如图7所示的空间直角坐标系,……
本例坐标系的建立,使用了平面几何知识,也使用了平面垂直的性质定理.虽然说向量坐标化是将几何问题代数化,但在代数化(建系)之前,还需要几何性质的支撑.这是复杂问题建系时的难点所在.
话题2:如何确定点或向量的坐标?
当成功地建立空间直角坐标系后,接下来便是写出相关点的坐标,继而求出有关向量的坐标.一般的方法是先写出xOy平面内点的坐标,然后加上一个“高度”坐标后就是该点正上方的点的坐标了.
(1)画出xOy平面内的真图.
由于空间图形是直观图,因此底面的平面图形可能“失真”,这需要我们借助空间想象写出各点的坐标,必要时也可在草稿纸上画一个真图,这样可以更准确地表示出所求点的坐标.
如例1中的图2、图3及例2中图7,其底面的平面图分别为下面的图8所示,各点坐标容易求得.

图8
(2)利用向量相等求出点的坐标.
例3如图9,在三棱柱ABC-A1BC1中,H是正方形AA1B1B的中心,C1H⊥平面AA1B1B,且试建立合适的坐标系,并写出各点的坐标.
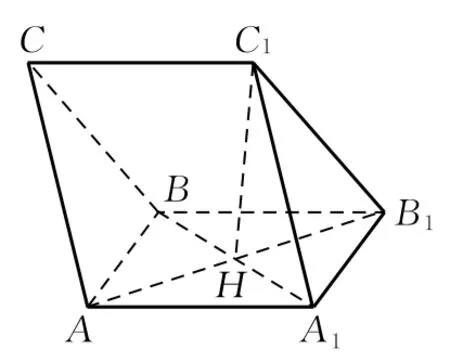
图9
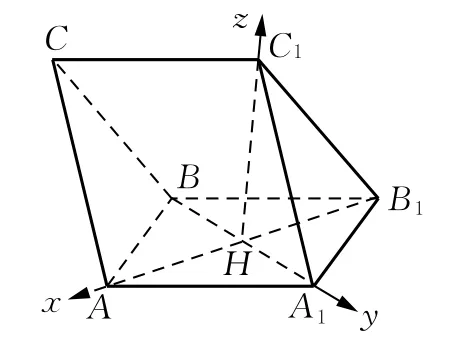
图10
分析如图10,以点H为坐标原点,分别以直线HA,HA1,HC1为x,y,z轴建立空间直角坐标系,依题意得H(0,0,0),A(2,0,0),A1(0,2,0),B(0,-2,0),B1(-2,0,0),C1(0,0,),但点C的坐标如何求出?将它投影到xOy平面内又落在何处?此时可以参考其他信息,比如,设C(x,y,),由向量相等可求出C的坐标.
话题3:判断平行与垂直、求角与距离的大小有哪些向量工具?
直线的方向向量和平面的法向量在研究空间线面位置关系中起着关键作用:
(1)直线与平面、平面与平面的平行与垂直的向量判定方法,主要是借助直线的方向向量与平面的法向量的位置关系来完成;
(2)求异面直线所成的角:异面直线AC,BD的夹角β的余弦值为cosβ=
(3)求直线与平面所成的角:求出斜线的方向向量与平面的法向量所夹的锐角,其余角就是斜线和平面所成的角;
(4)求二面角:二面角的大小就是两平面的法向量所成角(或其补角);
(5)求点到面的距离(如图11)
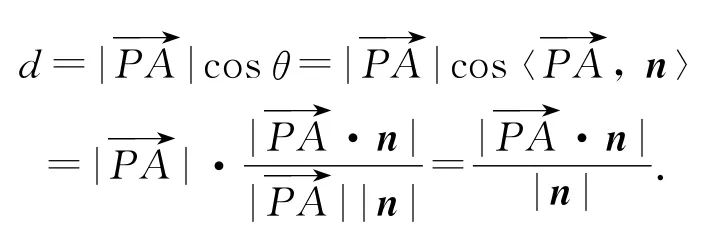
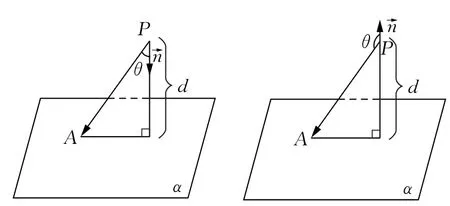
图11
在此公式中,A为平面α内任意一点,解题时只需选择坐标便于计算的点即可,常称为参考向量.这样,我们可以写出求点面距离的一个算法:①求平面的法向量;②选择参考向量;③求参考向量在平面法向量上投影的绝对值.
在例3中,如求A到平面A1B1C1的距离d,可先求平面A1B1C1的法向量n,当确定为参考向量时,则当然用计算也是可行的.直线与平面的距离、平面与平面的距离,都可转化为点到平面的距离.
话题4:怎样用向量运算结果回答立体几何的问题?
这是解题的最后环节,主要是要弄清向量结论与几何问题的关系,如当直线的方向向量与平面的法向量垂直时,要交代线不在面内才可有线面平行的结论;两条异面直线所成的角不一定是两直线的方向向量的夹角;二面角的大小也不一定是两平面法向量的夹角等细节都不能忽视.
——四川美术学院雕塑系建系70周年文献展在重庆开幕

