品形数之美悟数形之妙——《数与形》教学设计与反思

屈 婷 袁凌云

【教学内容】

人教版六年级上册第107页例1。

【教学过程】

一、数与形，各展其长

1.男生女生大PK：第一组题展示给男生，第二组展示给女生，展示后分别计算答题时间定输赢。

第二组：如下图，甲数和乙数相比，（ ）大。

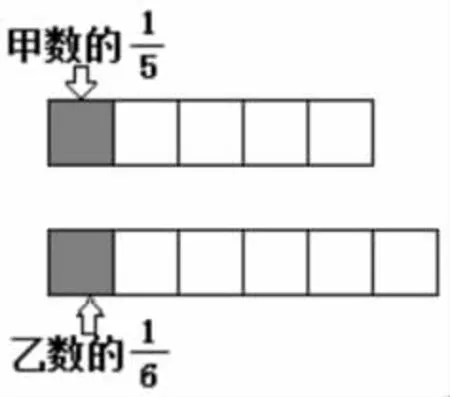
师：同样的题目，为什么女生用时这么少？

小结：虽然问题相同，但给出图形的题目一眼就能看出结果。

2.第二轮PK：

（1）这个角是（ ）角。

（2）一个角的度数是 89°，这个角是（ ）角。

师：这次给女生的题目是数，给男生的是图形，为什么男生又输了？

小结：给出的图形需要测量，给出的角的度数有数据，方便判断角的类型。

师：看来图形和数据都有优点，也有缺点。华罗庚说过：数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休。数形结合到底有哪些好处呢？今天这节课我们就来研究。

【设计意图：在小学阶段，很多数学知识都是在数形结合的基础上逐步抽象概括的，数形结合的思想一直伴随在学生的身边，只是没向学生特别点明。数与形是数学知识的两种不同表征形式，没有高低之分、优劣之说。如何让学生体会数抽象、形直观的特点？笔者为学生提供了两个例子，一是为了唤醒学生对数与形的认识，感受数与形的一路相伴。二是便于让学生初步体会到数与形各有优势：有时数可以助形，利用数的精确能够准确量化形的特征；有时形可以帮数，借助形的直观可以降低数量关系的抽象程度。】

二、图与式，相辅相成

师：如果用一个□表示1，1+3可以怎样画图？1、3分别在图中的哪里？怎样让别人一眼看出1、3在图中的哪个位置？（用不同颜色加以区分）

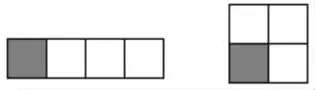
师：一共有多少个小正方形？你是怎么知道的？

板书：1+3 2×2 （4个）

小结：用加法和乘法都可以计算小正方形的个数。

师：1+3+5可以怎样画？画出的图形哪种便于计算？为什么？

小结：画成长方形或不规则图形要一个一个地数，画成正方形更容易用3×3计算结果。

板书：1+3+5 3×3 （9个）

师：同一个正方形，为什么既可以写成两个数相乘的形式，又可以写成几个数连加的形式？这些等式，我们是借助什么得到的？

【设计意图：要实现数形结合，首先要完成数与形的转化。“从1开始的连续奇数相加的算式对应的图不只一种，为什么要研究拼成正方形的形？”这是学生的疑惑之处。因此笔者首先出示“1+3”的算式，让学生构造形，体会形虽然有多种，但数字和图却是一一对应的。接着让学生画出“1+3+5”对应的形，从“多样化的形”到“呈正方形的形”，旨在让学生体会“形”有繁简之分，正方形方格具有明显的图形特征，便于用乘法计算出“1+3+5”的结果。最后，让学生感悟到同样的图形换个角度看，可以产生不同的算法，用两种不同的方式计算同一个几何量，就可以得到一个等式。这样就将数与形进行了沟通与转化，让学生体会到数形之间的密切联系。】

三、想与画，虚实相生

师：按照这样的规律，如果再增加一个加数，你认为是多少？（加7）先想一想，这个算式等于哪两个数相乘，它所对应的正方形边长是多少？再画一画，验证你的猜想是否正确。

师：为什么1+3+5+7还可以写成4×4相乘？除了用图形来解释，这两个算式之间是否也存在内在联系？1+3+5+7这个算式中是否也藏着4？你能找到吗？4在正方形图中是什么意思？

师：结合前面的算式和图看一看，是否也存在这样的规律？这些加数随便是几都可以吗？刚才说增加加数的时候，你们怎么异口同声说要加7？3+5+7可以写成3×3吗？

师：像 1、4、9、16 这些数都可以用一个实心的正方形来表示，这些数是一些和形状有关的数，数学家把它叫做正方形数。1是不是平方数？符合这个规律吗？

师：边长是6的正方形可以转化成哪些算式？如果分割成从1开始的连续奇数相加，加数可能是哪几个？

【设计意图：对于此类问题，不管是数还是形，都有规律可循。规律探寻虽然不是本节课的主旋律，但发现规律的过程能逼着学生把数与形统一起来观察与思考。在这一环节中，笔者让学生先猜想“1+3+5之后接下来该加哪个数”，想象之后再画图，让学生在头脑中先定格图形，再通过画图帮助学生确定想象的图形是否正确，为推算“从1开始的连续奇数连加的结果与平方数之间的关系”打下根基；接着，引导学生发现等式左边加数的个数、等式右边的相同因数与正方形边长的对应关系；最后，把学生的目光聚焦到加数的特点上，明确只有从1开始的连续奇数相加才符合这个规律。在这一过程中，学生利用想象形成的表象，联系画图过程回想，自发将数与图联系起来思考，在整体上把握数与形的对应关系，将数与形结合起来发现规律。】

【教学思考】

一、图式互译，数形转换，架设思维通道

在学生的认知结构中数是数，形是形，难以统一。将数的问题转化成形的问题，从形中寻找计算方法，通过数形的转换，能让学生体会到数与形都是表征问题的方式，由此打通形象思维与抽象思维之间的数学通道。因此，笔者从式引入，给出算式让学生用图形来表征，以形表数，这样就将数的问题转化成形的问题。当学生用直观的图形表征算式之后，让学生指出这些连续奇数分别在图中的什么位置，数形对照，算式与图形一一对应，培养学生寻找数与形对应的能力。如果说“由数想形”是顺向思维的话，那么“见形思数”就是逆向思维。当学生寻找到等式与正方形方格图的规律之后，笔者引导学生思考“边长是6的正方形方格图可以转化成哪些算式？如果分割成从1开始的连续奇数相加，可能是哪几个”，让学生在头脑中对正方形方格进行分拆与计算，与“式”建立联系，经历从图形到算式的回流，培养学生的数形转换能力。

二、内联沟通，数形结合，搭建思维桥梁

图形直观、形象的特点，决定了化数为形能够达到以简驭繁的目的。因此，笔者以直观的正方形方格为载体，引导学生将算式与图形结合起来观察、思考，以形解数，寻找加法算式的简便算法。等式的左右两边，落实到图形中，都是对小正方形个数（或大正方面积）的计算。对一个图形，从不同的角度研究它、计算它，能得到一个等式。“从1开始的连续奇数相加可以用同数相乘来计算，奇数的个数、形态与相乘的因数有怎样的关系，又与正方形的边长有怎样的联系？”这几个问题让学生在反观数与形的关系进而发现规律的过程中，渐渐体会到：规律如果没有直观图形作思考的载体，很难被发现和理解；只通过图形，不借助算式也难以建立正方形数与算式之间的联系。形之于数解释现象的作用逐步发挥出来，数之于形发现规律的价值慢慢被彰显，形数的特点深深印在学生的脑海中。

三、抽丝剥茧，数形互助，打通思维血脉

就数学本质而言，“从1开始的连续奇数相加”可以利用等差数列求和公式“（首项+末项）×项数÷2”来计算。由于这个数列的特殊性，（首项+末项）÷2得到的结果正好与项数（奇数的个数）相等，而奇数的个数正好等于正方形的边长，因此可以写成同数相乘的形式。小学生没有学过数列，难以领略到其中的数学本质，但等差数列的结构特征与构成正方形“L”形的结构特征是有内在联系的。如何通过数形结合的方法让学生逐步体悟正方形数的魅力？当学生探究出规律后，我再次引领学生把算式与图联系起来思考，深究现象背后的道理，让学生进一步感悟到数的结构特征与形的结构特征高度一致，感悟数形之间的密切联系。