让学生在思辨中提升素养——假设策略实践与反思

汪元贵（特级教师）

【教学内容】

苏教版六年级上册第70页例2及相关练习。

【教学过程】

一、创设情境，引出策略

师：今天班里来了这么多的客人老师，相信大家一定都想把自己最光亮的一面展示出来。有信心上好这节课吗？（有）那就开始吧！首先来展示一下同学们解方程的能力。

（课件展示，分组完成）

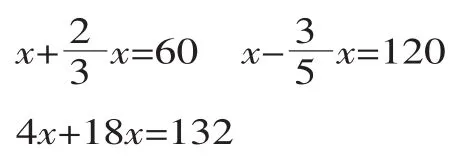
师：正是由于我们的头脑里储备了一定的知识量，才使得我们在解决问题的过程中能够得心应手。

师：在例1学习过程中，我们假设把720毫升的果汁全部倒入小杯或者全部倒入大杯，结果发现杯子的数量改变了，而果汁的总量没有改变。这里运用了假设的策略。其实，这里的“策略”不是最重要的，最重要的是掌握“策略”的人，这个最重要的人是谁呢？让我们在“变”与“不变”中得以见证。

二、探究新知，掌握策略

1.教学例 2。

师：大家都知道，足球运动是我们小学的一大特色，昨天我们的体育老师特地为学校订购了80个球，在快递装盒时，遇到这样一个问题，请看大屏（课件出示）：

在1个大盒和5个同样的小盒里装满球，正好是80个。每个大盒比每个小盒多装8个，大盒里装了多少个球？每个小盒呢？

（全班齐读例2，审题）

（1）“5个同样小盒”说明了什么？

（2）这些球一共有多少个？

（3）一共有几个盒子呢？

（4）大盒与小盒之间有怎样的关系？

（5）根据这个关系，你能列出哪些等量关系式呢？试试看：

①1个大盒里球的个数+5个小盒里球的个数=80。

②1个大盒里球的个数-8=1个小盒里球的个数。

③1个小盒里球的个数+8=1个大盒里球的个数。

师：看来同学们已经把大盒、小盒的关系弄得非常清楚了，这是我们解决问题关键的一步。

师：请观察思考，这里有几个未知量？（2个）出现了2个未知量，用一般的方法来解决就不太方便了，我们能不能学着例1的方法通过假设来把大盒小盒换一换再解决呢？

2.展示并讲解作品。

预设：组1：假设全部是小盒。

（80-8）÷6

=72÷6

=12（个）……小盒

12+8=20（个）……大盒

组2：假设全部是大盒。

（80+5×8）÷6

=（80+40）÷6

=120÷6

=20（个）……大盒

20-8=12（个）……小盒

组3：解：设每个小盒装x个球，则每个大盒装（x+8）个球。

（x+8）+5x=80

6x=80-8

x=12……小盒

12+8=20……大盒

组4：解：设每个大盒装x个球，则每个小盒装（x-8）个球。

x+5（x-8）=80

x+5x-40=80

6x=80+40

x=20……大盒

20-8=12……小盒

师：我们的计算结果对不对呢？还要做进一步的检验（符合题里的所有信息）。

师：想一想：我们在装果汁和装球的过程中，你有什么发现吗？

三、回顾对比，反思策略

（课件出示例1和例2情境图）

预设：

生1：可以通过假设使数量关系变得简单。

生2：例1是杯子的个数改变，果汁的总量不变；例2是盒子的个数不变，而球的总数改变。

师：你的发现真有价值。

四、巩固练习，强化策略

1.商店里的数学。

（“练一练”第一题）指名到黑板上完成。

（1）

（2）“练习十一”第6题。

每个大瓶比每个小瓶多装油2千克，每个大瓶装油多少千克？小瓶呢？

师：数学总是和我们息息相关，它无处不在。我们一起去领略一下森林公园里的数学吧。相信大家一定能出色完成。

2.自然界中的数学。

（1）

（2）

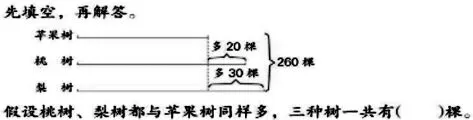
（3）

3.我们身边的数学。

六（5）班杨阳同学参加了一场数学竞赛，一共10道题，每题10分，答错一题倒扣2分，杨阳同学最后得了64分。你知道他答对几道题吗？

师：同学们真的很厉害，有了大胆的设想才会有伟大的发明和发现，你是不是发现“假设法”能把复杂的问题转化为较为简单的问题呢。

五、总结全课，提升策略

【教学反思】

《数学课程标准》指出：“经历观察、实验、猜想、验证等数学活动，发展合情推理能力和初步的演绎推理能力。”强调学生是学习的主人，在学习过程中尽可能多地为学生提供探索和交流的空间，鼓励学生自主探索与合作交流。通过创设的现实情境，让学生投入到解决问题的实践活动中，自己去研究、探索、经历数学学习的全过程，从而体会到假设的数学思想的应用与解决数学问题的关系。通过学习使学生认识到数形结合的重要性，提高学生分析问题和解决问题的能力。在学习中应注意鼓励每个学生参与学习过程，注重学生之间的交流，使学生共同学习、共同进步、共同提高，把所学的数学知识应用到生活中去，用数学的眼光看待身边的事物，体会数学的价值。

本节课最大的特点就是生本课堂理念的充分体现：

1.策略要让学生悟。

数学方法是数学的灵魂，数学的学习对学生来说，绝不仅仅是数学知识的掌握，更为重要的是思想方法的获得。思想方法的获得不能靠外部的输入，而要靠内部萌生。策略的学习关键还在于学生的“悟”，这样获得的方法才根深蒂固。在本课教学中，当数量关系完全理清后，我把学生推向前台，让学生自己通过理解、领会和感悟，体会在假设策略中，什么变了，什么没变，在变与不变中“悟”出用不同的策略解决问题。

2.策略要让学生选。

把自主权还给学生是《数学课程标准》大力倡导的理念之一，学生在充分的交流探讨中，作为课堂的主导者如何让学生欣然接受某种策略好呢？教学时我从学生的实际出发，尊重学生、相信学生，充分发挥学生的主体作用，通过小组探究获得不同的解题策略，在优化策略时，我再次把学生推向前台，让学生讲解自己在感悟中所获得的策略体验，学生在倾听的同时明白，原来解这道题还有这么多的策略。在众多的解题策略出现之后，我又让学生各自发表观点，分析各种策略的优劣，通过甄别达成共识，最后优选出一种最基本的方法。

3.策略在用中提升。

学习知识就是为了更好地应用知识，基于此，精心设计练习也是一节成功的数学课必不可少的重要组成部分。教学中，我把课后习题进行了整合，归为三类：即商店里的数学、自然界里的数学、我们身边的数学。这三类习题无时无刻不在向学生传递一个信息——数学来源于生活又用之于生活。学生在解题过程中，思维能力得以提高，真正达到“学以致用”的高效课堂。

总之，以人为本的数学课堂是灵动的课堂，让学生在不同的体验活动中，感受数学的魅力，享受数学之美。