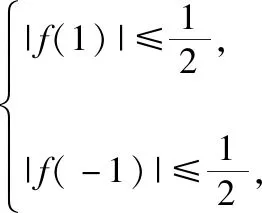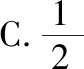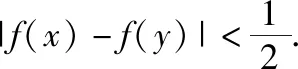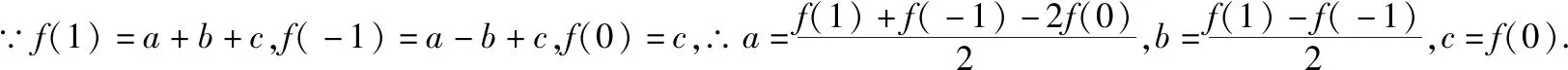处理绝对值题应体现的几种数学意识

黑龙江

王荣峰

(作者单位：黑龙江省鸡西市第一中学)

绝对值是高中数学的核心知识，同时也是高考的高频考点.就命题形式而言，选择题有之，填空题有之，解答题亦有之；就试题的难度而言，简单有之，中档有之，压轴也有之.下面对解绝对值问题应体现的数学意识加以盘点，以期能对读者有所启发和帮助.

1.化归意识

例1.不等式|2x+1|<|x-5|的解集为

( )

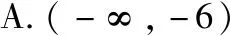
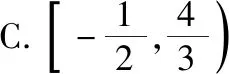
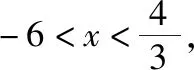
【点评】该题也可通过零点分区间的方法讨论求解，但不如等价平方后，化归为二次不等式来处理更显简洁清晰.

2.取等意识

例2.不等式|2x+lnx|<2x+|lnx|的解集为

( )

A.(0,1] B.(0,1)

C.(1,+∞) D.(-∞,1)

【解析】∵x>0，∴由不等式|2x+lnx|<2x+|lnx|可得|2x+lnx|<|2x|+|lnx|，欲使该不等式成立，只需2x·lnx<0，∴lnx<0，即0

【点评】注意到x>0以及三角不等式|a+b|≤|a|+|b|中等号取到的条件为ab≥0，另辟蹊径，解题思路令人耳目一新.

3.边界意识

例3.若不等式|2x+2|+|x-3|≥a恒成立，则实数a的取值范围是

( )

A.a≤8 B.a≤4

C.4

【解析】设f(x)=|2x+2|+|x-3|，依题意有a≤f(x)min，函数f(x)为“碗状函数”，其最小值必为f(-1)或f(3)，因为f(-1)=4，f(3)=8，从而有a≤4，故选B.

【点评】这种“碗状函数”在各种考试中出现的频率特别高，其形式可以拓展到多个绝对值相加.

4.构造意识

例4.设a,b∈R，则“a>b”是“a|a|>b|b|”的

( )

A.充分不必要条件 B.充要条件

C.必要不充分条件 D.既不充分也不必要条件

【解析】观察题干，可想到构造函数f(x)=x|x|，易知函数f(x)为奇函数，当x∈[0,+∞)时，函数f(x)=x2单调递增，从而可知f(x)=x|x|在R上单调递增,则a>b⟺f(a)>f(b)，故选B.

【点评】观察外部结构特征，构造函数f(x)=x|x|，并借助奇函数的性质使该题巧妙获解，避免了分类讨论带来的繁杂运算.

5.数形意识

例5.若不等式|2x-4|+2

( )

A.a≤1 B.-2

C.-2≤a≤1 D.a≤-2或a>1

【解析】不等式|2x-4|+2

【点评】该题也可通过讨论x的范围进而去掉绝对值来求解，但由于直线g(x)=ax-2过定点P(0,-2)，借助数形结合求解更显直观.

6.讨论意识

例6.若关于x的不等式|2x+a|>x-1*对x∈[-1,2]恒成立，则实数a的取值范围是

( )

A.(-∞,-5)∪[2,+∞) B.(-∞,-5)∪(0,+∞)

C.(-∞,-5)∪(-2,+∞)D.非上述答案

【解析】当x∈[-1,1)时，x-1<0，不等式*对a∈R恒成立；故只需要研究不等式*在x∈[1,2]恒成立即可,此时不等式*等价于2x+a>x-1或2x+a<1-x，由2x+a>x-1得a>-x-1;由2x+a<1-x得a<1-3x.当x∈[1,2]时，(-1-x)max=-2,(1-3x)min=-5，故所求出的实数a的取值范围是a>-2或a<-5，故选C.

【点评】处理绝对值题的基本思路是去掉绝对值，而分类讨论又是去掉绝对值最有效的方法之一，分类讨论的原则是要做到不重不漏.

7.反面意识

例7.若不等式x2<|x-1|+a的解集是区间(-3,3)的子集，则实数a的取值范围是

( )

A.(-∞,7) B.(-∞,7]

C.(-∞,5) D.(-∞,5]

【解析】当x≥1时，原不等式可化为x2-x+1-a<0，其解集中应不含任何大于或等于3的数，故当x≥3时总有x2-x+1-a≥0，由此可得到a≤7；当x<1时，原不等式可化为x2+x-1-a<0，其解集中应不含任何小于或等于-3的数，故当x≤-3时总有x2+x-1-a≥0，由此可得到a≤5，综上可知a≤5，故选D.

【点评】当我们正面探究困难时，也可以考虑从反面切入，往往可以达到事半功倍的效果，本题还可通过数形结合来解决.

8.分离意识

例8.已知函数f(x)=|x-2|+|x-3|，若不等式||2a+b|-|a-b||≤|a|f(x)(a≠0)恒成立，则实数x的取值范围是

( )

A.(-∞,1] B.[4,+∞)

C.[1,4] D.(-∞,1]或[4,+∞)

【点评】类比分离参数的方法，可将|a|除过去，这样就分离出了函数f(x)，再应用绝对值不等式||m|-|n||≤|m+n|就可顺利破解该题.

9.定值意识

例9.已知a，b是任意实数，设|a+b|，|a-b|，|b-2|中的最大值是M，则必有

( )

A.M≥1 B.M≥2

C.0

【解析】根据题意可知4M≥|a+b|+|a-b|+2|b-2|≥|(a+b)-(a-b)|+2|b-2|=2(|b|+|b-2|)≥2|b-(b-2)|=4，从而有M≥1，故选A.

【点评】该题题干虽短，但难度较大，能够用三角不等式|x|+|y|≥|x±y|合理配凑出定值是顺利解出该题的关键点.

10.特值意识

( )

【点评】代入1,-1体现了边界意识，代入特殊值0，一方面由于它是区间[-1,1]的中点，更重要的是代入0可规避掉字母“a”.

11.配凑意识

例11.已知定义在[0,1]上的函数f(x)满足：(1)f(0)=f(1)；(2)对所有的x,y∈[0,1]，且x≠y，有|f(x)-f(y)|<|x-y|，若对所有的x,y∈[0,1]，|f(x)-f(y)|

( )

【点评】该题难度较大，但若能想到插入f(0)和f(1)再进行拆分，进而出现|f(x)-f(0)|+|f(1)-f(y)|，便可找到解决问题的突破口.

12.转化意识

例12.已知函数f(x)=ax2+bx+c，当|x|≤1时，|f(x)|≤2，令g(x)=cx2+bx+a，若当|x|≤1时，|g(x)|≤k恒成立，则实数k的最小值为

( )

A.1 B.2

C.4 D.8

【点评】将字母a,b,c分别用f(1),f(-1),f(0)来表示，并借助|f(1)|≤2，|f(-1)|≤2，|f(0)|≤2就可探究出|g(x)|的最大值，这种代换方法不容易想到，需要解题经验的积累.