刍谈“显性零点”不等式恒成立问题的解决策略

福建

陈尔明

(作者单位：福建省福鼎市第一中学)

显性零点，即通过观察可以得到的函数零点.含“显性零点”的不等式恒成立求参数取值范围的问题在函数与导数压轴题中常有出现，这类问题解决的策略有：(1)分离变量法，此法常伴随几个困难点：一是不易分离或要分类才能分离；二是分离完构造的新函数的单调性不易研究；三是新函数的单调性能研究，但最值要利用洛必达法则才能求出；(2)不分离直接构造函数法，此法多数需要对参数进行分类，对学生的思维严谨性要求较高，最大的思维障碍在于分类点的确立.本文依据教学实践将上述两类策略有机融合，提出了“先猜后求”的分析解决策略，既能避免使用洛必达法则求解造成失分，又能找到分类的切入点，希望对大家有所帮助.

一、“洛必达法则”先行，进而分类解题

例1.(2019·全国卷Ⅰ文·20)已知函数f(x)=2sinx-xcosx-x，f′(x)为f(x)的导数.

(Ⅰ)证明：f′(x)在区间(0，π)存在唯一零点；

(Ⅱ)若x∈[0，π]时，f(x)≥ax，求a的取值范围.

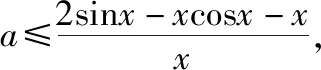
解析：(Ⅰ)略.

(Ⅱ)设g(x)=f(x)-ax，即g(x)=2sinx-xcosx-x-ax，则g(x)≥0在[0，π]恒成立，

又g(0)=0，g′(x)=cosx+xsinx-1-a，设h(x)=g′(x)，则h′(x)=xcosx，

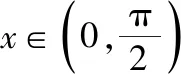
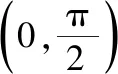
(1)当a≤0时，g′(0)=-a≥0，

若a≤-2，则g′(π)=-2-a≥0，所以g′(x)≥0在x∈[0，π]恒成立，所以g(x)在[0，π]单调递增，g(x)≥g(0)=0恒成立；

所以g(x)在[0，x0]单调递增，在[x0，π]单调递减，又g(0)=0，g(π)=-πa≥0，

所以g(x)≥0恒成立；

(2)当a>0时，g(π)=-πa<0，不合题意；

综上所述，a的取值范围为(-∞，0].

例2.已知函数f(x)=ln(x+1)+ax2，g(x)=ax2-ex-a+e(a∈R).

(Ⅰ)讨论函数f(x)的单调性；

(Ⅱ)当x≥1时，f(x-1)≥g(x)，求a的取值范围.

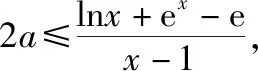
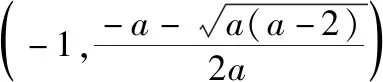
(Ⅱ)依题意得lnx+ex-2ax+2a-e≥0在[1，+∞)恒成立，

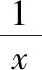
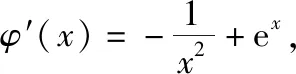
所以φ′(x)≥φ′(1)=e-1>0，所以φ(x)在[1，+∞)单调递增，即h′(x)在[1，+∞)单调递增.

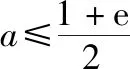
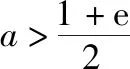
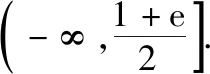
例3.(2017·全国卷Ⅱ文·21)设函数f(x)=(1-x2)ex.

(Ⅰ)讨论f(x)的单调性；

(Ⅱ)当x≥0时，f(x)≤ax+1，求a的取值范围.

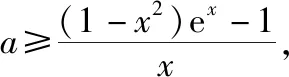
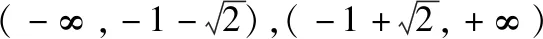
(Ⅱ)设g(x)=(1-x2)ex-ax-1，则g(x)≤0在[0，+∞)恒成立，

又g(0)=0，g′(x)=(1-x2-2x)ex-a，设h(x)=g′(x)，则h′(x)=(-x2-4x-1)ex，

当x∈[0，+∞)时，h′(x)<0，所以g′(x)单调递减，且g′(0)=1-a.

(1)当a≥1时，g′(x)≤g′(0)=1-a≤0，所以g(x)在[0，+∞)单调递减，g(x)≤g(0)=0恒成立；

(2)当a<1时，g′(0)=1-a>0，又g′(x)在[0，+∞)单调递减，所以存在x0>0，当x∈(0，x0)时，g′(x)>0，g(x)单调递增，g(x)>g(0)=0，不合题意；

综上所述，实数a的取值范围为[1，+∞).

二、“边界导数值”先行，进而分类解题

有些含“显性零点”的不等式恒成立问题，不易或不能直接分离变量，此时可以结合函数极限情况控制参数的取值范围，再结合函数单调性的必要条件即边界导数值的符号预测参数范围，而后利用所得参数范围为分类切入点进行分类解题.

例4.已知函数f(x)=(x+2)ex.

(Ⅰ)求函数f(x)的单调区间；

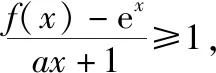
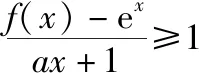
解析：(Ⅰ)函数f(x)的单调递减区间为(-∞，-3)，单调递增区间为(-3，+∞)(过程略).

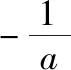
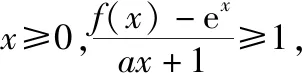
设g(x)=(x+1)ex-ax-1(x≥0)，则g(x)≥0，g(0)=0，

由(Ⅰ)知g′(x)=(x+2)ex-a在[0，+∞)单调递增，且g′(0)=2-a.

当0≤a≤2时，g′(x)≥g′(0)=2-a≥0，所以g(x)在[0，+∞)单调递增，g(x)≥g(0)=0恒成立.

当a>2时，g′(0)=2-a<0，又g′(x)在[0，+∞)单调递增，所以存在x0>0，使得x∈(0，x0)时，g′(x)<0，g(x)单调递减，所以g(x)

综上所述，实数a的取值范围为[0，2].

例5.(2015·山东卷理·21)设函数f(x)=ln(x+1)+a(x2-x)，其中a∈R.

(Ⅰ)讨论函数f(x)极值点的个数，并说明理由；

(Ⅱ)若∀x>0，f(x)≥0成立，求a的取值范围.

分析：第(Ⅱ)问满足f(0)=0属于显性零点问题，若考虑分离变量，需对x2-x进行分类，要分01三类，较为烦琐，且未能探求答案.可以利用边界导数值法猜答案，f(x)≥0恒成立的一个必要条件是f′(0)≥0，可得a≤1.又关注到a<0时，x→+∞，f(x)→-∞，与f(x)≥0矛盾，故a∈[0，1].

(1)当a=0时，由x>0知，f(x)=ln(x+1)>0恒成立；

所以f′(x)在(0，+∞)单调递增，且f′(0)=1-a<0，故存在x0>0，当x∈(0，x0)时，f′(x)<0，f(x)单调递减，所以f(x)

(4)当a<0时，x→+∞，f(x)→-∞，不合题意；

综上所述，实数a的取值范围为[0，1].