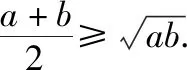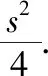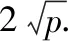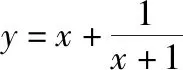探究数学概念与公式的“四层次”构成

河南

周 超

(作者单位：河南省南阳市第二十九中学)

“数学根本上是玩概念的”(李邦河)，学好数学离不开数学概念与公式，但是概念与公式的掌握是不容易的，有经验的老师采取编制口诀和形象化等手段来让学生加深印象，但实际效果却不是很好.

笔者在多年的教学过程中通过观察，并思考发现，大多数数学概念与公式都由“四层次”构成.第一层次是来源背景；第二层次是结构特征；第三层次是变化形式；第四层次是灵活应用.学生如果按照这“四层次”构成来探究数学概念与公式，有利于加深对知识的理解和掌握.

平时在数学学习的过程中，很多学生对概念与公式的认识仅停留在第二层次，甚至对公式结构特征的记忆也是似是而非.原因是很多学生轻视或忽视对数学概念和公式的研究与掌握，总是认为学习数学就是做题目，甚至认为会做题就行，数学概念和公式模糊地知道就行了.学好数学是要适当多做题目，但是概念不清、公式不熟必然影响解题思路和解题速度.

《普通高中数学课程标准(2017年版)》强调了六大核心素养:数学运算、数据分析、直观想象、数学建模、逻辑推理和数学抽象.这六大素养的养成都与数学概念与公式的掌握密不可分.下面通过几个例子来探究一下，如何根据数学概念与公式的“四层次”构成来分析，从而加深对数学概念与公式的理解.

一、单调性，是学好数学的“拦路虎”

单调性是函数最重要的性质之一，是平时考试和高考的热点.而对许多学生来说，函数的单调性的题目做起来会有困难.无论是用单调性定义证明函数在给定区间上的单调性，还是单调性定义的变化形式以及灵活应用，都是我们的“拦路虎”.我们可以尝试用“四层次”构成来探究.

第一层次来源背景:在我们生活的环境中，单调性无处不在，例如太阳东升西落，股市升降变化，汛期水位涨落，甚至人体自身各项指标浮动(比如情绪、智力、体力等)都与单调性有关.而单从数学的观点看单调性，主要是从函数图象的升降中体现的数量变化.

第二层次结构特征:一般地，设函数f(x)的定义域为I:如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2，当x1f(x2))，那么就说函数f(x)在区间D上是增函数(或减函数).

第三层次变化形式:单调性定义的三要素:

①自变量x1,x2的大小关系；

②函数值f(x1),f(x2)的大小关系；

③单调性(增函数或减函数).

根据三要素顺序重组变化产生三种典型题目:

(1)由①②⟹③是用定义证明；

(2)由①③⟹②是比较大小.比如:构造指数函数与对数函数来比较大小；

(3)由②③⟹①是解抽象函数不等式.

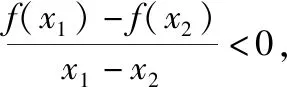
(2)构造单调函数求不等式中参数的范围.

(3)利用函数单调性求最值.

( )

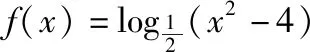
A.(0,+∞) B.(-∞,0)

C.(2,+∞) D.(-∞,-2)

【答案】D.

【例2】函数f(x)在(-∞,+∞)上单调递减，且为奇函数.若f(1)=-1，则满足-1≤f(x-2)≤1的x的取值范围是

( )

A.[-2,2] B.[-1,1]

C.[0,4] D.[1,3]

【答案】D.

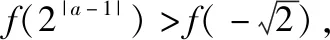
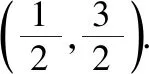
二、等差数列，变与不变的魔法元素

在小学的奥数课里，在七年级数学的第一课找规律里，都有等差数列的影子.

第一层次来源背景:等差数列是一种常见的数列.等差现象广泛存在于生活中，例如鞋码的大小、堆放的钢管和电影院里的座位号等，都是从第二项起，后一项与前一项的差是同一个常数.

第二层次结构特征:等差数列的定义及通项公式，an+1-an=d,an=a1+(n-1)d，首项a1、公差d、项数n、第n项an.

第三层次变化形式:等差数列通项公式的四种变化形式如下:

a1=an-(n-1)d;

an=am-(n-m)d;

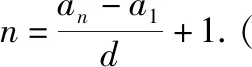
从上各式都是通项公式的变形，虽然形式不同，但都是对通项公式的等价变换.

第四层次灵活应用:

(1)等差数列中项的性质

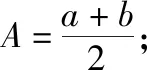
(2)对称项的性质

若m,n,k,p,q∈N*,且m+k=p+q=n+1.

则a1+an=a2+an-1=am+ak=ap+aq；

(3)通项公式是关于n的一次式an=an+b.(a、b是常数)；

(4)等差数列前n项和的性质；

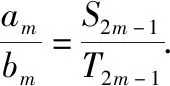
【例4】记等差数列{an}的前n项和为Sn，若a3=0，a6+a7=14，则S7=________.

【答案】14.

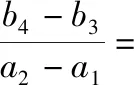
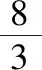
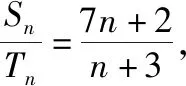
三、两角和的正切函数，合作才能共赢

在两角和差的三角函数里，正切函数没有正弦余弦活跃，但是涉及正切函数的题目，式子变化相对复杂，解起来有一定的难度.

第一层次来源背景:正切函数定义，同角三角函数关系，非特殊角化为特殊角.

第二层次结构特征:两角和的正切由α与β正切的和与积构成.

tan(α+β)-tanα-tanβ=tan(α+β)tanαtanβ(α,β为任意角).

第三层次变化形式:

(3)(诱导公式)

tan(π+α)=tanα;

tan(2π-α)=-tanα.

(4)tan(α+β+γ)

第四层次灵活应用:

(1)由α+β=45°，推得(1+tanα)(1+tanβ)=2.

推广:(1+tan1°)·(1+tan2°)·(1+tan3°)…(1+tan43°)·(1+tan44°)=222.

(2)在△ABC中，

tanA+tanB+tanC=tanAtanBtanC.

( )

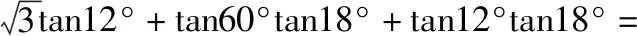
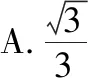
C.1 D.3

【答案】C.

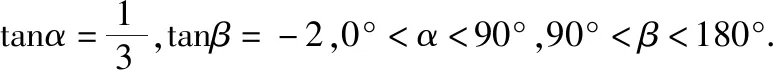
求证:α+β=135°.

【答案】证明略.

( )

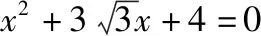
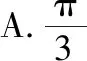
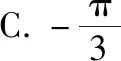
【答案】D.

四、向量的投影，排疑解难的“大侠”

第一层次来源背景：(1)两向量的夹角定义；(2)两向量数量积几何意义的需求.

第二层次结构特征:向量b在向量a上的投影|b|cosθ(θ为向量a，b夹角).

第四层次灵活应用:(1)证明正弦定理;(2)几何概率面积之比.

( )

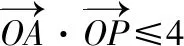
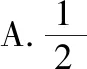
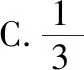
【答案】D.

【例11】已知a=(2,0),b(-1,2),则b在a方向上的投影为________.

【答案】-1.

【例12】在等腰三角形ABC中，AB=AC=2,∠ABC=30°，D为BC的中点.

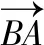
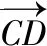
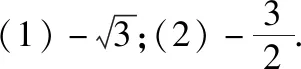
五、正弦定理，边角对应见真情

三角形是最简单的多边形，又是内容最丰富的多边形，三角形的知识直观地告诉人们“简单就是丰富”这个真理.

第一层次来源背景：三角形的边与对应角的正弦之比相等是三角形固有的关系.

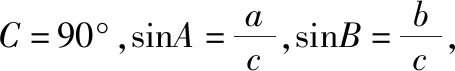
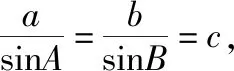
因为C=90°，sinC=1，

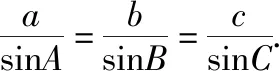
这个优美的关系式对等边三角形也成立，对其他的任意三角形是否成立呢？

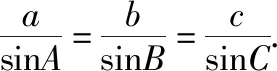
第三层次变化形式:

(1)a∶b∶c=sinA∶sinB∶sinC；

(3)a=2RsinA，b=2RsinB，c=2RsinC(R为三角形外接圆半径).

第四层灵活应用:(1)边化角，角化边；

(2)A

(3)与三角形面积的关系:

S△ABC=2R2sinAsinBsinC.

【例14】在△ABC中，满足acosB=bcosA，则△ABC的形状为

( )

A.直角三角形 B.锐角三角形

C.钝角三角形 D.等腰三角形

【答案】D.

【例15】在△ABC中，已知(b+c)∶(c+a)∶(a+b)=4∶5∶6,则sinA∶sinB∶sinC等于

( )

A.6∶5∶4 B.7∶5∶3

C.3∶5∶7 D.4∶5∶6

【答案】B.

六、基本不等式，变大变小广思路

第一层次来源背景:

若a,b∈R,则(a-b)2≥0.

即a2+b2≥2ab.

第三层次变化形式:

(2)2(a2+b2)≥(a+b)2；

第四层次灵活应用:(1)凑定值求最值;

(2)利用化“1”的思想.

【答案】1.

【答案】4.

【答案】(-∞,4].