细品方知题真味——2019年全国卷Ⅰ理科概率压轴题的探究

广东

林国红

(作者单位：广东省佛山市乐从中学)

2019年高考结束后，多数考生反馈全国卷Ⅰ理科数学的难度较高.其中最令人瞩目的是第21题(解答题的压轴题)，题目考查的是概率的内容，而将对概率的考查作为解答题的压轴题，在近几年高考全国卷中是史无前例的.由于此题字数较多，阅读量大，情景陌生，而且除了考查概率的知识外，还综合考查等比数列的证明与数列的其他相关知识，所以令考生望而生畏.本文将对此题进行解答分析，并进行深入探究，希望能起到抛砖引玉的效果.

一、题目呈现与解答

【题目】为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验.试验方案如下：每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠，随机选一只施以甲药，另一只施以乙药.一轮的治疗结果得出后，再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效.为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得-1分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得-1分；若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X.

(Ⅰ)求X的分布列；

(Ⅱ)若甲药、乙药在试验开始时都赋予4分，pi(i=0,1,…,8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0=0，p8=1，pi=api-1+bpi+cpi+1(i=1,2,…,7)，其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5，β=0.8.

(ⅰ)证明：{pi+1-pi}(i=0,1,2,…,7)为等比数列；

(ⅱ)求p4，并根据p4的值解释这种试验方案的合理性.

【解答】(Ⅰ)X的所有可能取值为-1,0,1.于是P(X=-1)=(1-α)β，P(X=0)=αβ+(1-α)(1-β)，P(X=1)=α(1-β).

所以X的分布列为

X-101P(1-α)βαβ+(1-α)(1-β)α(1-β)

(Ⅱ)(ⅰ)因为α=0.5，β=0.8，由(Ⅰ)得a=P(X=-1)=0.4,b=P(X=0)=0.5，c=P(X=1)=0.1.

因为pi=api-1+bpi+cpi+1，所以pi=0.4pi-1+0.5pi+0.1pi+1，故0.1(pi+1-pi)=0.4(pi-pi-1)，即pi+1-pi=4(pi-pi-1).

又因为p1-p0=p1≠0，所以{pi+1-pi}(i=0,1,2,…,7)为公比为4，首项为p1的等比数列.

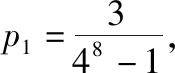
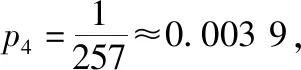
【评注】①问题(Ⅰ)只要正确理解题意，就能将其转化为大家耳熟能详的离散型随机变量分布列，相对简单.问题(Ⅱ)(ⅰ)中证明数列为等比数列，利用题目中已经给出的递推公式和α=0.5，β=0.8这两个条件，用到的是常规解法.问题(Ⅱ)(ⅱ)用大家熟悉的累加法求出等比数列通项公式，不难算出结果.最后根据概率极小说明试验方案的合理性也是较为容易的.

②试题的解答方法是常规的，计算量也适中，这与教育部考试中心的“多考一点想的，少考一点算的”的命题精神相吻合.

③试题的难点是题目阅读量较大，对学生造成了较大的负担.会导致无法正确理解题意或者学生的运算出错等失误，另外试题放在最后压轴题的位置出乎了考生意料，给考生造成了巨大的心理压力.

二、解法优化

在上述解答中，问题(Ⅱ)(ⅱ)的做法是可以优化的，过程如下：

由(ⅰ)可知{pi+1-pi}(i=0,1,2,…,7)为公比为4，首项为p1的等比数列.所以可得pi+1-pi=4ip1.

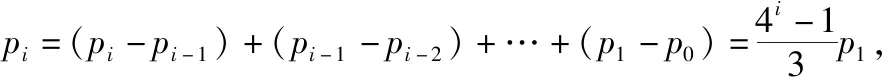
从上面的解答过程，可以看出不用求出p1，同时p4的计算也得到了简化.

三、问题(Ⅱ)的一般化

在解答完本题后，思考：若试题没有给出α与β的数值，问题(Ⅱ)还能不能解答？如果能，p4如何表示？

答案是肯定的，解答的思路与过程跟原题解答类似.

因为a=P(X=-1)=(1-α)β，b=P(X=0)=αβ+(1-α)(1-β)，c=P(X=1)=α(1-β)，且pi=api-1+bpi+cpi+1.

所以pi=(1-α)βpi-1+[αβ+(1-α)(1-β)]pi+α(1-β)pi+1，

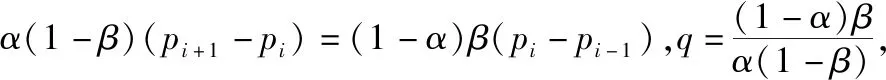
又因为p1-p0=p1≠0，所以{pi+1-pi}是以公比为q，首项为p1的等比数列，于是可得pi+1-pi=qip1.

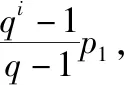
显然，当α=0.5，β=0.8时，q=4，这正是原试题的情形.

四、初始条件与递推公式的由来

试题中所给出的初始条件p0=0，p8=1和递推公式pi=api-1+bpi+cpi+1是否合理？能否根据题意推出初始条件和递推公式呢？

事实上，是不需要给出初始条件和递推公式的，这些可以根据题意推出来！

依题意知，当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈白鼠只数多的药更有效.甲药、乙药在试验开始时都赋予4分，pi(i=0,1,…,8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，依照约定，可知每轮得分之和均为0，于是两人得分之和始终不变，保持是8分.每多治愈一只白鼠则比对方多得2分，则若甲得0分，则乙得8分，故乙治愈的白鼠比甲多4只，实验即可停止，故有p0=0，同理p8=1.

若甲得分为i，考虑下一轮，要么变为i-1，要么不变，要么变为i+1，其相应的概率恰为a,b,c.从而得到pi=api-1+bpi+cpi+1，其中a=P(X=-1),b=P(X=0),c=P(X=1).

所以试题完全可以不给初始条件p0=0，p8=1和递推公式，试题把最难的求递推公式部分直接给出来，实际是为了降低难度.而且问题(Ⅱ)(ⅰ)等比数列的证明其实也是可以不要的，之所以要证明等比数列也是为了降低难度，是命题老师给考生提示解题思路的.这样做更好地控制了整道试题的难度，让考生更容易解答.

当然如果试题不给初始条件和递推公式，直接问最后一问，那样试题的难度就大大提升了，而且在没有提示的情况下作为高考题，也是违背全国卷的命题原则的，因为近年来全国卷一直坚持的原则是数列简化，一般不考查由数列递推公式经过复杂的变形求出数列通项公式的问题.如果要考查此类问题，一般会先证明一个辅助数列是等差或者等比数列，也就是像试题中那样，所以此题中所涉及的数列内容是较常规的考查形式.

五、追本溯源

问“题”那得清如许，为有源头活水来.原试题的题源来自于：

(2018年湖南省高中数学联赛预赛B卷第12题)棋盘上标有第0,1,2,…,100站，棋子开始时位于第0站，棋手抛掷均匀硬币走跳棋游戏.若掷出正面，棋子向前跳出一站；若掷出反面，棋子向前跳出两站，直到跳到第99站(胜利大本营)或第100站(失败大本营)时，游戏结束.设棋子跳到第n站的概率为pn.

(Ⅰ)求p3的值；

(Ⅲ)求p99，p100的值.

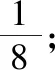
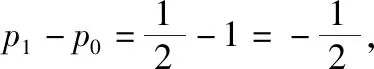
【评注】①高考题的问题(Ⅱ)与联赛题的问题(Ⅱ)(Ⅲ)基本一致，联赛题可以看作高考题的“题源”，高考题将本题进行适当的改编，赋予更丰富的命题背景，这说明命题专家很重视命题的传承和相互借鉴.所以在高考的备考中，除了要进行高考真题的训练外，还可以适当加入一些接近高考难度的高中数学联赛题的训练.

②对试题的探源，可以让我们更深刻地认识问题，教师要善于钻研高考题，用“慧眼”去发现有典型性、可拓展性的高考题，善于进行解后反思，方法的归类，规律的总结与技巧的揣摩，再进一步对题目进行挖掘、拓展、延伸，扩大考题的辐射面，以此提高复习的效率.

六、试题的概率论背景

这道概率题是命题人站在随机过程的马尔可夫链(Markov Chain)角度命制的题目.马尔可夫链，又称离散时间马尔可夫链，因俄国数学家安德烈·马尔可夫得名，是状态空间中经过从一个状态到另一个状态的转换的随机过程.该过程要求具备“无记忆”的性质：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关.这种特定类型的“无记忆性”称作马尔可夫性质.在马尔可夫链的每一步，系统根据概率分布，可以从一个状态变到另一个状态，也可以保持当前状态.状态的改变叫做转移，与不同的状态改变相关的概率叫做转移概率.下图是一种最简单的马尔可夫链：随机游走(Random Walk)的示意图，这是概率论中著名的“直线上的随机游走问题”.本试题相当于是随机游走的一个变种，增加了一种分数维持不变的可能性.本题相当于有两个边界0和8，到达边界后即停止，所以更准确地说是“有双侧吸收壁的直线上的随机游走问题”.

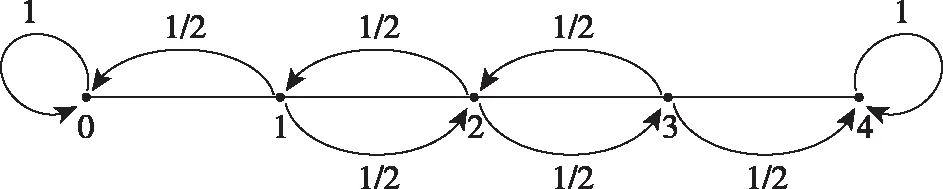
马尔可夫链的本质较为简单，就是一个事件之后的状态只取决于上一步的状态.例如在本试题中，第i+1次试验之后两种药的分数，只会基于第i次试验之后的分数+1/0/-1，所以之前的分数是多少就不需要知道，只知道第i次实验之后的分数就足够进行推测了.

题目中甲药的分数就是这样一个马尔可夫链，而我们关心甲药的分数和最后“试验表明甲药更有效”的概率之间的关系，这就要关系到甲药在不同分数之间转移的概率，就是题目中所给的递推式：pi=api-1+bpi+cpi+1，这个关系式本质上表达了马尔可夫链的传递规律，从pi由概率a传递到pi-1，由概率b留在pi，由概率c传递到pi+1.所以从pi出发，最终获胜的概率也是如此传递的.给出这个关系式实质上大大降低了题目的难度，避免了考生因为不熟悉题目的背景而束手无策的问题.试题设计注重对问题背景的理解，将大学随机过程的知识融在高中数列的角度中让考生分析，本质上只需要高中数学的数列知识，而不需要复杂的计算工具.

马尔可夫链是概率论中重要的一类问题，应用非常广泛，有兴趣的读者可以查阅概率论的专业书籍进一步学习.

七、试题的启示

近几年全国卷Ⅰ的概率统计大题考查的知识点与背景不稳定，每年都有变化，例如2018年全国卷Ⅰ理科第20题结合了函数与导数，今年结合了数列.这种灵活多变的考题给考生的复习备考带来了很多不确定性，也正是由于这种不确定性，对每位考生来说是最公平的.命题人教育理念新，专业知识精，选拔标准高，命制的试题超出一线教师的想象，但总能源于教材，高于教材，契合新课标的精神.

高考全国卷概率统计大题具有以能力立意、综合性强和思维量大等特点，且实际背景新颖，对阅读理解、推理分析和数据运算的要求较高，因此难度较大，但近两年降低了运算的难度.统计背景下的概率题弱化计数问题，侧重于统计思想，数据分析与处理，结合生活实际的决策性问题，突出数学的应用意识,突出学科素养导向，注重考查数学应用，体现综合性和应用性的考查要求.试卷设置的情境真实、贴近生活，体现数学原理和方法在解决问题中的价值和作用.这有利于在中学数学教育中激发学生学习数学的热情，提高学生对数学价值的认识，提升学生的数学素养，对中学的素质教育有很好的导向和促进作用.