探究让课堂更精彩

安徽

陈晓明

(作者单位：安徽省宁国中学)

本文所讨论的试题是笔者所在学校(省级示范高中)高一的一道数学周考试题，是关于直线方程的解答题，此题得分率很低，于是在试卷讲评课上笔者带领学生对该题的解法一探究竟，以求找到不同解法及诸多错解产生的原因，并掌握此类问题的解题策略.结果同学们积极参与讨论，课堂上精彩纷呈，带来好多意外收获！

一、课堂实录

题目直线y=2x是△ABC中∠C的平分线所在的直线l，若点A,B的坐标分别为A(-4,2)，B(3,1)，求点C的坐标，并判断△ABC的形状.

教师：谁来谈谈自己的看法？

学生1：要想求点C的坐标，只需要求出直线CA或CB的方程即可.因为点C又在直线l：y=2x上，所以联立直线l与直线CA或CB的方程，解方程组即可得到点C的坐标.可我无法求出直线CA或CB的方程，因为只知道直线上一个点的坐标.

教师：分析很有道理，做数学题首先就要像学生1一样会分析.谁能帮他解决分析过程中遇到的困惑呢？

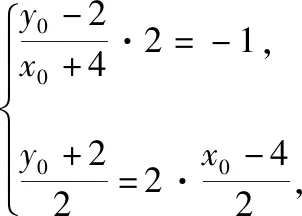
进一步求出直线CB(即直线CA′)的方程为3x+y-10=0.

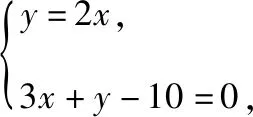
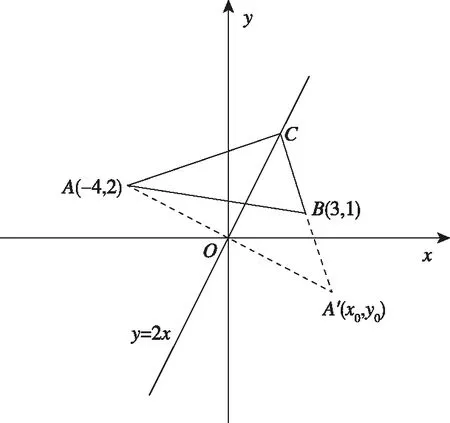
教师：太厉害了！充分利用了角平分线的性质，求得点A(-4,2)关于直线l的对称点A′(4,-2)，从而利用两点坐标求得直线CB的方程，问题迎刃而解.

学生3：我还求出了点B(3,1)关于直线l的对称点B′(-1,3)，因为点B′(-1,3)在直线CA上，从而求出直线CA的方程，再利用直线CA与l的方程求得点C的坐标，这样做麻烦一些，我当时没想到学生2的简单方法.

教师：两位同学的解法都非常好！其他同学还有更好的想法吗？

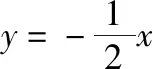
教师：聪明！真是“条条大路通罗马”.

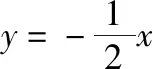
教师：很好，真是殊途同归！我当初还真没想到求对称点也有这么多方法.

学生6：我觉得在前面学生3的方法中，求得点C的坐标后，求出直线CA与CB的斜率，由它们的斜率之积为-1，即可得两直线垂直，从而得到△ABC为直角三角形.

学生7：这只能判断出∠C为直角，无法判断是否等腰.

教师：数学使人周密真是没错.

就在这时，平时一直不太爱说话的学生8也发言了，不过看他样子好像十分困惑.

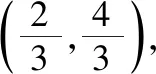
教师：大家思考一下这是什么原因呢？是解法1漏解了，还是解法2产生了增解？

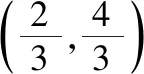
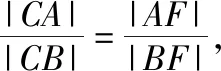
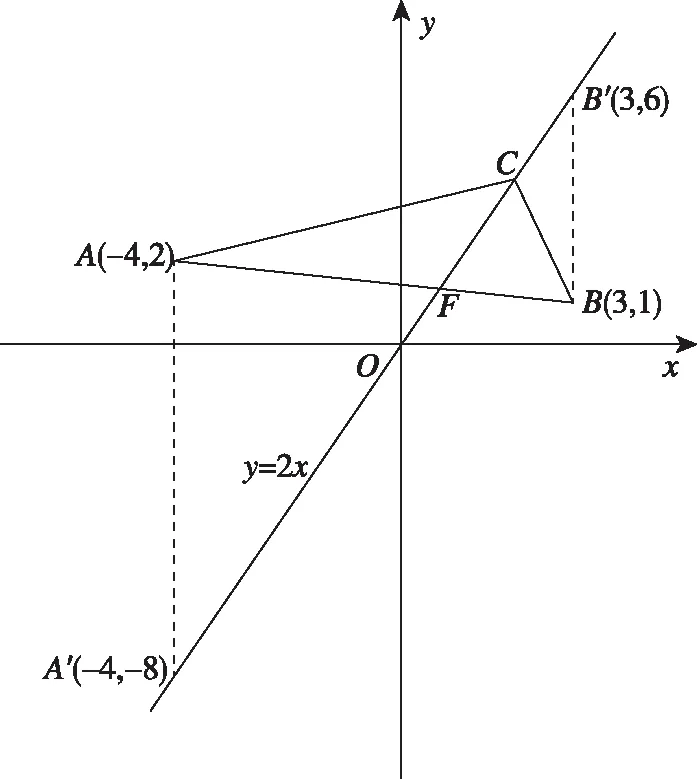
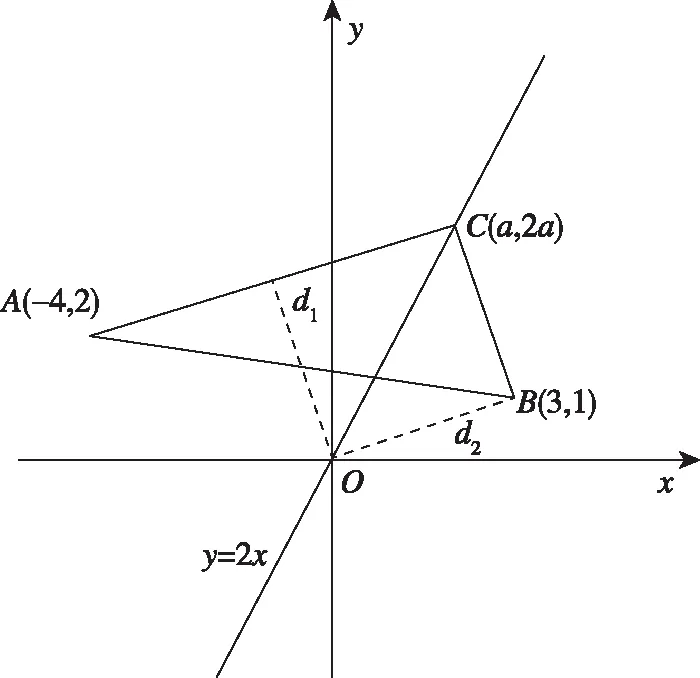
学生10(解法3：利用相似三角形)：如图所示，分别过点A(-4,2)，B(3,1)作x轴垂线，与直线l：y=2x分别交于点A′(-4,-8)，B′(3,6).

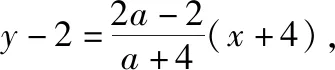
教师：看似复杂的方法，运算却很简单，看来学习数学要不畏艰难，敢于挑战，最后你可能会发现拦路虎原来是纸老虎！

接下来又有同学提出一些问题，大家一同进行了研究.

教师：大家通过对此题的研究得到了什么启示？

学生各抒己见，概括起来主要是下面几点：

①所研究问题与以前的哪些问题相类似，解决此类问题的基本思路是什么？

②解题的关键在哪里？是如何化归的？

③本题是否有别的解法？有无更简便的解法？

④哪一种方法最基本？哪一种方法最典型？哪一种方法最简便？哪一种方法最巧妙?

⑤解题结果是否正确、圆满？有无增解、漏解或错解等情况？

二、教学思考

“灯不挑不明，理不辩不清”，教师要充分利用学生对试题的错误解法，给学生多一些思考，多一些探究，要充分相信学生，不能只按照自己事先想好的思路来教学，否则就会限制学生的思维，强扭学生的思维，题目刚出来就先进行提示或分析，那样做会扼杀学生的自主思维能力，剥夺学生的自由创造空间.在学生还没来得及思考的时候，老师硬是用自己固定的思路框定他们的头脑，使他们服从于已有的模式，这对他们思维能力的形成是个不小的打击.

离开了学生的“自主活动”“智力参与”“个人体验”，就失去了学习真正的意义了.把课堂还给学生，引导学生积极思考，让每位学生在数学思维的世界里自由地翱翔，体现出习题课教学的作用，通过解决问题，促进学生对数学知识的理解，让每位学生主动、积极地参与教学.当然，要做到这点，首先，教师对习题本身要有深入的研究，其次，对学生的课堂参与要给予足够的激励和引导，注意倾听他们的声音，点燃他们的思维之火.

《普通高中数学课程标准(实验)》强调：“数学教学要使学生通过不同形式的自主学习、探究活动，体验数学发现和创造的历程.”作为一线教师，我们应力求让探究成为数学课堂教学的常态，应善于把握课堂教学中的每一个探究机会和细节，使数学探究逐步成为学生学习的自觉行为，乃至形成习惯，促进学生思维的全面发展.