从课本习题到高考题的探究

辽宁

孟庆杰

(作者单位：辽宁省抚顺市四方高级中学)

探究式教学模式的主要目标是学习发现问题的方法，培养创造性思维.它通过教师精心设置问题链，引导学生对问题进行论证，形成确切的概念；引导学生分析解题过程，形成新的认知结构.在实际教学中，发现课本中有些习题与高考题有关，下面结合课本习题，给读者一个探究发现的平台.

一、课本习题的探究

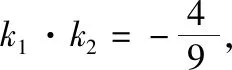
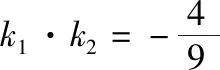
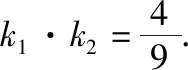
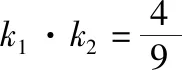
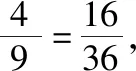
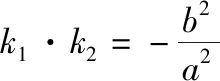
二、高考题的探究

请同学们解决下列高考题：

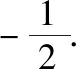
求C的方程，并说明C是什么曲线.

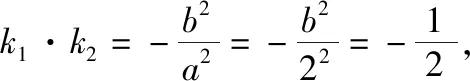
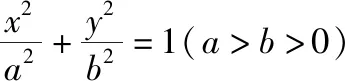
(Ⅰ)求椭圆和双曲线的标准方程；

(Ⅱ)设直线PF1，PF2的斜率分别为k1，k2，证明：k1·k2=1；

(Ⅲ)是否存在常数λ，使得|AB|+|CD|=λ|AB|·|CD|恒成立？若存在，求λ的值；若不存在，请说明理由.

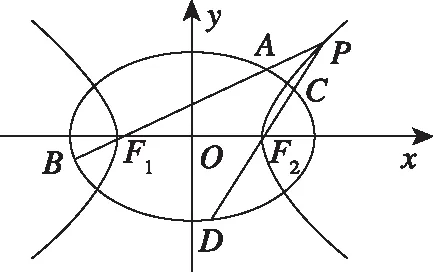
三、探究高考题的推广

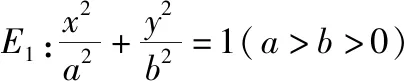
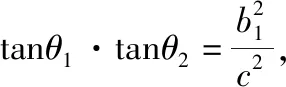
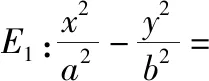
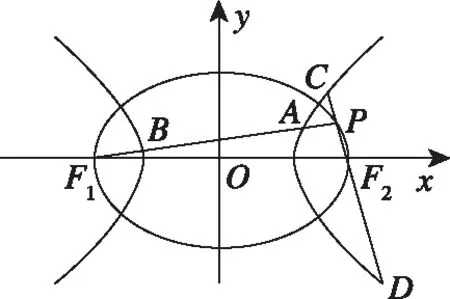
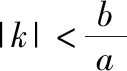
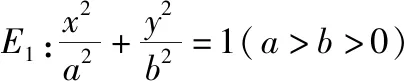
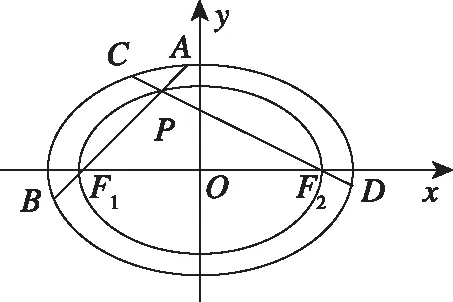
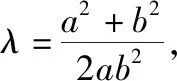
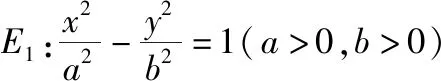
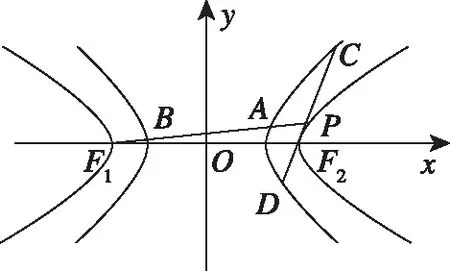
经过探究谁能总结探究得到的结论？在教师的引导下，学生经过思考、研究和交流，可以得到如下结论：对于两个椭圆、两个双曲线及一个椭圆和一个双曲线，满足第一个曲线的两个顶点A1，A2(焦点所在轴上的顶点)为第二个曲线的两个焦点F1，F2，P为第一个曲线上异于A1，A2的任一点，直线PF1和PF2与第一个曲线的交点分别为A，B和C，D.当第一个曲线为等轴双曲线或以第二个曲线的焦距为直径的圆时，存在常数λ，使得|AB|+|CD|=λ|AB|·|CD|恒成立.