求数列有关最值或值域的常用方法

四川

杜海洋

(作者单位：四川省成都经济技术开发区实验中学校)

数列是一种函数，所以函数求最值或值域的很多方法如配方法、数形结合、基本不等式、导数和单调性等同样适用于它，又由于数列是一种特殊的函数，在求最值或值域时，又表现出它的特殊性，有些特殊的方法如放缩法和夹逼法等也可用于数列.下面笔者通过近几年高考或各地模拟试题中出现的数列考查方法进行归类总结，以飨读者！

方法一、配方法

【例1】已知数列{an}的通项an=-2n+15，则其前n项和Sn取得最大值时n的值为

( )

A.1 B.7或8

C.8 D.7

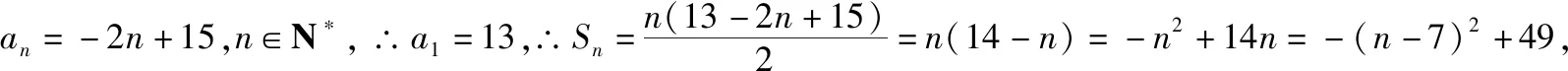
【例2】已知数列{an}是等差数列，a1<0，a8+a9>0，a8·a9<0.则使Sn>0的n的最小值为

( )

A.8 B.9

C.15 D.16

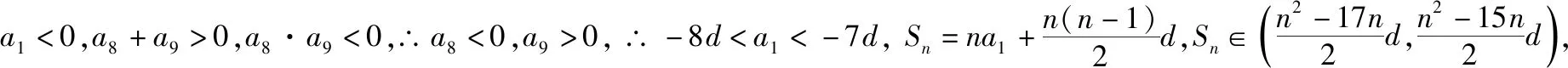
【点评】数列是一种特殊的函数，等差数列的前n项和可以看作是一个关于n的二次函数Sn=An2+Bn；等差数列{an}的通项公式可以看作是一个关于n的一次函数.一般等差数列求前n项的和的最小值或最大值常见的有两种方法：一是可以通过通项得出数列的单调性，如果单调递增，就求出负数最大的项，如果单调递减，就求出正数最小的项，再进一步求出前n项的和的最小值或最大值.二是通过求和公式转化为二次函数Sn=An2+Bn，再利用配方法进行求解，其中注意n只能取正整数.

方法二、数形结合法

【例3】设等差数列{an}的前n项和为Sn，已知a3=12,S12>0,S13<0.

(Ⅰ)求公差d的取值范围;

(Ⅱ)指出S1,S2,…,S12中哪一个值最大,并说明理由.

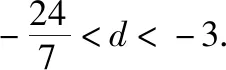
【点评】数列是一个特殊的函数，等差数列{an}的前n项和可以看作是一个关于n的二次函数Sn=An2+Bn，利用图象解答，其中要注意等差数列的前n项和不一定在抛物线的顶点取得最大(小)值，因为数列中的自变量n取正整数.若an+1=0，则Sn与Sn+1相等，且均为最值.

方法三、单调性法

【例4】已知数列{an}的前n项和为Sn，且Sn=2an-2.

(Ⅰ)求数列{an}的通项公式；

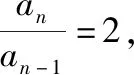
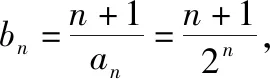
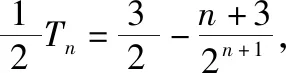
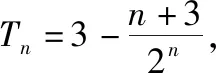
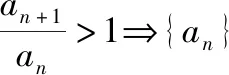
方法四、基本不等式法

( )

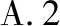
C.3 D.4

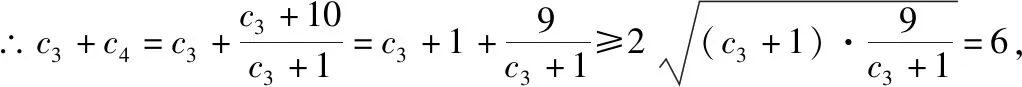
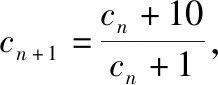
方法五、判别式法

【例6】若存在等比数列{an}，使得a1(a2+a3)=6a1-9，则公比q的最大值为

( )

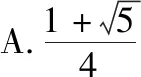
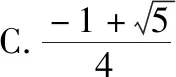
当q+q2=0时，易知q=-1，满足题意；

方法六、导数法

【例7】设等差数列{an}，{bn}的前n项之和分别为Sn，Tn.若对任意n∈N*有①(n+3)Sn=(3n+1)Tn；②an2+27≥λ·bn均恒成立，且存在n0∈N*，使得实数λ有最大值，则n0=

( )

A.6 B.5

C.4 D.3

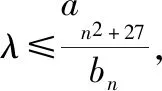
∴n∈N*时，f(5)取得最小值.则n0=4.故选C.

【点评】本题考查了等差数列的求和公式及其性质、利用导数研究其单调性.其中注意，第一，利用导数求数列的最值，不能直接求，必须先构造对应的函数，因为数列是离散型函数，不可导.第二，注意数列对应的函数的单调性和数列本身的单调性是有区别的，当数列的函数在(0，a)上单调递增，在(a,+∞)上单调递减时，数列不一定在最靠近x=a的地方取得最大值，必须把x=a附近的整数值代进去比较，才能找到最大值.所以一般利用导数求数列的最值要慎重.

方法七、其他方法

1.极限思想或者放缩法

( )

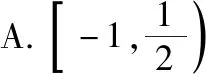
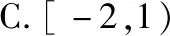
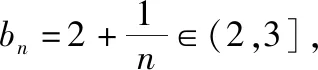
2.二项式的展开式

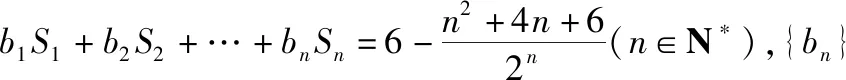
(Ⅰ)求数列{an}和{bn}的通项公式；

【解析】(Ⅰ)已知等差数列{an}的前n项和为Sn，a1=1，公差d≠0，且S1，S3，S9成等比数列，则(3+3d)2=9+36d，解得d=2，所以an=2n-1(n∈N*)，故Sn=n2.

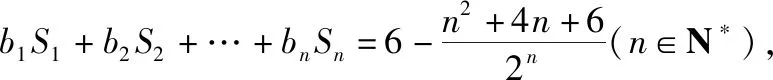
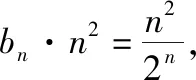
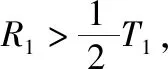
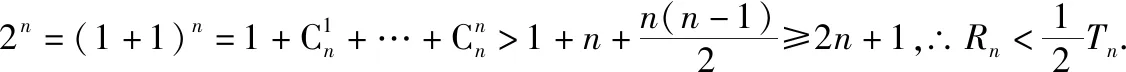
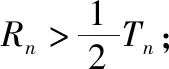
3.夹逼法

【例10】已知{an}是等差数列，Sn为{an}的前n项和，若a1=5，S4=8，则nSn的最大值为

( )

A.16 B.25

C.27 D.32

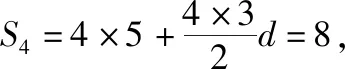
∵n是正整数，∴只有当n=4时，才满足不等式组，即当n=4时，nSn最大，最大值为42(6-4)=16×2=32，故选D.