立足课程标准 导向数学理解*——以近4年浙江省杭州市数学中考试题为例

(富阳区教育发展研究中心,浙江 杭州 311400)

2016年浙江省杭州市数学中考命题组提出“研究数学、专注教学、关心学生”的考查方向，杭州市数学中考试卷(以下简称“杭州卷”)连续4年践行初心，重视基础知识和概念内涵，关注问题解决的一般方法，指向数学素养.持续传递立足课标、理解数学的理念，形成了“重视基础知识，重视数学本质，导向核心素养培育”的特色.

1 重视基础知识

义务教育数学学科第三学段内容为数与代数、图形与几何、统计与概率这3个板块，不同的知识板块教学重点各有侧重，杭州卷立足课标，重视对3个板块基础知识和基本技能的考查.

1．1 运算能力

有理数教学是初中数学学习的起点.《义务教育数学课程标准(2011年版)》(以下简称《课标》)对有理数运算的要求：能比较有理数的大小……，掌握有理数的加、减、乘、除、乘方及简单的混合运算.可见，数的范围扩展到有理数以后，有理数的学习就是负数的学习，有理数运算的重点是负数参与的运算.如：

例1计算下列各式，值最小的是

( )

A．2×0+1-9 B．2+0×1-9

C．2+0-1×9 D．2+0+1-9

(2019年浙江省杭州市数学中考试题第1题)

先来看这个问题的设计立意：该题的运算对象是有理数，涉及的运算为有理数的加、减、乘，涉及有理数加法、减法、乘法的运算法则；是对运算程序的考查，同时注意到每一个计算结果都是负数，需要进一步对负数进行大小比较；很好地体现了《课标》对有理数的性质及运算的要求，区分出中小学阶段有理数教学的学习差异.

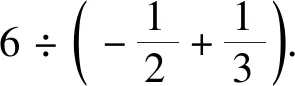
方方同学的计算过程如下：

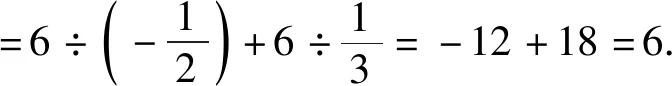
请你判断方方的计算过程是否正确，若不正确，请你给出正确的计算过程．

(2016年浙江省杭州市数学中考试题第17题)

该题用意深刻，括号内是小数减大数，体现了初中阶段有理数教学的基本要求.有理数的代数性质除了运算规律还有运算律，如何考查运算律是一个难题.本题巧妙地化解了这个难题，把乘法对加法的分配律巧妙地镶嵌在这个纠错运算中，要求学生充分理解分配律的适用范围和运算规律.

两个试题均质朴无华，考查的内容都是有理数的运算，试题给教学的启示是有理数教学需要明确其教学任务，即有理数的大小性质、有负数参与的运算以及运算律是教学的核心.有理数的运算本质上就是用运算律使运算更加合理、准确.

1.2 几何图形整体处理能力

平面几何主要研究几何量之间的数量关系和位置特征，最重要的是对称性、平行性和度量研究，其基本图形是等腰三角形、平行四边形和直角三角形.对称的本质是“保长”“保角”，平行性的本质是方向差.几何的根本在于度量，度量的工具在于面积公式、勾股定理和相似的性质.

第三学段《课标》要求：探索并理解平面图形的平移、旋转、轴对称…….下面看杭州卷的呈现方式：

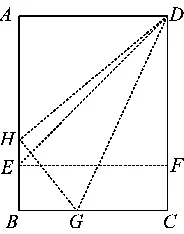
图1

例3如图1，折叠矩形纸片ABCD时，发现可以进行如下操作：1)把△ADE翻折，点A落在DC边上的点F处，折痕为DE，点E在AB边上；2)把纸片展开并铺平；3)把△CDG翻折，点C落在线段AE上的点H处，折痕为DG，点G在边BC上．若AB=AD+2，EH=1，则AD=______．

(2018年浙江省杭州市数学中考试题第16题)

这是一个折叠问题，折叠的本质是对称，通过对称可以实现等量关系的传递.矩形作为一个特殊的平行四边形，自身就具有丰富的对称性.以矩形为载体，把几何图形的对称性和度量结合考查，凸显命题人对几何本质的理解以及对《课标》的准确把握，题目不难但回味悠长.

1.3 数据分析和处理能力

《课标》要求：体验数据收集、处理、分析和推断的能力……，可见统计学习的核心目标是发展数据分析观念、数据分析的能力以及对统计对象数字特征的理解和运用能力.

统计研究往往是建立在数据背景下的研究，本质上是归纳法[1].初中阶段统计内容的学习更多的是关注学生数据处理观念的培养，让学生理解在不损失信息的前提下，对样本数据从不同的角度作出分析的意义，能用少量的信息还原总体特征.

例4点点同学对数据26，36，36，46，5■，52进行统计分析，发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是

( )

A．平均数 B．中位数

C．方差 D．标准差

(2019年浙江省杭州市数学中考试题第5题)

每一种统计量对一批数据的考查目标是不同的.中位数只与数据的位置有关，只受一组数据最为居中的一个(或两个)数大小的影响，只要数的位置不改变(也不增减数据)，只调整中位数前后的数据大小，这一组数据的中位数不会发生变化.

例5测试5位学生的“一分钟跳绳”成绩，得到5个各不相同的数据．在统计时，出现了一处错误：将最高成绩写得更高了．计算结果不受影响的是

( )

A．方差 B．标准差

C．中位数 D．平均数

(2018年浙江省杭州市数学中考试题第4题)

从统计的角度看，平均数(均值)和中位数都用来刻画一组数据的集中程度，在数据分布正态(对称)的情况下是一样的，但是数据分布偏态(不对称)的情况下，均值会出现偏差，中位数就需要承担刻画数据集中程度的作用.这个问题带来的启示：统计教学中需要帮助学生理解作为数据集中程度的指标，中位数与平均数相比有其独特的意义和价值，此题巧妙地诠释了中位数的意义.

例4和例5这两个中位数问题考的是数据处理的理解水平和基本观念，简洁灵动，高水平的题目根植于命题人深厚的数学水平.

例6某计算机程序第一次算得m个数据的平均数为x，第二次算得另外n个数据的平均数为y，则这m+n个数据的平均数等于______．

(2019年浙江省杭州市数学中考试题第12题)

表面上看，这是在考查加权平均数，但背后意义深远：随着科学的飞速发展、大数据时代的到来，统计越来越显示出重要性，以往的线性计算平均数的方式无法满足大数据处理的需要，计算科学发生了深刻变革，平行计算是新的处理数据的方式，其原理就是简简单单的加权平均数公式，该公式承载了统计功能的深刻变化，此题就是帮助教育者感受这一深刻变革.

2 体现目标层级

《课标》将知识与技能的描述划分为3个层级：了解(知道与模仿)、理解(独立操作)、掌握(应用与迁移)，每一目标层级对应不同的能力水平要求.

2.1 依据目标层级设定考查深度

概念教学的目标分为“了解、理解、掌握”等层级水平，命题的深度也分为了解、理解(掌握)、应用[2]，这是《课标》的要求.

史宁中老师曾经就“三角形内角和”谈过目标层级的理解.《课标》要求探索并掌握三角形内角和定理.了解：知道三角形内角和为180°；理解：还知道一个三角形不能有两个钝角、四边形内角和为360°；应用：知道三角形外角和为360°等等.

例7在△ABC中，若一个内角等于另两个内角的差，则

( )

A．必有一个内角等于30°

B．必有一个内角等于45°

C．必有一个内角等于60°

D．必有一个内角等于90°

(2019年浙江省杭州市数学中考试题第7题)

这个问题显然是在考查“三角形内角和”，依据《课标》和史宁中老师的分析来看，这个考题恰到好处地体现了目标层级的要求.

2．2 依据目标层级设置题目类型

《课标》对应用题的要求：能根据具体问题中的数量关系列出方程，体会方程是刻画现实世界数量关系的有效模型.

例8已知九年级某班30位学生种树72棵，男生每人种3棵树，女生每人种两棵树．设男生有x人，则

( )

A．2x+3(72-x)=30

B．3x+2(72-x)=30

C．2x+3(30-x)=72

D．3x+2(30-x)=72

(2019年浙江省杭州市数学中考试题第4题)

根据等量关系抽象出方程模型，起始于七年级一元一次方程内容，是体验数学思想方法的重要起点.注意到近4年杭州卷的应用题都是考查抽象建模，没有繁杂的类型和解法，体现《课标》要求，引领教学回归根本，大工不巧，大巧若拙.

3 回归内容本质

杭州卷立足思想方法和数学理解，理性回归知识本质，不超纲不越界，章法清楚不遮掩，直指素养.

3.1 函数问题去解析化

依据《课标》要求，杭州卷对函数的考查聚焦解析式、图像、性质.利用图像的位置特征、图像的几何特征、函数性质的代数刻画以及函数与方程、不等式的内在联系研究问题，是函数学习和考查的重点.

例9设二次函数y=(x-x1)(x-x2)(其中x1，x2是实数)．

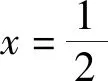
2)写出二次函数图像的对称轴，并求该函数的最小值(用含x1，x2的代数式表示)．

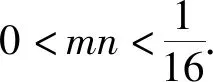
(2019年浙江省杭州市数学中考试题第22题)

此题起点于函数解析式，落脚于函数单调性，可以借助图像，也可以借助代数推理解决问题，凸显了二次函数的研究本质以及数形结合、分类讨论、化归归纳、函数方程等重要的数学思想方法.

例10设二次函数y=ax2+bx-(a+b)(其中a，b是常数，a≠0)．

1)判断该二次函数图像与x轴的交点的个数，说明理由；

2)若该二次函数图像经过A(-1，4)，B(0，-1)，C(1，1)这3个点中的其中两个点，求该二次函数的表达式；

3)若a+b<0，点P(2，m)(其中m>0)在该二次函数图像上，求证：a>0．

(2018年浙江省杭州市数学中考试题第22题)

这个问题提供给学生的解决途径非常宽泛，既涉及二次函数的解析式、图像、性质，又巧妙地将函数、方程、不等式问题加以关联，体现《课标》要求.

聚焦函数，不掺杂几何问题，回归知识根本属性，这是杭州卷考查函数问题的方式.

3.2 三角函数去函数化

初中阶段三角函数不是作为函数来研究的，《课标》将三角函数知识置于相似三角形板块：知道30°，45°，60°的三角函数值……能用锐角三角函数解直角三角形，能用相关知识解决一些简单的实际问题.

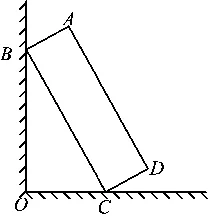
图2

初中阶段三角函数的本质是直角三角形的边角比，用来解直角三角形，并不涉及“函数”，之所以称为“三角函数”，实际上是概念泛化.高中解斜三角形的学习方法与初中完全类似，本质是边与角的更一般关系的表示，这些内容都属于古希腊托勒密时代的“三角学”，并非现代意义的三角函数.

例11如图2，一块矩形木板ABCD斜靠在墙边(OC⊥OB，点A，B，C，D，O在同一平面内)．已知AB=a，AD=b，∠BCO=x，则点A到OC的距离等于

( )

A．asinx+bsinxB．acosx+bcosx

C．asinx+bcosxD．acosx+bsinx

(2019年浙江省杭州市数学中考试题第9题)

与其说这是一个三角函数问题，不如说这是一个几何问题，三角函数起到了转化“直角三角形中的边角关系”的作用，不超纲不越位，恰如其分.

3．3 几何问题去解析化

依据《课标》可知，“发展空间观念，几何直观、推理能力”是初中平面几何能力的培养核心要求.按照《课标》划分，解析几何属于高中阶段的学习内容，杭州卷坚持图形性质、图形变化等基础问题研究，关注研究的基本方法.

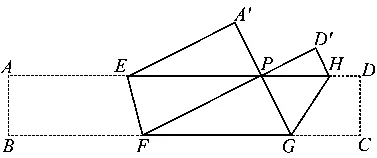
图3

例12如图3，把某矩形纸片ABCD沿EF，GH折叠(点E，H在边AD上，点F，G在边BC上)，使点B和点C落在边AD上同一点P处，点A的对称点为A′，点D的对称点为D′．若∠FPG=90°，△A′EP的面积为4，△D′PH的面积为1，则矩形ABCD的面积等于______．

(2019年浙江省杭州市数学中考试题第16题)

这是基于轴对称视角的折叠问题，既可以直接使用特殊三角形，也可以构造全等三角形，还可以利用相似三角形等各种图形的性质解决问题.涉及到勾股定理、三角形面积等基础知识，无需动用解析法，不适合采用解析法.

4 导向数学理解

4.1 理解数学是根本

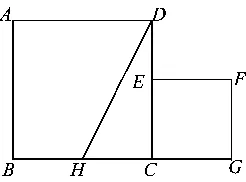
图4

例13如图4，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在边DC上，点G在BC的延长线上．设以线段AD和DE为邻边的矩形的面积为S2，且S1=S2．

1)求线段CE的长;

2)若点H为边BC的中点，联结HD，求证：HD=HG．

(2019年浙江省杭州市数学中考试题第21题)

从问题解决的视角看，此题涵盖了正方形、直角三角形、等腰三角形等特殊图形，用勾股定理、等积变形等基本计算，考查的是核心知识及方法.

从命题的视角看，此题中度量是本质，所呈现的是简单度量，背后蕴含着找线段黄金分割点的构图法：点E是线段CD的黄金分割点，线段CE的长度是方程x2+x-1=0的一个实数根.学生无需懂得背后深奥的原理，只需要根据题意，利用方程刻画出图形间所具有的等量关系即可解决问题，举重若轻源于深厚的理解.

4.2 问题解决的一般观念是追求

杭州卷注重问题一般化的研究，追求解决问题的一般思路，在代数、几何甚至统计问题中多有体现.

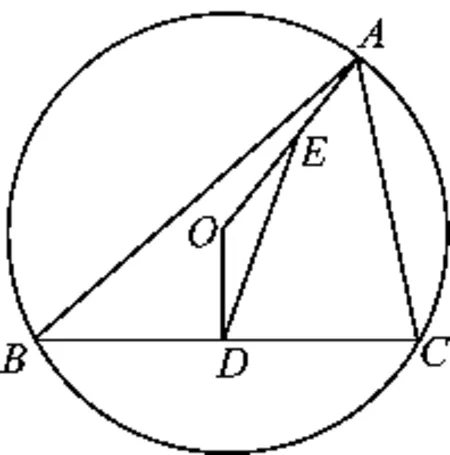
图5

例14如图5，已知锐角△ABC内接于⊙O，OD⊥BC于点D，联结OA．

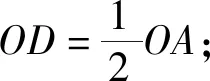
2)点E在线段OA上，OE=OD，联结DE，设∠ABC=m∠OED，∠ACB=n∠OED(其中m，n是正数)．若∠ABC<∠ACB，求证：m-n+2=0．

(2019年浙江省杭州市数学中考试题第23题)

问题解决的一般思路体现在两个方面：其一，在圆的相关性质中，圆周角的性质是圆所特有的，此题第2)小题若借助圆周角解决则会非常简洁，堪称圆周角问题的极致;其二，第2)小题的解决回避了特殊的度数，将问题上升到更为一般的层面，根据变化过程中的不变性和特殊性，找出更为一般的结论.正如著名数学家陈省身教授1980年在北京大学讲学时提到一个观点：数学不是罗列更多的现象，也不是追求更妙的技巧，而是要从更普遍的、更一般的角度寻求规律和答案.

5 思考与启迪

中考卷不仅具有选拔区分功能，更是一种教学导向，可以看出杭州卷对教学的引领：

5.1 以生为本

杭州卷的考查方式直接减少学生不必要的负担，将师生重新带回课堂，寻求对数学本质的理解.“关心学生”,这是杭州市初中教师在2016年提出的理念，时至今日，杭州卷用行动表明关心学生的初心未改.

5.2 引领教学

考查学生的数学理解水平，就是在考查教师的理解水平，只有教师具有充分数学实质性结构知识，才能有效地引导学生用数学的眼光看世界[3].杭州卷更深远的思考在于引领教师研究数学，理解数学.在杭州卷的努力之下，命题回归数学本源，用一般观念指导教学等理念已经逐步得到认可.

5.3 数学育人

真正的教育应该是以学生的发展为本，这是最核心的教育理念.学生面对更高学段的学习，理解知识内部原理，“会学习”是根本.杭州卷用行动对接课程理念，用心良苦，展现了数学育人的基本范式.