浅析2019年浙江省数学高考压轴题*
(湖州市第二中学,浙江 湖州 313000)
(湖州市教科研中心,浙江 湖州 313000)
继2018年浙江省数学高考更换压轴大题题型之后,2019年亦如外界所“期待”的,依旧以导数题压轴,这凸显了函数在数学高考中的重要地位.而本道压轴题背景公平熟悉,试题表述简洁精准,设问由浅入深,梯度明显.而试题的设计返璞归真,着重考查“逻辑推理”与“数学运算”等重要的学科核心素养.纵向对比2018年数学高考压轴大题,笔者认为:2019年压轴大题除了传承“浙江卷”所一贯重视的挖掘数学本质之外,对学生的推理、归纳猜想、运算技巧等综合数学能力的要求更高了.下面笔者从试题的“解法”“思想”“素养”等多方面解读这道压轴好题,望读者批评指正.
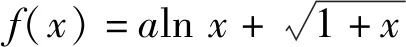
(2019年浙江省数学高考试题第22题)
1 “庖丁解牛”,说解法
1.1 单调性求解,波澜不惊
这里是本题的第一道“关卡”.函数求导并通分之后,导函数的“正负号”并不直观.而接下来的处理方式通常有两类:
2(t2-1)-3t=(t-2)(2t+1),
于是当t>2,即x∈(3,+∞)时,函数单调递增;当1 2)利用平方差公式对分子进行有理化,即 总之,求导、通分、因式分解都是求单调区间的常规套路,只不过细节处理上略有不同. 再分析第2)小题.粗看这是一个典型的“全称命题求参数范围”问题,然而常规方法“参变分离”无法实现,“分类讨论”便是唯一选择.但讨论方向又头绪繁杂,令人望而却步,于是想到从原题的必要性条件入手,“特殊点代入”能简化讨论类别. 面对多元问题,如何化繁就简、排除干扰是解题关键所在,这亦是本题的又一道“关卡”.著名数学家波利亚曾指出:“当原问题看来不可解时,人类的高明之处就在于会迂回地绕过不能直接克服的障碍,就在于能想出某个恰当的辅助问题”.于是,可以利用换元等函数构造工具达到化繁就简、排除干扰、简化计算的目的. 从而 而 综合以上解法,第2)小题的必要性可取特值点,蕴含着从特殊到一般的数学思想,而后续的函数不等式证明问题中,涉及换元思想、主元转换、有理化计算、隐零点设法,手段多元,平凡中蕴含着美丽.然而能将众多思想方法融为一体,着实不易,以下笔者溯源真题,例说部分精彩实用的数学思想方法. 1)略; 2)若f(x)在区间[1,4]上的最小值为8,求a的值. (2014年江西省数学高考文科试题第18题) 图1 例3已知函数f(x) =ln(x+1)-x,g(x)=xlnx. 1)略; (2004年全国数学高考卷Ⅱ理科试题第22题) 又b>a,得 h(b)>h(a)=0. 1)若f(x)在x=x1,x2(其中x1≠x2)处的导数相等,证明:f(x1)+f(x2)>8-8ln 2; 2)略. (2018年浙江省数学高考试题第22题) 化简得 从而g(t)在(16,+∞)上单调递增,于是 g(t)>g(16) , 即 f(x1)+f(x2)>8-8ln 2. 由以上例子我们发现,这些巧妙的数学方法在过去的高考真题中经常出现,然而2019年浙江卷的压轴大题可谓“集大成者”,足见命题者的良苦用心. 《普通高中数学课程标准(2017年版)》(以下简称《新课标》)提出了数学教学的终极目标:要让学习者会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界.其中“数学的思维”主要指向的是逻辑推理与数学运算.而当我们重新回顾、品味本道压轴大题时,发现它正是侧重于考查这两大核心素养的. 波利亚的数学解题思想中包含这样一个基本观点:数学具有双重性,即数学既是演绎科学,又是归纳科学.而例1第2)小题解答中,“必要性探路,先猜后证”充分体现了“归纳”推理;在证明过程中“主元转换,分类讨论”又需要严谨扎实的“演绎”功底.事实上,恒成立取点是有经验成分的,可以理解为非理性的直觉作用.因此在平时解题教学中,教师应鼓励并放手让学生大胆猜想及严谨论证,体悟数学的本质.正如东北师大史宁中教授所说的“学生逻辑推理素养的形成和发展,在本质上,不是靠教师‘教’出来的,而是靠学生‘悟’出来的”[2]. 《新课标》就数学运算核心素养分成3个递进的层次. 笔者认为,一道好的压轴大题应该为不同基础、不同能力水平的考生都提供适当相应的思考空间,体现较好的区分度.而例1对于数学运算素养的考查便是根据不同水平层次,逐步递进的. 首先,第1)小题求解“函数的单调区间”,是学生熟悉的运算对象.而求导、通分、因式分解也都是此类问题常见的运算方向,此乃“水平一”. 其次,第2)小题中能利用换元、变换主元等运算工具,将原本复杂且“无从下手”的函数表达式转换成熟悉可控的二次函数(或对勾函数),此乃“水平二”. 最后,以函数极值点为临界值,分类讨论.若要完成这两段区间中的证明过程,则需要多次用到构造函数、求导、换元、有理化、放缩等种种计算技巧,达到了“水平三”. 事实上,数学运算本身是一种演绎推理.“计算”与“推理”你中有我、我中有你,相辅相成.正如例1中,“推理”指明了“计算”的方向;而通过“计算”反过来又验证了“推理”的正确性[3]. 结束语每年高考结束后总能留下许多精彩有趣的试题,值得我们去欣赏、探究.如果把高考试题比作夏日里盛开的一池荷花,那么高考压轴大题往往是那最娇艳芬芳的一朵,它瓣瓣生香,又形成一个完美的整体,令人回味无穷!1.2 不完全归纳,先猜后证
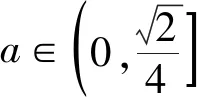
1.3 主元转换,换元辅助



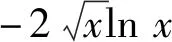
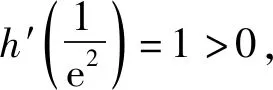
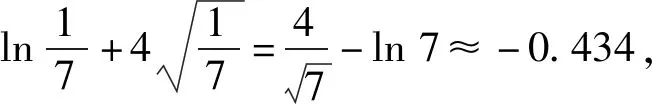

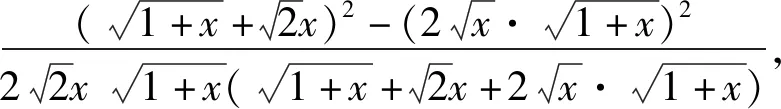
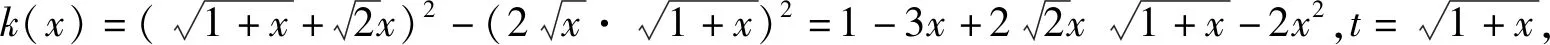
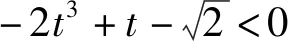
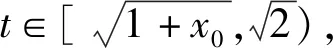
2 溯源真题,寻方法
2.1 简化分类的工具——必要性先行
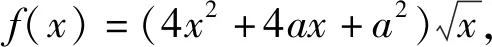
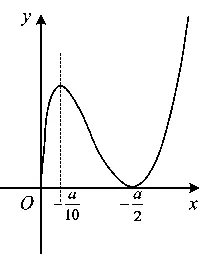

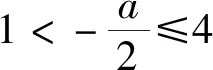
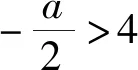
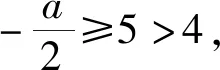
2.2 逆向思维的体现——主元构造
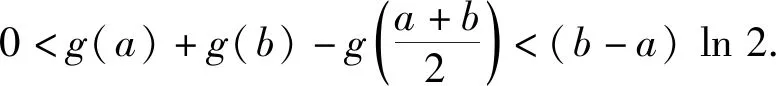


2.3 优化计算的法宝——换元构造
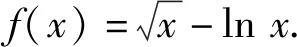
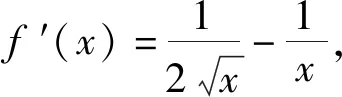

3 逻辑运算,展素养
3.1 演绎归纳,相辅相成
3.2 运算水平,层层递进

