找点搭线构面 教会学生选择*——一道高三模考试题的解法剖析、变式和反思

(金陵中学,江苏 南京 210005)

(南京市第十二中学,江苏 南京 210011)

学生是教学实施的主要对象，是学习材料的实践者.学生的学习过程，其实是一连串的选择活动，从学习目标、学习方式到学习手段，无一不是选择的结果；从“学什么”到“怎么学”也无一不是选择的过程[1]，因此，学生学习的选择能力应该受到重视.数学选择能力其实就是数学学习能力的直接体现.

高三数学教学要以发展学生的学科素养为导向，找准“切入点”(核心知识点、关键点、疑难点等)，搭建重要“转化线”(知识线、方法线、思想线等)，连点成线，构建系统“结构面”，将知识进行整合，方法进行比较，从整体上促进学生对问题本质的理解，进而培养学生积极和精准的选择能力，更要关注学生创造性的选择力.教师要引导和帮助学生学会选择，贴近学生的想法，为学生创建良好的学习情境，不断满足学生的学习需求，促进每一位学生积极主动地思考问题，让学生学“通”和学“透”，从而建立一种良好的“教”与“学”的循环体，优化课堂教学结构，提高课堂教学效益.

1 提出问题

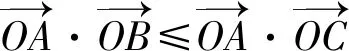
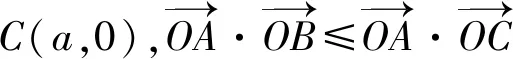
下面，笔者通过对题目解法的剖析和选择，谈谈在这方面的实践和思考，与同行分享.

2 解法探究

数学解题的关键点是探寻解题的“题眼”，转化是思维的主线，即将复杂问题简单化、将陌生问题熟悉化、将运动问题静止化、将隐性问题显性化等，转化目标的分析和转化方向的选择对问题的求解至关重要.

2.1 向量分析，选择“投影”

解法1由f(x)=x3-a2x(其中a>0,x≥0)，得

f′(x)=3x2-a2,

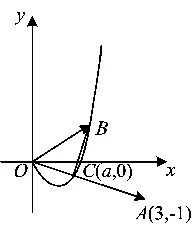
图1

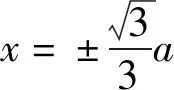
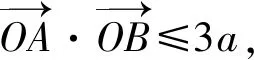
即

f′(x0)=3，

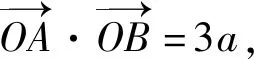
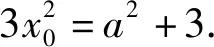
(1)

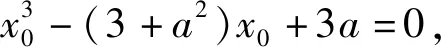
(2)

进而得

2.2 图形分析，选择“切线”

3x-y≤3a，

即x3≥(3+a2)x-3a在[0,+∞)上恒成立.令g(x)=x3，t(x)=(3+a2)x-3a，易知g(a)=t(a)，即两个函数图像都过点D(a,a3)(如图2)，且当x≠a时函数g(x)的图像恒在t(x)的上方，从而直线y=(3+a2)x-3a为曲线y=x3在点D处的切线，得

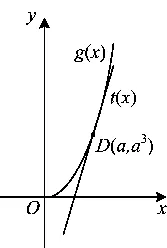
图2

即

3a2=a2+3(其中a>0)，

故

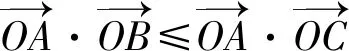
2.3 导数分析，选择“最值”

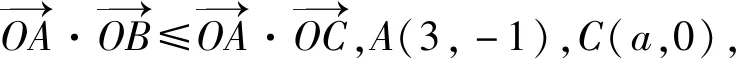
又g(a)=0，得

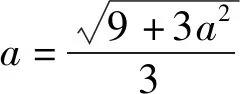
式(15)中Resmax，Cmax，Pmax为目标芯片可提供的相关代价函数的最大数值，用于归一化各项代价函数取值，参数w1,w2,w3为各项代价函数权值，可以根据实际需要进行赋值.

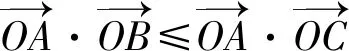
2.4 定点分析，选择“降次”

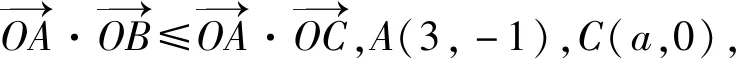
令g(x)=x2+ax-3，易知g(x)在区间[a,+∞)上单调递增，从而

g(x)min≥0，

即

g(a)≥0，

当x∈[0,a]时，x2+ax-2≤0恒成立，令g(x)=x2+ax-3，易知g(x)在区间(0,a]上单调递增，从而

g(x)max≤0，

g(a)≤0，

得

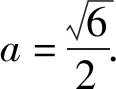
评注对于x3-(3+a2)x+3a≥0在[0,+∞)上恒成立问题，也可以选择先将其不等式左边的整式因式分解，再借助于分类讨论，利用夹逼法求a的值.因式分解是该解法求解的难点，由点C(a,0)的暗示，易知x-a是它的一个因式，于是达到了降次的目的，难点得以突破.该种方法更能考查学生的代数功底以及数学逻辑推理、数学运算等素养.

3 变式探究

( )

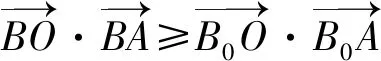
A.B0M⊥OA

B.B0M=OA

D.B0M⊥l(其中l是函数图像过点B0的切线)

例2依然沿着转化的主线，借助化动为静的思想设计题目，供学有余力的学生课后探究.该变式题主要以向量数量积知识为背景，利用极化恒等式方法求解是首选.通过变式题丰富复习内容、辐射解题方法、拓展解题视域、优化思维品质、感悟解题亮点、揭示问题本质、选择最佳路径求解问题.变式要在原有的基础上有所创新，要让学生在变式中获得新知识、新方法、新思路、新体验.

例3下列4个正方体图形中，A,B为正方体的两个顶点，M,N,P为正方体的顶点或为其所在棱的中点，能得出AB∥平面MNP的图形的序号是______.

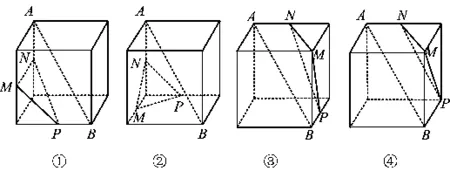
图3

例3考查的核心知识点是直线与平面平行的判断(知识点定位要精准)，要说明AB∥平面MNP，关键是要在平面MNP中找到某一条直线与AB平行，或者构造经过直线AB的平面与平面MNP平行，或者利用空间向量知识求解等.通过改变平面MNP的位置，让学生感受数学知识的发生过程，揭示问题的本质，丰富学生的选择路径,唤醒学生的选择意思,培养学生的选择能力.既然存在多种解题路径，那么学生会作出怎样的选择？教师要引领学生分析这是一个什么类型的问题？含有哪些条件？能否挖掘其中的隐含条件？条件和结论之间有何关联？可以选择什么路径？在交流的过程中，让学生探讨问题的本质，厘清知识的来龙去脉，建立知识之间的联系，从而掌握解题之法(问题求解的切入点)、积累解题经验(问题解决的转化线)、领悟解题之道(构建系统的结构面)，在各种解题途径中作出合理和准确的选择，少走弯路.

4 教学反思

4.1 找准“切入”点，教会学生选择

解题思路的获得就是要找准“切入”点，其实就是要做好理解题意和找出已知数据和未知量之间的联系，切入点的选择正确与否直接关系到解题的成败.教会学生如何选择解题的“切入”点，它具有什么样的特征，如何识别这种特征，才能为解题做好铺垫.

4.2 搭好“转化”线，教会学生选择

只有做好转化工作，才能顺利地实施解题计划.转化是解题的利器，转化方向的选择直接影响到解题的繁简程度，比如，对x3≥(3+a2)x-3a的转化可以选择多种形式，在讲评时教师要认真设计教什么和怎么教、用什么样的方式呈现给学生才能引起学生的共鸣，让所有的学生都能沿着“转化”线路思考问题，在试题的讲评中都会有所获、有所感悟.在问题的转化过程中应加强师生间的思维对话，不但要学生掌握解题方法，更要重视训练学生的思维品质.多视角审视一题多解、一题多变、一题多思、一题多讲，比如例3，通过问题的解决达到巩固基础知识、探索解题规律、形成解题技能、优化思维方法、揭示问题本质等目的[2].

4.3 构建“结构”面，教会学生选择

任何一个可解决的数学问题，其结构(个性特征)与解决它的方法之间必然存在着其和谐的、令人赏心悦目的内在联系[3].数学知识间是相互关联的，具有较强的连续性和整体性，教师在进行解题教学时不能只停留在对解法的分析，而应该告诉每种方法是如何想到的、为什么这么想；要立足于整个知识结构，进行一个系统剖析，从中提炼解题方法，感悟数学思想.通过变式题拓展学生的思维，让学生对涉及到的知识点和解题方法再总结和再反思，能从全局的角度思考问题，为解题提供更多的和可供选择的思维视角.只有建立知识点间的联系，才能理解问题的本质，将问题表征到位；只有将各种方法比较和反思，才能为解题作出灵活选择，提高解题效益；只有重视问题引领，才会达到“教”与“学”的一种高度融合，提高高三复习效益.

数学解题教学，教师不仅仅限于教给学生解题方法，而且更应该教会学生方法的选择能力，让学生学会思维，理解问题本质，从而实现“教师教得有效、学生学得高效、成绩出得显效”.