明素养导向 促深度学习*——2019年全国数学高考“概率统计”试题评析与教学启示

(宣城中学,安徽 宣城 242000)

概率与统计是近代数学的重要分支，是高考必考的内容之一，常以选择题、填空题、解答题的形式出现.掌握这类考题的命题规律，有助于提高高三复习的针对性、实效性.笔者以2019年全国数学高考中的概率统计试题为载体，对高考试题进行了深入思考，并探求高中概率统计的教学对策，以飨读者.

1 素养导向下的试题评析

高考试题命制已由重能力考查转到重素养导向：考查目标从常规性的问题解决技能到创造性的探究能力；考查情境从学科知识化到真实情境化；试题命制从单一知识点到复合知识点[1].为了更好地进行高三复习，笔者认真研究了2019年高考概率统计试题，希望能够对大家有所启示.

1.1 注重基础性，考查数学抽象素养

素养导向下的高考命题注重基础性.能力立意、素养导航是数学高考命题的基本原则，而数学基础知识是考查数学能力、数学素养的载体，因此注重基础性是2019年数学高考试题的特点之一.对于概率与统计，主要考查概率与统计的基本知识、基本思想和基本应用.

例1演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分.7个有效评分与9个原始评分相比，不变的数字特征是______.

A.中位数 B．平均数 C．方差 D．极差

(2019年全国数学高考卷Ⅱ理科试题第5题)

点评去掉1个最高分、1个最低分，平均数、方差、极差都可能发生变化，但中位数不变.本题以考生熟悉的演讲比赛中的评分为背景，考查样本数据的数字特征，考查学生是否弄清“中位数”“平均数”“方差”“极差”等基本概念，是否能从变化中抽象出不变来，考查了学生的数学抽象素养.

例2甲、乙两队进行篮球决赛，采取七场四胜制(当一队赢得四场胜利时，该队获胜，决赛结束).根据前期比赛成绩，甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6，客场取胜的概率为0.5，且各场比赛结果相互独立，则甲队以4∶ 1获胜的概率是______.

(2019年全国数学高考卷Ⅰ理科试题第15题)

点评本题以生活中的篮球比赛为情境，考查考生将实际问题转化为独立事件的概率计算，考查数学基本思想.根据比赛规则，甲队最终以4∶ 1取胜，说明前四场输一场，第五场甲赢.由于前四场安排依次为“主主客客”，采用分类与整合的思想，分为主场输一场或客场输一场，利用独立事件的概率公式计算得到结果.

纵观2019年的概率统计高考题可以看出，不管是选择题还是填空题、解答题，考查的内容都很好地体现了基础性.如全国数学高考卷Ⅰ文科第6题考查了抽样方法中的系统抽样，江苏省数学高考试题第5题考查了方差计算.通过对概率统计核心概念、基本思想的考查，增强考查内容的基础性.同时使学生牢固掌握解决问题的基本方法和工具，为学科核心素养的提升打牢基础.

1.2 突出情境性，考查数学建模素养

素养导向下的高考命题突出情境性.数学源于实际生活，概率与统计是一门专门研究偶然现象统计规律性的学科，有着广泛的应用背景.2019年的数学高考概率与统计命题把握时代的脉搏，设置真实的问题情境，设计出了情境鲜活、时代气息浓厚的精彩题目.

例3我国高铁发展迅速，技术先进.经统计，在经停某站的高铁列车中，有10个车次的正点率为0.97，有20个车次的正点率为0.98，有10个车次的正点率为0.99，则经停该站高铁列车所有车次的平均正点率的估计值为______.

(2019年全国数学高考卷Ⅱ文科试题第13题)

点评本题构思精妙，以我国高铁发展情况为情境，考查估计值，具有极强的情境性.试题既关注社会发展的时代特征，又展示中国先进的高铁技术，着重体现数学的应用价值.

同样，2019年全国数学高考卷Ⅰ理科第21题以科技试验为背景，由概率值解释试验方案的合理性；2019年北京市数学高考卷理科第17题以支付方式相关的调查为背景，突出了情境性，体现了概率统计在社会生活中的应用，同时引导学生从数学的角度分析社会现象，发展学生的数学建模素养.

1.3 体现文化性，考查数学文化素养

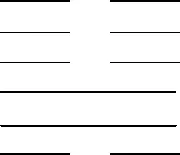
图1

素养导向下的高考命题体现文化性.无论全国卷，还是自主命题的地方卷，近几年均出现了以数学文化为背景的试题，渗透了数学文化，2019年也不例外.文化性继续成为高考数学的命题特色.

例4我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“——”和阴爻“— —”，图1就是一重卦.在所有重卦中随机取一重卦，则该重卦恰有3个阳爻的概率是______.

(2019年全国数学高考卷Ⅰ理科试题第6题)

点评本题以古代典籍《周易》为依托来命制数学文化背景试题，体现了东方数学的特点.解答本题有两种思路：可应用古典概型二项分布模型和组合知识求解概率，解决问题；也可以建立数学模型，并给予结果解释或赋予实际意义.

不仅是2019年全国数学高考卷Ⅰ理科第6题，纵览2019年的数学高考试题，很多试题都以优秀的中国传统文化为题材，通过高考命题让学生感受数学文化魅力，引导学生提高数学文化素养、传承民族精神、树立文化自信.

1.4 强化创新性，考查数学数据分析素养

素养导向下的高考命题强化创新性.概率统计试题强化创新性，将概率统计知识与其他知识相融合，如数列、导数、函数最值等，突出对新增内容的考查力度，这正是新课标高考的体现，也是高考命题的趋势.

例5为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验.试验方案如下：每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠，随机选一只施以甲药，另一只施以乙药.一轮的治疗结果得出后，再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效.为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得-1分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得-1分；若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X.

1)求X的分布列.

2)若甲药、乙药在试验开始时都赋予4分，pi(其中i=0,1,…，8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率,则p0=0，p8=1,pi=api-1+bpi+cpi+1(其中i=1,2,…,7),且a=P(X=-1)，b=P(X=0)，c=P(X=1)．假设α=0.5，β=0.8．

①证明：{pi+1-pi}(其中i=0,1,2,…,7)为等比数列；

②求p4，并根据p4的值解释这种试验方案的合理性.

(2019年全国数学高考卷Ⅰ理科试题第21题)

点评本题将概率统计作为压轴题，具有创新性，要求学生能够熟练掌握离散型随机变量的分布列的求解、由数列的递推关系证明等比数列的方法、由累加法求数列项的方法，对学生分析和解决问题的能力要求较高.求解离散型随机变量的分布列考查学生的运算素养，由递推关系证明{pi+1-pi}(其中i=0,1,2,…,7)为等比数列，求p4考查学生的逻辑推理素养和数据运算素养.

本题将概率与数列融合，综合性较强，题设新颖.这样命题不仅突出了学生对知识进行迁移以解决问题的能力的考查，更有助于考查学生的创新意识和数学素养，值得大家关注.

《普通高中数学课程标准(2017年版)》(以下简称《新课标》)指出，命题应依据学业质量标准和课程内容，注重对学生数学学科核心素养的考查，要充分考虑对教学的积极引导作用[2].概率统计问题是近几年高考的热点题型，以上笔者通过简析2019年全国数学高考试题中有关概率统计方面的试题，意在揭示该知识点的命题规律，分析命题方向，透视命题信息，引导教学活动.

2 基于深度学习的复习建议

培养和发展数学核心素养是《新课标》的明确要求，而“深度学习”是一种新的思维方式，是发展学生数学核心素养的主要方法和重要手段.为了科学、高效地组织好高三复习，促进学生深度学习，让核心素养生根，下面笔者谈谈如何利用教材进行概率统计知识点的探究式教学，希望能为广大中学数学教师提供参考.

2.1 依纲据本，建构基础知识体系

“依纲据本，建构基础知识体系”是促进学生深度学习、落实数学核心素养的良好载体.对概率统计基础知识的理解和掌握，对促进学生深度学习、发展数学核心素养发挥着关键作用，因此历年高考数学试题全面覆盖概率统计的各项内容.实际上，关于概率与统计问题的求解，只要抓住基本概念、基本理论和基本公式，还是比较容易处理的.

如2019年全国数学高考卷Ⅱ理科第5题考查了基本概念“中位数”“平均数”“方差”“极差”，而概念源自教材，教材是高考试题的重要知识载体.只要掌握了概率统计的基础知识(图2和图3)，不需要使用特殊的技巧就可以顺利地得出答案.

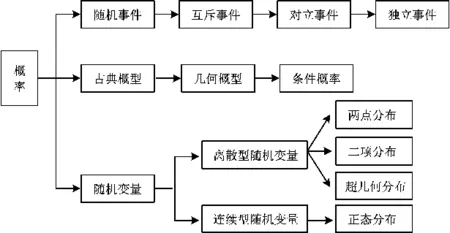
图2

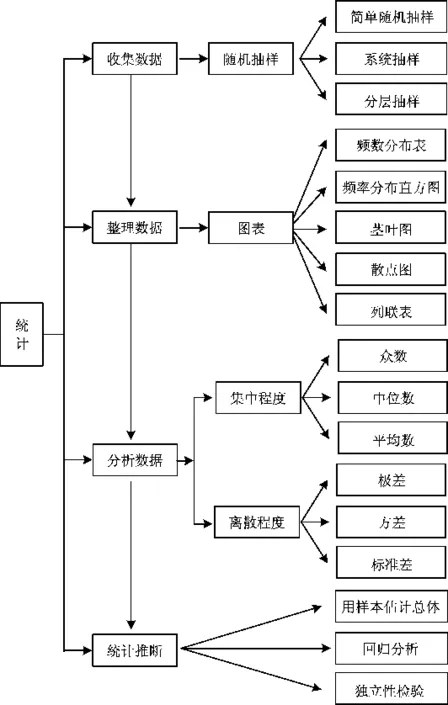
图3

因此，在概率统计的复习备考中，一定要引导学生回归教材，吃透教材，注重剖析基本概念，依纲据本，建构基础知识体系.

2.2 抓源固法，提炼基本数学思想

“抓源固法,提炼基本数学思想”是促进学生深度学习、提升数学核心素养的有力抓手.数学是思维的体操，考试大纲明确要求“对数学思想方法的考查是数学知识在更高层次上的抽象和概括”，对数学思想方法的考查历来是高考数学考查的重中之重，这表明比“刷题”更重要的是提炼数学思想.仔细研究发现概率统计试题体现了丰富的数学思想方法，如分类整合、逆向思维等，解题中如果我们能恰当选择数学思想方法，问题就比较容易解决.

高考试题把社会生活引入到试题中，增加试题情境，其实隐含考查的却是相关的数学思想，如2019年全国数学高考卷Ⅰ理科第15题对分类整合的数学思想进行了全面考查，2019年全国数学高考卷Ⅰ理科第21题考查了概率思想，2019年北京市数学高考理科第17题考查了统计推断思想.考生用相关的思想、方法去探究，就可以形成有意义的结论.因此，在复习备考中应注意引导学生抓源固法，提炼基本数学思想，以便提高解题速度.

2.3 引经据典，渗透数学文化精神

“引经据典，渗透数学文化精神”是促进学生深度学习、发展数学核心素养的有效依托.高考试题把中国传统文化引入到试题中，将数学文化与考查学生的运算求解、抽象概括、推理论证等能力和培养数据分析、数学抽象、数学建模等素养结合起来.

如2019年全国数学高考卷Ⅰ理科第6题以古代典籍《周易》为背景，只要抓住了统计与概率的基本模型(二项分布模型)，就能化繁为简，从而解决问题.此题较为简单，但它的意义和价值实际上已远远超出了试题本身，能激发考生学习热爱数学文化，积极主动地了解中国古代的数学成就.因此，在复习备考中，我们要挖掘课本中众多专题的丰富文化背景，引经据典，借助数学文化突破教学难点，从而渗透数学文化.

2.4 创情设问，聚焦数学核心素养

“创情设问，聚焦数学核心素养”是促进学生深度学习、发展数学核心素养的重要途径.通过对2019年全国数学高考概率统计试题的统计分析，笔者发现命制概率统计高考试题一般都将问题设置在一定情境中来考查学生的数学核心素养.

如2019年全国数学高考卷Ⅰ理科第21题求解离散型随机变量的分布列，考查学生的运算素养，考查学生的逻辑推理素养和数据运算素养；2019年全国数学高考卷Ⅱ理科第18题求事件“X=4且甲获胜”的概率，考查学生的逻辑推理素养和数学运算素养；2019年北京市数学高考理科第17题由表格分析数据，从而得到学生上个月两种支付方式都使用的概率，考查学生的数据分析素养，运算求解得到随机变量X的分布列和数学期望，考查学生的数学运算素养.

既然高考命题会创情设问激发学生的独立思考，那么，在高三阶段的概率统计复习备考中，我们就要十分重视创设合适的教学情境，聚焦数学核心素养，培养学生从数学的角度去发现问题、研究问题，感悟数学的思想，积累数学思维的经验[3].

总之，无论是在日常数学学习中，还是在高三的复习备考中，我们都不要沉溺于题海战术，更不要热衷于押题猜宝，而要善于在适量而科学的数学做题与解题中，建构知识体系，提炼数学思想，渗透数学文化，提升数学核心素养.只有明素养导向，方可促深度学习！