基于数学本质的一道平面向量典型试题的研究与拓展*

(镇海中学,浙江 宁波 315200)

平面向量是高考考查的重点知识，近3年的《浙江省高考考试说明(数学)》对它的考试要求都用了“理解”“掌握”“会用”等字眼.从教学层面来看，向量是沟通代数、几何与三角函数的一种有力工具.但遗憾的是，从学生层面来看，向量试题往往成为他们解题路上的一道坎，他们或许知道从何开始，却不知在何处结束.

在2018学年第二学期浙江省名校协作体联考中，就有这么一道向量试题让学生望而却步.笔者抓住机会，全方位、多角度剖析这道试题，并对其进行了研究与拓展.正如波利亚所言：“一个有责任心的教师与其穷于应付繁琐的教学内容和大量的题目，还不如选择一个有意义但又不太复杂的题目去帮助学生深入挖掘题目的各个侧面，在指导学生解题的过程中，提高他们的才智与推理能力.”[1]

1 试题呈现及分析

例1若平面向量a,b,e,满足|a|=2，|b|=3，|e|=1且a·b-e·(a+b)+1=0，则|a-b|的最小值是

( )

本题主要考查平面向量数量积的运算，同时考查学生运用等价转化、数形结合等思想方法解决问题的能力及逻辑推理、直观想象、数学运算等数学核心素养.本题知识综合性强，能力要求高，但没有脱离对主干内容的研究.解决的关键是如何将模的最值问题转化为函数最值问题或几何最值问题[2].

2 解法探究

解决平面向量数量积问题有3个视角：代数运算、几何直观和坐标表示，不同的视角缘于我们对概念的不同认识.

2.1 代数运算:a·b=|a|·|b|cos θ

解法1设a与b的夹角为θ，e与a+b的夹角为β，从而

a·b=6cosθ,

于是a·b-e·(a+b)+1=

解得

因为|cosβ|≤1，所以

解得

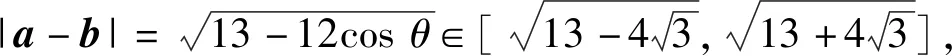
评注遇到向量的数量积问题，首先应该考虑运用数量积的定义(a·b=|a|·|b|cosθ)，将向量运算转化成数量运算，从而将问题转化为双变元的三角函数最值问题，用三角函数的有界性构造不等式，恰到好处.

2.2 几何直观：a·b=0⟺a⊥b

解法2因为a·b-e·(a+b)+1=(a-e)·(b-e)=0，所以

(a-e)⊥(b-e).

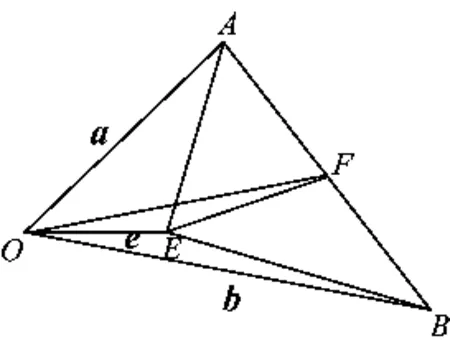
图1

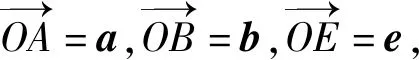
且满足|OF|≤|OE|+|EF|，即

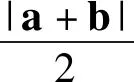
解得

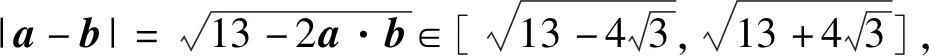
评注观察题干中向量式子的结构特征，将其转化为(a-e)·(b-e)=0后，本题的几何特征显现.将垂直转化为圆的问题后，就不难发现△OEF中三边存在的不等关系.

2.3 坐标表示：a·b=x1x2+y1y2

解法3考虑到平面向量a,b,e位置的相对性，不妨设a=(2,0),b=(3cosθ,3sinθ),e=(cosβ,sinβ),则

a·b-e·(a+b)+1=6cosθ-cosβ·(2+

3cosθ)-sinβ·3sinθ+1=0,

整理成关于β的函数，得

(2+3cosθ)cosβ+3sinθsinβ=6cosθ+1，

解得

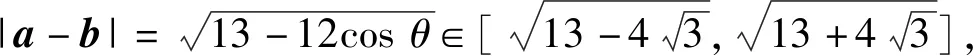
评注建系和设坐标已经成为不少学生解决向量问题的“救命稻草”.我们可以通过坐标运算将向量问题直接“翻译”成代数问题.但是，在解决与之相关的代数问题时，还需要学生有较强的处理多变量代数运算的能力.

3 纵深挖掘

3.1 代数运算重观

本题的关键是要“消除”e对a,b的“影响”，即如何处理e·(a+b)这个运算.事实上，在处理数量积最值问题时常常会用到不等式|m·n|≤|m|·|n|，而这个不等式的好处是将数量积定义中3个变量间的关系转化成两个模之间的关系，从而消除了角度的影响.这也是解法1的本质.

当然，如果从结构上重新认识等式

a·b-e·(a+b)+1=0，

或许会有新的发现.我们知道

因为

||a+b|-|e||≤|a+b-e|≤|a+b|+|e|,

所以

又

|a+b|2+|a-b|2=2(|a|2+|b|2)=26，

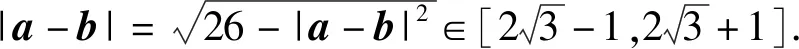
在上述解答过程中，我们用到了处理向量最值问题时用到的另一个重要不等式(向量三角不等式):||m|-|n||≤|m+n|≤|m|+|n|.

3.2 几何图形重观

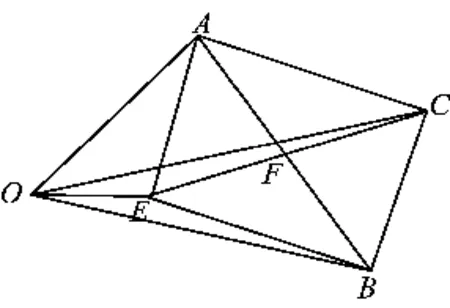
图2

重观图1，若将△AEB补成如图2所示的矩形AEBC，则本题的本质应该是矩形中的一个重要性质：

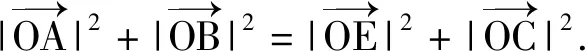
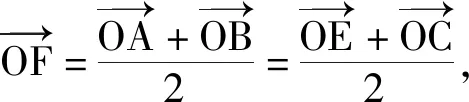
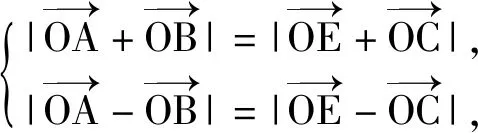
两式平方相加，得

从而

在△OEC中，

又AB=EC，故

这道题的原型就是2013年重庆市数学高考理科试题第10题：

( )

3.3 拓展延伸

事实上，当我们把向量条件几何化之后，就变成了解三角形问题：

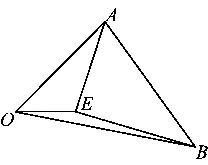
图3

例3如图3，在△AOB中，已知OA=2，OB=3，OE=1,AE⊥BE,求AB的最小值.

解此时可设∠AEO=α，∠BEO=β，AE=x，BE=y,则

即cos2α+cos2β=1(当图形变成如图4～6的情况时，同样有cos2α+cos2β=1).

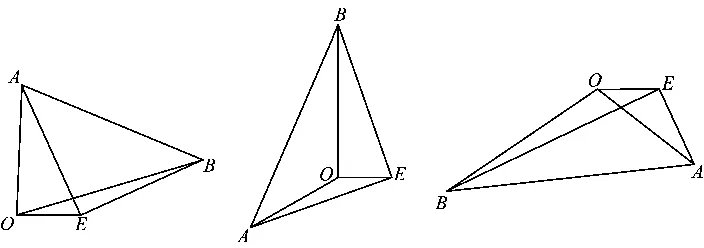
图4 图5 图6

在△AOE,△BOE中，由余弦定理可得

从而

即

展开得

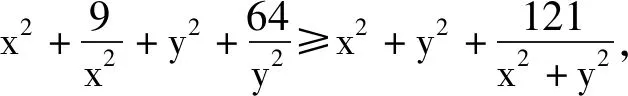
解得

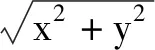
4 反思感悟

平面向量是高中数学的重要知识，也是沟通代数与几何的一种有力的工具.解决平面向量问题往往有3个视角：代数运算、几何直观和坐标表示.方法很明确，但是为什么学生还是无法越过向量的坎呢？我们应该多从课本中原有的知识点出发，以题目为载体，加强学生的知识运用能力.

比如，本文例题中蕴含的平面向量中的两个重要不等式||m|-|n||≤|m+n|≤|m|+|n|和|m·n|≤|m|·|n|是课本中已有的知识点，但是不少学生仅仅只是了解，更别谈应用.这时，一方面我们教师应该敏锐地观察到这一点，通过典型例题，加强这个知识点的运用；另一方面，在学生陷入题海战术时，要做好“引路人”，在引导学生“如何思”“如何想”的同时，帮助学生挖掘问题的本质，抓住问题的生长点，最终解决问题.