解读分段函数问题

■李志勤

分段函数是高中数学常见的函数，分段函数一直是高考考查的热点。在学习分段函数时，熟悉分段函数的概念，掌握基本初等函数的图像与性质，领会函数的基本思想方法，才能完整地解决分段函数的相关问题。求解分段函数问题的关键是“分段归类”。下面结合具体例题，总结分段函数的常考题型与解题方法。

一、分段函数的单调性问题

例1若分段函数f（x）=在R上是增函数，则实数a的取值范围为（ ）。

A.（-∞，1] B.（0，2）

C.（0，1] D.[1，2）

解：利用分段函数在每一段上都是单调递增解出a的范围。

因为函数f（x）在R上是增函数，所以解得0＜a≤1。故实数a的取值范围为（0，1]。应选C。

评析：分段函数f（x）=在 上单调递增，则函数Rf（x）满足：f1（x）在（-∞，a]上单调递增，f2（x）在（a，+∞）上单调递增，且f1（a）≤f2（a）。

二、分段函数的求值问题

例2设分段函数f（x）=

解：把所求自变量转化到x＜1的范围内，再代入分段函数即可求值。因为函数所以f（log10）=2

评析：解决分段函数求值问题，要明确自变量所属的区间。解答本题的关键是借助函数的周期性将自变量的值转化到分段函数的定义域上求解。

三、分段函数的求参数问题

例3已知分段函数f（x）=其中0＜m＜1，若存在实数a，使得关于x的方程f（x）=a恰有三个不同的实根，则m的取值范围是（ ）。

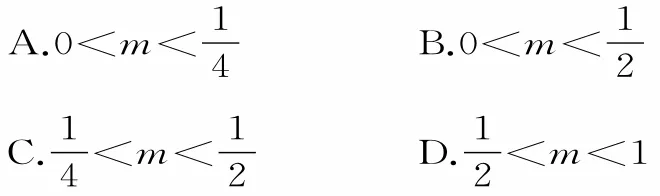
解：作出函数f（x）的图像，得到关于m的对数不等式求解即可。当0＜m＜1时，函数的图像如图1所示（简图）。

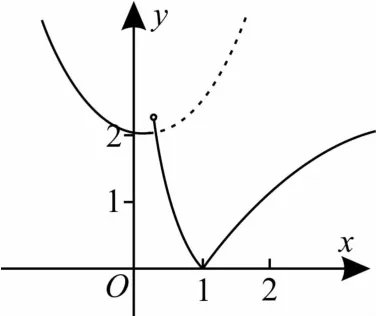
图1

当x≤m时，f（x）=x2-2m x+m2+2=（x-m）2+2≥2，要使关于x的方程f（x）=a有三个不同的实根，需满足又0＜m＜1，解得应选A。

评析：本题考查方程的根的存在性及根的个数判断问题。解答本题的难点是分析得到