函数模型及其应用学习导航
■聂森林
函数模型及其应用是高中数学的重要内容,也是高考的常考点,同学们一定要理解和掌握几种常见的函数模型,学会应用函数的模型解决实际问题。
一、要点梳理
1.几类函数模型及其增长差异
2.解函数应用问题的几个步骤
(1)审题:弄清题意,分清条件和结论,理顺数量关系,初步选择数学模型。(2)建模:将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型。(3)求模:求解数学模型,得出数学结论。(4)还原:将数学问题还原为实际问题的意义。
二、特别提示
求解函数应用问题时,一要弄清问题的实际背景,注意隐含条件;二要将文字语言恰当准确地翻译为数学语言,用数学表达式加以表示;三要弄清给出什么条件,解决什么问题,通过何种数学模型加以解决;四要严格按照各种数学模型的要求进行推理运算,并对运算结果作出实际解释。
三、例题精析
1.森林砍伐问题
例1一片森林原来面积为a,计划每年砍伐一些树木,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的,已知到今年为止,森林剩余面积为原来的
(1)求每年砍伐面积的百分比。
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
解:(1)设每年砍伐面积的百分比为x(0<x<1),则,即(1-x)10,解得故每年砍伐面积的百分比为
(2)设经过m年剩余面积为原来的则,可得解得m=5。故到今年为止,该森林已砍伐了5年。
(3)设从今年开始,以后砍伐了n年,则n年后剩余面积为,即,即,解得n≤15。故今后最多还能砍伐15年。
评析:在实际问题中,人口增长,银行利率,细胞分裂等增长问题,都可以利用指数函数模型来表示。
2.蔬菜上的农药清洗问题
例2用水清洗蔬菜上的残留农药,显然用水越多洗掉的农药量越多,但总还有农药残留在蔬菜上。设用x单位量的水清洗一次以后,蔬菜上残留的农药与本次清洗前残留的农药量之比为函数f(x),可设f(x)=现有a单位量的水,可以一次清洗,也可以把水平均分成2份后清洗两次,试问哪种方案清洗后蔬菜上残留的农药量比较少。请说明理由。
解:a单位量的水,清洗一次,残留的农药量为其中f(0)=1表示没有用水清洗时,蔬菜上的农药量保持原样,设为1。
把a单位量的水均分成2份后清洗两次,残留的农药量为
评析:本题属于一个模型化了的问题,就是说从题意出发已经假定了一个数学模型,即,这种假定的数学模型是解答本例的关键。
3.拟合函数问题
例3某个体经营者把开始六个月试销A,B两种商品的逐月投资与所获纯利润列成表1。
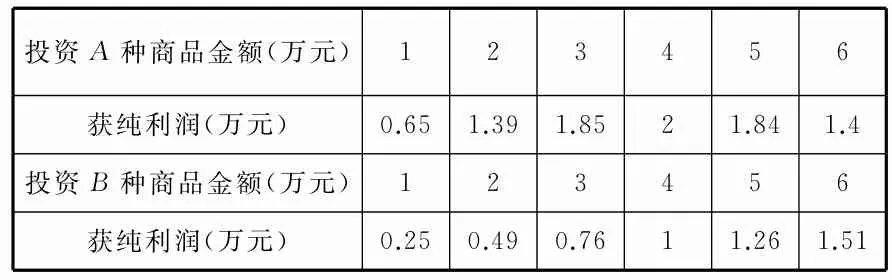
表1
该经营者准备下月投入12万元经营这两种产品,但不知投入A,B两种商品各多少万元才合算。
请你帮助制定一个资金投入方案,使得该经营者能获得最大利润,并按照你的方案求出该经营者下月可获得的最大纯利润。
解:以投资额为横坐标,纯利润为纵坐标,在平面直角坐标系中分别画出A,B两种商品的散点图(图略)。观察散点图可以看出,A种商品所获纯利润y与投资额x之间的变化规律可以用二次函数模型进行模拟。取(4,2)为最高点,则y=a(x-4)2+2,把点(1,0.65)代入此方程解得a≈-0.15,所以y=-0.15(x-4)2+2。B种商品所获纯利润y与投资额x之间的变化规律可以用一次函数模型进行模拟。设y=k x+b,取点(1,0.25)和(4,1),代入此方程解得k=0.25,{b=0, 所以y=0.25x。
故前六个月所获纯利润y关于月投资A种商品的金额x的函数关系式是y=-0.15(x-4)2+2;前六个月所获纯利润y关于月投资B种商品的金额x的函数关系式是y=0.25x。设下月投入A,B两种商品的资金分别为xA,xB,总利润为W,则xA+xB=12,W=yA+yB=-0.15(xA-4)2+2+0.25xB。于是可得故当元)时,W取最大值,约为4.1万元,此时xB=8.8(万元)。故该经营者下月把12万元中的3.2万元投资A种商品,8.8万元投资B种商品,可获得最大利润约为4.1万元。
评析:对于拟合函数模型问题,解题的关键是建立适当的函数关系式。

