基于极限学习机的蚜虫刺吸电位波形的分类识别∗

吴莉莉，邢玉清，林爱英，郑宝周，潘建斌，闫凤鸣

(1.河南农业大学理学院，郑州450002；2.河南农业大学植物保护学院，郑州450002)

蚜虫是一类体型很小的植食性刺吸式昆虫， 大多数是重要的农林害虫，如棉蚜、桃蚜、大豆蚜、禾谷缢管蚜等，是世界上最具破坏性的害虫类别之一；蚜虫还是植物病毒最主要的传毒介体类别之一。昆虫刺吸电位仪(Electrical Penetration Graph，EPG)作为进行昆虫取食行为、昆虫传毒机制、作物抗虫机制等方面研究的有力工具[1-2]，可以为包括蚜虫在内的刺吸式昆虫的防控方法研究及其所传播植物病毒的机理研究提供技术支撑，目前已成功应用于蚜虫、粉虱、飞虱、叶蝉、蓟马、蝽等50多种昆虫的相关研究。但EPG波形的识别和分析一直是靠人工进行，费时费力，很大程度上限制了EPG技术的应用和作用的发挥，因此迫切需要EPG波形的自动识别。

EPG技术最早应用于蚜虫取食行为的研究，现阶段国内外对蚜虫的EPG波形研究也最深入和广泛。蚜虫EPG波形典型且稳定，不同蚜虫种类的EPG波形差异很小，是进行其他类别昆虫EPG波形识别的重要参考。结合透射电镜、同位素示踪、口针切割等技术，已明确了蚜虫的7种基本波形及其生物学意义，见表1。这7种波形分别为np波(非刺探波，此时蚜虫口针未刺入植物表皮内，波形几近直线)、C波(路径波，包含A波和B波，在判读中一般将一些不能明确区分的波也归入C波)、pd波(口针穿刺波)、E1波(韧皮部分泌唾液波)、E2波(韧皮部取食波)、G波(木质部取食波)和F波(机械障碍波)[2]。

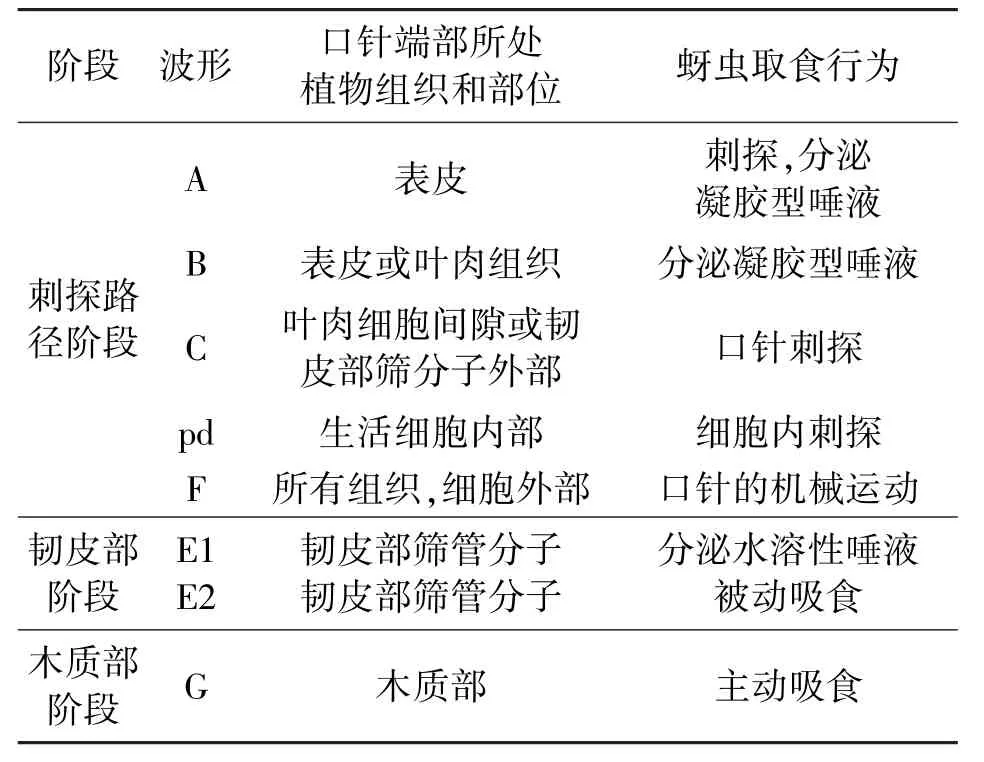
表1 蚜虫EPG波形的生物学意义

目前国内外对蚜虫EPG波形分类识别研究的报道仅有两例。2015年Adasme-Carreo等[3]研发了一个EPG波形分析系统，即A2EPG(Assisted Analysis of Electrical Penetration Graph)，该系统能识别np、C、pd、G和 E1波并统计各波段的持续时间。然而A2EPG对EPG波形的识别率并不高，对np波和pd波的识别效果很好，对E2波完全不能识别，对其他波形(如G波、E1波)会经常错判为C波，因此在使用该系统时需要用户重新审查结果。

A2EPG识别率不高的主要原因在于特征提取和识别算法过于简单，仅提取了时域波形中的极值和斜率等特征，对于时频和非线性特征均未考虑；这种特征提取方法虽然能在一定程度上减少运算量，也能部分代表波形的主要特征，但是波形中的很多细节特征都被忽略了。另外在波形识别算法上面，A2EPG使用的是二元分类法，该方法相对于机器学习中的人工神经网络等分类器算法在自学习、非线性数据处理等方面能力较弱。

2018年吴莉莉等[4]以桃蚜的EPG波形为研究对象，对 np、C、pd、E1、E2、G 和 F 波的特征提取和分类识别进行了研究，提出了融合分形维数和希尔伯特-黄变换(hilbert-huang transform，HHT)的特征提取方法，构建了基于决策树的分类器，通过对4组不同样本进行测试，得到了91.43%的平均识别率。与人工相比，机器识别的耗时仅为人工识别的1/46，极大地提高了工作效率。

笔者的前期研究仅对非线性特征提取和决策树分类器进行了初步探讨，其他特征如时频特征等均未考虑，机器学习中的其他分类算法对EPG波形分类是否会得到更高的识别率也未进行探讨，因此本文拟采用不同的特征提取方法和分类器进行EPG波形分类识别的进一步研究，期望找到最佳的特征向量和分类器组合来提高识别性能。

1 极限学习机

极限学习机(Extreme Learning Machine，ELM)是由Huang等[5]针对传统神经网络训练速度慢、易陷入局部极小值等问题提出的一种单隐含层前馈神经网络(Single-Hidden Layer Feedforward Neural Network，SLFN)，该算法中输入层与隐含层间的连接权值以及隐含层神经元阈值都是随机产生的，网络在训练过程中只需设置隐含层神经元的个数即可获得唯一的最优解，与传统的SLFN相比具有学习速度快、泛化性能好等优点，因此广泛应用于回归拟合和分类识别中[6-10]。

ELM的网络结构如图1所示，由输入层、隐含层和输出层组成，输入层与隐含层、隐含层与输出层间的神经元采用全连接。

设输入层有n个神经元，对应n个输入变量；隐含层有l个神经元；输出层有m个神经元，对应m个输出变量。输入层与隐含层间的连接权值矩阵为w，隐含层与输出层的连接权值矩阵为λ，隐含层神经元的阈值矩阵为b，则

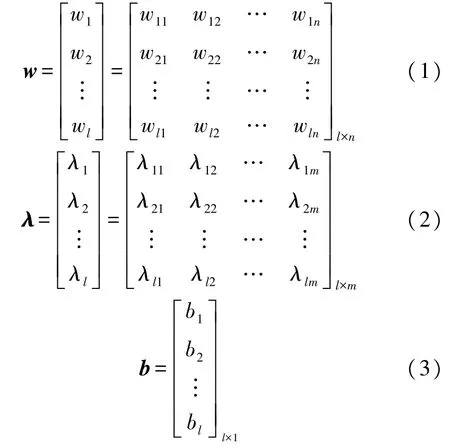
设隐含层神经元的激活函数为g(x)，则网络的输出Y为

式中:H为隐含层输出矩阵，N为输出样本个数。

根据Huang提出的两个定理可知:①若隐含层神经元个数与训练样本个数相同，对于任意的w和b，ELM都可以零误差地逼近训练样本；②当训练样本个数较大时，为了减小计算量，隐含层神经元个数通常取得小于训练样本个数，ELM的训练误差可以逼近任意一个ε＞0。

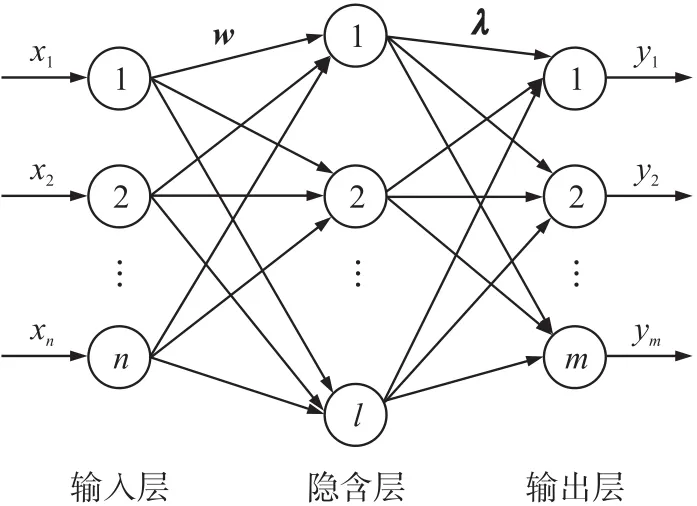
图1 ELM的网络结构图

因此当激活函数g(x)无限可微时，ELM无需调整全部参数，w和b在训练前可以随机选择，且在训练过程中保持不变。而隐含层与输出层的连接权值λ可以通过式(6)的最小二乘解获得。

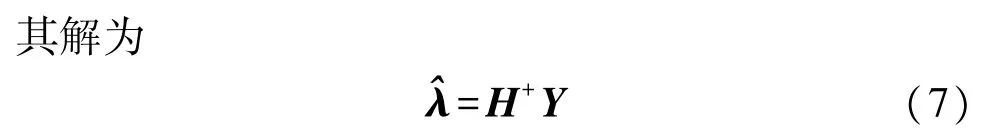
式中:H＋为隐含层输出矩阵H的Moore-Penrose广义逆。

在ELM中一些常用的激活函数[7]有如下几种:

①高斯函数

④多元二次函数

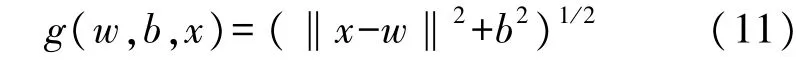
ELM算法的实现主要有以下三个步骤:①随机设定输入层与隐含层的连接权值w以及隐含层神经元阈值b，确定隐含层神经元个数；②选取隐含层激活函数，计算隐含层输出矩阵H；③计算隐含层与输出层的连接权值＾λ:＾λ＝H＋Y。

2 EPG波形分类实验

EPG波形主要由EPG仪器采集获得，经过预处理之后进行特征提取和分类识别。EPG波形的采集和预处理方法详见文献[4，11]，这里不再赘述。

2.1 小波能量特征的提取

EPG信号是一种幅度和频率随时间变化的非平稳信号。小波变换作为一种非平稳信号分析方法，可以将信号分解成各种不同频率成分或不同尺度成分，通过伸缩、平移聚焦到信号的任一细节加以分析，具有优良的时频特性[12-13]。小波系数可以表达信号在时频两域的能量分布，因此实验中拟提取小波系数能量作为EPG波形的时频特征。

EPG波形的小波能量特征提取方法如下:

①对EPG信号进行j层小波分解，得到各层的小波分解系数 Cj，k；

②计算各分解层的平均能量分布:将某层的分解系数先平方再求和，即:

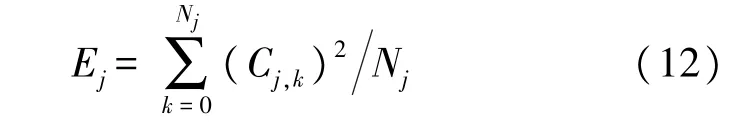
式中:为 j为分解层数，Nj为第 j层小波系数的长度；

③筛选得到的各层平均能量，组建特征向量。

由于EPG信号的采样频率为100 Hz，EPG各种波形的频率主要集中在2 Hz～20 Hz，因此实验中对EPG信号进行6层sym4小波分解，提取2～5层的高频、低频系数的平均能量，如图2所示。图2中给出了每种波形各100个样本的小波能量平均值，A2～A5代表第2～5层小波分解的低频系数，D2～D5代表第2～5层小波分解的高频系数，显然EPG各种波形在在低频能量部分差异较明显，高频能量部分不易区分，因此选用低频能量融合其他特征组建特征向量。

图3所示为EPG的7种波形各100个样本第2～5层低频小波系数平均能量的特征值分布。从图中可以看出，G波的第2～4层特征值比较集中，数值稳定，与其他特征值交叉较少，易于区分；E1波第2～5层的特征值比较分散，且数值差异较大，这对于后续的分类是不利的，说明小波系数的平均能量不能很好的表征E1波，还需要融合其他特征。

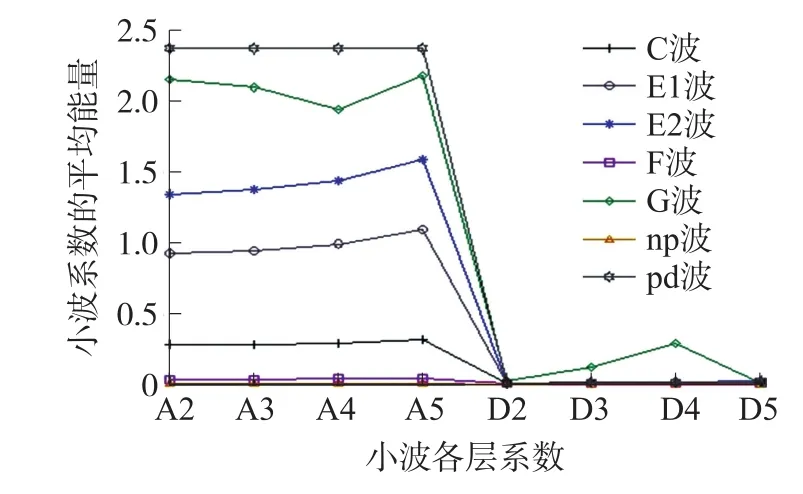
图2 第2～5层小波系数的平均能量对比图

图3 EPG波形的小波系数平均能量特征值分布

2.2 特征向量的组建

文献4中采用的是分形维数和HHT的特征组成特征向量，在利用决策树进行分类时发现，第2层的加权频率特征几乎没有用到，所以实验中将其替换成小波能量特征。由于不知道哪几种特征组合对分类更有利，只有根据分类的实验结果进行选择[14]。

实验中将采用5种不同的特征向量组合来进行对比选择。第1组特征向量 S1由分形盒维数、Hurst指数、第2～5层的低频小波能量组成，共6个特征；第2组特征向量S2由HHT前2层谱质心、第2～5层的低频小波能量组成，共6个特征；第3组特征向量S3由分形盒维数、Hurst指数、HHT前2层谱质心、第2～5层的低频小波能量组成，共8个特征；第4组特征向量S4由分形盒维数、Hurst指数、HHT前2层谱质心、第2～3层的低频小波能量组成，共6个特征；第5组特征向量S5由分形盒维数、Hurst指数、HHT前2层谱质心、第4～5层的低频小波能量组成，共6个特征。

为了与前期实验结果方便对比，采用与文献4完全相同的训练样本、测试样本和分类器，各种不同特征组合的识别结果如表1所示。从表1中可以看出，采用S4特征向量组合得到的平均识别率最高，为91.61%，S5特征向量组合得到的平均识别率与文献4相同，为91.43%，因此本文采用S4作为特征向量，进入ELM分类识别。

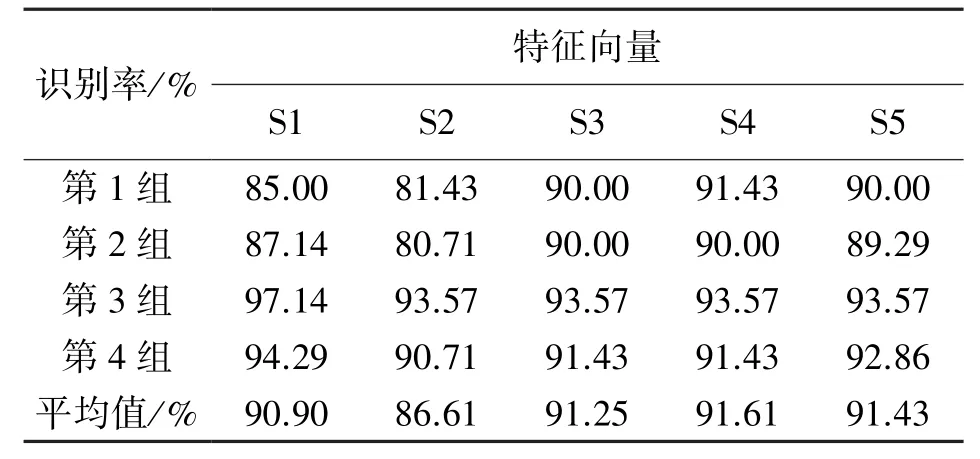
表1 不同特征向量的分类识别率对比

2.3 基于ELM的分类识别

实验中将对EPG信号中的C波、E1波、E2波、F波、G波、np波和pd波共7种波形进行分类识别，S4作为特征向量进入ELM分类器，共进行4组测试(与文献4中的4组样本完全相同)。ELM作分类器时，初始连接权值和隐含层阈值随机设置，为了确保每次分类结果稳定，将其固定，每次运算都使用这个随机值。隐含层经元个数不同，对分类效果影响很大，图4给出了当神经元个数取值从20～400时，4组测试样本的分类识别率，可以看出神经元个数并非越多越好，而且随着神经元个数的增加，识别率呈下降趋势。

图4 隐含层神经元个数对ELM分类性能的影响

ELM的隐含层神经元个数究竟取多少可以获得最好的分类性能，目前尚缺乏理论指导，为了获得最佳的识别率，实验中对ELM算法进行了改进，采用增量型算法自适应地选择隐含层神经元个数[15-16]。通过逐个增加隐含层神经元个数来确定最佳的网络结构，在每次迭代过程中添加新的神经元后，更新已有隐含层神经元的输出权值和期望余差，直至余差接近期望值，便可求得符合要求的最小隐含层神经元个数及各隐含层神经元参数。

2.4 实验结果及分析

实验中将相同的样本分别进入决策树和概率神经网络(Probabilistic Neural Network，PNN)分类器中，从识别率和耗时两方面进行对比，实验结果如表2所示。从表2中的4组数据的平均分类结果来看，采用PNN的分类识别率最低，为90.72%，ELM的识别率最高，平均识别率为93.57%；决策树分类器的耗时最长，ELM的耗时最短，平均耗时14.95s；综合识别率和耗时两方面来看，采用ELM分类器获得了较好的分类性能。从单组测试数据来看，第1组和2组采用决策树的识别率较高，第3组和第4组采用ELM的识别率较高。

表2 决策树、ELM和PNN的分类性能对比

造成分类结果差异较大的原因主要有以下几个方面:①EPG信号属于生物电信号，受外界干扰和受试昆虫的影响较大，即使是同种波形其幅值、频率间也会有差异，尤其是对于较复杂的C波，前1 h与后1 h的波形走向都会不同，这就导致了提取的特征值分散，识别时容易误判；②实验中采用的分类器算法都属于有导师学习，如果训练样本的选取不够全面，当训练样本与测试样本差异较大时，就会出现识别率较低的情况。

3 结束语

在利用EPG技术进行昆虫与植物相关研究时，一直以来都是靠人工识别波形，机器识别在EPG波形方面的应用研究相对于心电、脑电等生物电信号要缓慢得多。

本文对蚜虫EPG波形的特征提取和分类识别方法进行了研究，组建了融合小波能量、分形维数和HHT的特征向量，构建了基于ELM的分类器，得到了93.57%的平均识别率。为了说明本文的特征提取和分类识别方法更有效，实验中对比了不同特征向量和不同分类器的识别性能。实验结果说明在决策树分类器下采用分形盒维数、Hurst指数、HHT前2层谱质心、第2～3层的低频小波能量组成的6维特征向量识别效果最好，平均识别率可达91.61%，相比于前期研究(文献4的平均识别率为91.43%)提高了0.18%；当采用ELM分类器时，四组样本的平均识别率提高了2.14%；与决策树和概率神经网络相比，ELM分类器不仅识别率高且耗时短，具有较好的分类性能。本文的研究将为开发EPG波形自动识别分析系统奠定理论基础，促进机器学习在EPG领域的应用。