考虑温度影响的砷化镓光子晶体压力传感器的设计与研究

夏 雨，陈德媛，陈 兵，张 岩，李梦凡

(南京邮电大学电子与光学工程学院，微电子学院，南京210023)

光子晶体是一种人工微结构，最初光子晶体这一概念是由Yablonovitch E和John S在1987年分别独立提出的[1-3]。它由不同折射率的介质按照周期性规律排列而成，按维度可分为一维、二维和三维结构[4]，而由于制备和光学特性等多方面因素，受到广泛研究和应用的是二维光子晶体。光子禁带(光子带隙)和光子局域是光子晶体的根本的、且很重要的特性[5]。利用光子晶体的特性可以实现对光子的引导和控制。至今，光子晶体被用于在功能器件[6-7]、光子晶体光纤[8]、光子晶体传感器如温度传感器[9]、生物传感器[10-11]、压力传感器[12-13]等等多个领域的研究和器件制备。其中光子晶体压力传感器利用光子晶体的压弹特性实现对压力的探测，具有较高的灵敏度而备受关注。Shanthi等人设计了一种基于二维光子晶体的压力传感器，其灵敏度为2 nm/GPa，动态范围可以达到7 GPa[14]。Olyaee S等人利用光子晶体波导结构和纳米谐振腔结构设计了具有较高灵敏度的光子晶体压力传感器，其使用Si作为衬底，与目前的集成电路生产工艺能够较好地兼容，且灵敏度达到了8 nm/GPa[15]。南京邮电大学陶尚彬基于GaAs衬底设计出了具有较高品质因子和灵敏度的孔型三角格子压力传感器，灵敏度达到了13.9 nm/GPa，该传感器性能更好，结构更优，易于制造[16]。上述几种光子晶体压力传感器的设计均是考虑器件在恒温情况下工作，且多是从提高灵敏度，品质因子方面研究压力传感器。而其他压力传感器多是使用对温度敏感的材料来研究，显而易见温度敏感材料必须考虑温度的影响，仅此研究方向不存在研究独特性。本文结合实际环境考虑，通常情况下，器件实际工作的环境不能保证恒温状态，如环境温度变化较大时，热膨胀效应和热光效应会导致材料的折射率变化，从而引起器件的探测偏离实际情况，导致零漂和灵敏度偏差。因此，本文提出了一种基于砷化镓的二维光子晶体压力传感器，设计双通道探测结构，分析和研究温度对压力测量的影响，提高器件的探测准确性和灵敏度。

本文设计的二维光子晶体压力传感器采用具有较强压弹特性的砷化镓材料，设计双通道光子晶体滤波器[17-18]，分别用于探测温度和压力。滤波器均是利用腔和波导耦合而实现的窄带带通滤波器。压弹特性使得砷化镓材料的折射率在压力下发生变化，相应的滤波器滤波模式波长产生线性变化，从而实现压力探测。砷化镓材料也有一定的热光效应，在温度变化情况下，折射率也会产生变化，从而导致对应的温度滤波器的滤波模式波长产生线性变化，实现温度探测。本文以25℃(室温)、0 GPa压力为参考，仿真出所处温度及压力下的滤波模式波长，可以根据公式计算当前环境温度，继而得出相应温度下的压力值，研究温度对压力测量的影响。本文采用有限元法进行仿真设计和分析，研究了恒温情况下压力探测灵敏度、恒压情况下温度的探测以及温度和压力同时变化的探测结果，分析了滤波器的品质因子、滤波模式波长、透射率等的变化情况等。

1 理论计算

在压力作用下，根据材料的压弹特性，滤波器的滤波模式波长与压力之间的线性关系测量压力的变化。而根据热光效应，在温度变化的情况下，滤波器的滤波模式波长与温度之间呈线性的关系可用于测量温度变化。

折射率与压力的表示关系如式(1)[19-21]:

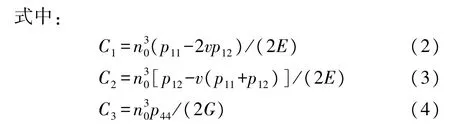
式中:p11、p12、p44，E、G，v，nij，σij分别代表光弹性系数，杨氏模量、剪切模量，泊松比，ij方向上的折射率和ij方向受到的压力(ij代表自然数)。

假设我们是纵向施加压力的，即沿柱的方向(基于二维则是向XY面的方向)且面内各个方向所受压力相同，则

式中:n0为零压力时的介质折射率，σ为施加的压力。

砷化镓材料的光弹性系数C1(10-12/Pa)为-18.39，C2(10-12/Pa)为-10.63，光弹特性较显著，适合用于制备压力探测器件，因此本文选择砷化镓材料作为光子晶体衬底材料，其折射率是3.43，p11＝-0.165，p12＝-0.140[22]。

砷化镓材料也具有一定的热光效应和热膨胀效应，在温度变化情况下，由于介质材料的热光效应和热膨胀效应，折射率会产生变化，从而滤波模式波长产生相应的线性变化[23]。折射率计算公式[24]如下:

式中:n0是25℃(室温)下的材料折射率，n是温度变化后的材料折射率，T0为室温，T为变化后的温度。式(8)中砷化镓的线性热光系数εT＝149×10-6μm/℃。

2 二维双通道光子晶体压力传感器的结构设计和性能分析

2.1 结构设计

该二维光子晶体压力传感器包含双通道滤波器，分别用于压力探测和温度探测。如图1，左边部分是探测压力的滤波器，右边部分是探测温度的滤波器。光子晶体结构为31×21砷化镓介质柱阵列，晶格常数a为580 nm，介质柱半径r为120 nm，背景材料为空气。结构中通过去除介质柱的方式设计了三分支波导如图所示，输入波导w1，输出波导w2和w3。在两个输出波导上分别设计了两个具有一定品质因子的腔2和腔3，分别用于实现压力测量中的滤波和温度测量中的滤波功能。输入波导w1到输出w2之间呈90°转角，并设计对称分布但非均匀大小的7个介质柱形成腔结构如图所示，其半径分别为:中心半径为2.2r的介质柱，中心柱两侧分别配置半径为r的一个介质柱，最外侧是各两个半径为0.606r的介质柱，材料仍然为砷化镓。波导w3则以礼帽形结构呈现，左侧通过礼帽边与输入波导w1耦合，右侧礼帽斜边上额外配置两个介质柱，位置为完美结构的晶格格点位置如图1所示，形成腔3。

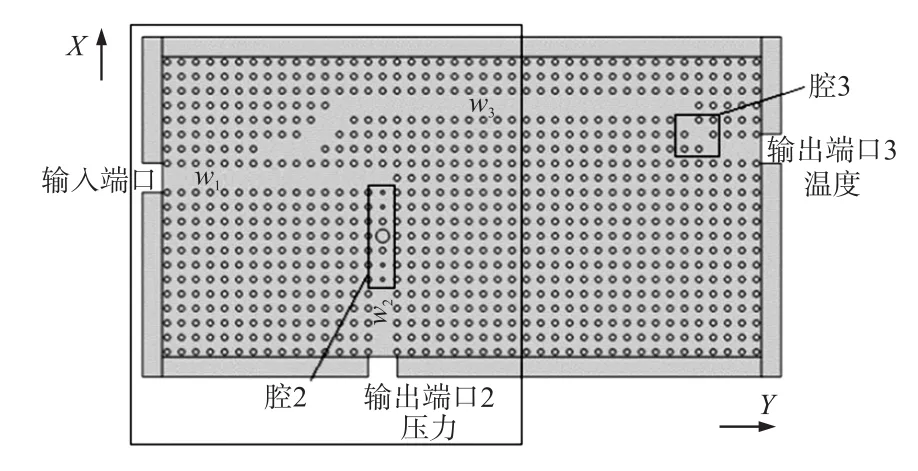
图1 光子晶体压力-温度双输出通道传感器结构

该结构左侧为压力探测部分，工作的时候，压力只施加在左侧部分，由2号端口输出来计算压力。外加压力不影响右侧温度部分的探测。在一定温度下，由于温度的影响，必定导致压力探测的数据中包含了温度的影响，因此2号端口输出实际上是压力温度共同作用的结果，需要结合3号端口的输出结果，去除温度的影响，从而得到高灵敏度的压力探测。本文采用有限元法，通过数值分析，结合数学拟合消除温度的响应，得到更接近真实情况的压力值。

2.2 性能分析

根据上述滤波器结构，腔2与腔3分别与波导W2和W3耦合[25]实现了窄带带通滤波功能，并且根据腔2和腔3结构的不同仿真出了室温下不同耦合频率的模式场分布图，分别如图2和图3所示，腔2、腔3分别局域了不同频率(波长)的光。此时，两个滤波器的腔模式对应的滤波波长分别是λ1＝1 471 nm，λ2＝1 529.9 nm。而在-25～45℃动态范围内温度发生改变以后(温度变化步长是10℃)，2号端口和3号端口滤波波长产生线性红移，分别监测出2号端口和3号端口输出透射谱，如图4和图5。根据对应数据分别计算出两个端口的温度灵敏度系数:2号端口温度灵敏度系数是k2＝0.2/10＝0.02 nm/℃，3号端口温度灵敏度系数是k3＝0.07/10＝0.007 nm/℃。并且在图6中给出了此时3号端口滤波波长随温度线性变化曲线。

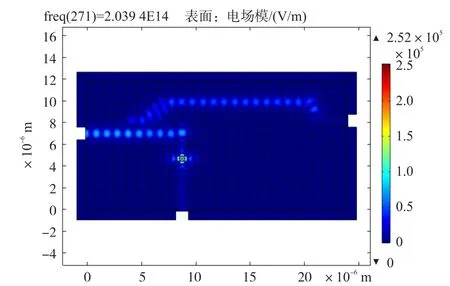
图2 腔2室温下频率耦合的模式场图

图3 腔3室温下频率耦合的模式场图

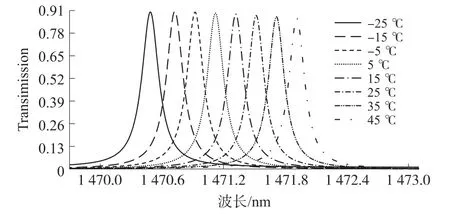
图4 -25℃～45℃下2号端口的透射谱

图5 -25℃～5℃下3号端口的透射谱

图6 -25℃～45℃下2号端口滤波波长线性变化

为研究温度对压力测量的影响，双通道滤波器中温度探测同时作为压力测量的温度参考，并且利用数学拟合消除该温度的影响。根据上面计算出的温度灵敏度系数及推算出的2号端口滤波波长变化量Δλ2和3号端口受温度作用下的滤波波长变化量ΔλT3，压力端口最终滤波波长变化量Δλpresssure可以通过式(9)[14]计算得出，

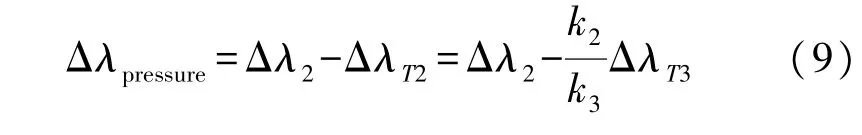
图7中显示了在0～2 GPa的动态范围内，三种不同测量温度下，2号端口滤波波长随温度变化曲线，分别是5℃、25℃和45℃时滤波波长随温度变化情况:恒压时温度增加，滤波波长的红移量增大；恒温时外加压力增大，滤波波长的红移量同样会增大。而且可以得出温度响应对压力测量产生了影响，而影响是否大到不可忽略我们接下来进一步验证。根据这一系列仿真数据计算出压力灵敏度和品质因子，式(10)中得出灵敏度约为15.9 nm/GPa。

图7 5℃、25℃和45℃时2号端口滤波波长线性变化

器件所处实际环境温度可能并不稳定，而图7中也显示了温度对压力测量的影响，并且根据图4分析得出极端温度与室温情况比较时滤波波长变化:图8是-25℃与25℃温度情况下的比较，滤波波长变化是1.028 nm；图9是25℃与45℃温度情况下的比较，滤波波长变化是0.397 nm，温度从-25℃提高到45℃后滤波波长变化是1.425 nm。分析最小压力值(最小分辨压力):仿真得出施加压力使与0 GPa时模式交叠处于峰值半高处的压力值是0.012 1 GPa，而波长变化是0.19 nm，见图10，而根据压力灵敏度及最小分辨压力得出最小分辨滤波波长是0.2 nm。

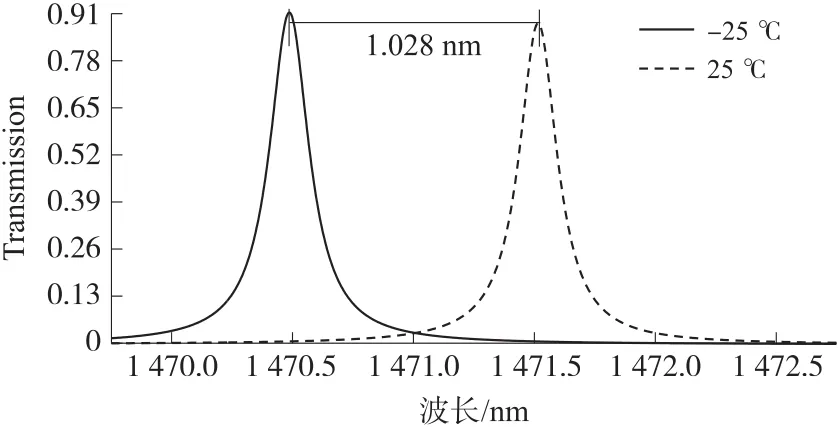
图8 -25℃与25℃比较时滤波波长变化

对比图8～图10三幅曲线图可更直观清晰地得出温度极端情况下滤波波长变化量和最小分辨滤波波长之间鲜明的差距:图10与图8和图9分别比较可以得出滤波波长变化的差距，而与图8比较得出滤波波长变化差距极大，并且两个极端温度之间滤波波长变化更大，可知温度响应对压力测量的干扰不可忽略。

图9 25℃与45℃比较时滤波波长变化

图10 零压力与最低测量压力的模式于峰值半高处交叠

下面需要用数学拟合去除温度响应，即根据式(9)计算2号端口滤波波长变化量。图11得出温度在-25℃～45℃范围内和压力在0～2 GPa范围内变化的滤波波长变化曲线。黑色方块曲线是滤波波长随压力变化的曲线；红色圆块曲线是含有温度响应的滤波波长随压力变化的曲线。由引言介绍可知，一定温度引起的热效应使材料的折射率产生变化，当传感器探测压力的时候该变化会对压力探测产生干扰，通过数学拟合消除温度响应得到图中蓝色三角曲线，据此测得的压力值较真实。

图11 压力-温度和压力单独变化滤波波长变化曲线

下面是通过设置温度-压力点，以表格形式直观地反映传感器压力灵敏度，见表1。

表1 不同温度-压力点下的滤波波长变化情况

3 结论

本文研究了温度对压力测量的干扰，以25℃(室温)、零压力的滤波模式波长作为参考。在施加一定压力的情况下，将本文所设的最低温度和最高温度下的探测结果与室温下测量结果进行比较分析滤波波长变化情况，再与通过压力灵敏度及最小分辨压力得出的最小分辨滤波波长比较，得出环境中产生较恶劣温差时温度对压力测量有不可忽略的干扰，进而利用数学拟合消除压力作用时环境温度产生的干扰，计算得出较真实压力值。在-25℃～45℃、0～2 GPa的动态范围内，未消除温度响应前压力传感器灵敏度约为16.6 nm/GPa，消除温度响应后的压力传感器灵敏度约为15.9 nm/GPa，品质因子约为5 696。最后对比参考文献可知，该传感器的灵敏度已很高，响应速度非常快，可应用于环境温差较大情况下或长距离检测等。