电感变化率对涡流传感器性能影响的仿真研究∗

荣 锋，王 一，郭翠娟，2，闫淑霞

(1.天津工业大学电子与信息工程学院，天津300387；2.天津市光电检测技术与系统重点实验室，天津300387)

电涡流传感器以其非接触、便携性、易操作、频响宽、高灵敏度等优点，广泛应用于航空、医疗、自动化等众多领域。探头线圈作为核心部件，它的大小、匝数、厚度和激励频率都会直接影响传感器的灵敏度和检测范围，因此综合考虑线圈各项参数对获得检测范围大、灵敏度高的传感器十分重要[1]。

传感器线圈的直径越小，磁场变化越快，位移灵敏度越高，分辨率越高，满足更多狭小空间条件下的测距和震动；但Q值比较低，热稳定性较差[2]。因此，在保证线圈直径足够小的前提下，最大可能的提高稳定性和灵敏度是本文的主要目的。

目前国内外研究的方向主要集中在线圈参数对电感值、涡流值、磁场分布的影响[3-5]。经过仿真发现，当电感值最大时，电感变化率却不够理想。为了达到位移与电感值变化的曲线幅度最大，更精确地进行线性拟合，本文在保证电感值足够大的情况下，选择电感变化率最大时的参数为最优参数，达到提高灵敏度的目的。

目前的仿真模型都是通过COMSOL仿真软件构建恒温条件下的稳态物理模型[6-8]，而涡流传感器在工作中温度会发生变化，导致线圈电磁特性(电导率σ和磁导率μ)变化从而引起误差。不同激励频率下的温度漂移误差不同。本文在此基础上增加瞬态温度模块，通过温度的变化对不同激励频率进行仿真，得到电感变化率随温度变化最小时的激励频率为最佳频率，从而最大限度的提高传感器热稳定性和电感灵敏度。

1 理论分析

1.1 电涡流传感器工作原理

当一个线圈通以高频交流电I1时，在线圈四周会产生一个交变磁场B1。根据法拉第电磁感应定律，变磁场B1会在空间产生感应电动势，这个感应电动势在导体内部产生感应电流I2，称之为涡流。涡流同样会产生一个变化磁场B2，由楞次定律可知，这个磁场与线圈的磁场反向。涡流磁场与线圈磁场的相互作用，导致线圈的等效电感减小。同时，由于导体中的涡流本身要消耗能量，导致线圈的等效电阻增加[9]。工作原理如图1所示。

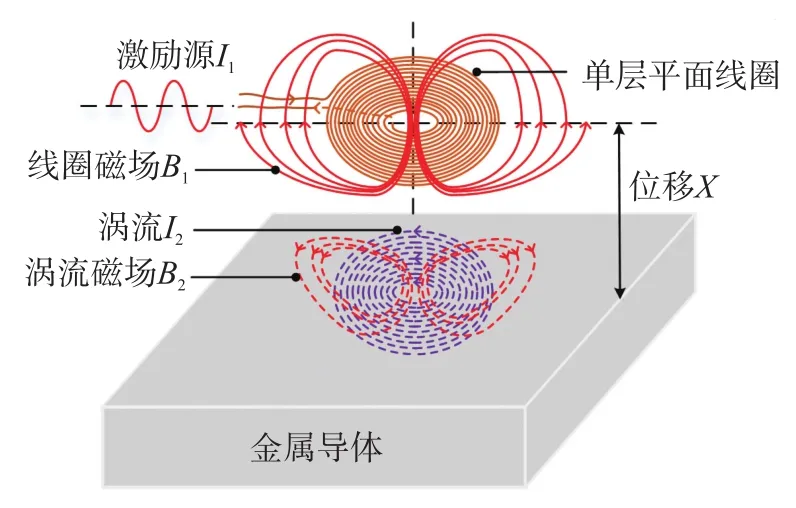
图1 电涡流位移传感器工作原理图

电涡流位移传感器正是通过改变线圈与被测导体之间的距离，从而导致线圈的等效电感和电阻发生规律性变化，从而实现对位移的检测。令被测体和线圈之间距离为X，被测体的电导率为σ，磁导率为μ，线圈的内半径R1、外半径R2、厚度h，线圈激励频率为f，则线圈的阻抗为:

1.2 线圈参数和频率的优化分析

探头线圈的电感L与线圈的参数及截面的形状有关，理论上温度变化对其影响很小，因此测量电感来反应位移变化是比较理想的。但是被测体都为金属导体，温度系数较大，所以环境温度的变化会引起涡流传感器的测量结果，而仿真发现温漂和线圈的激励频率有关。因此线圈参数和频率的优化对电涡流位移传感器来说十分重要。

1.2.1 线圈内径外径的优化分析

对于单层线圈，根据定义，电阻R的表达式为:

式中:l为导线的长度，m；A为导线的横截面积，m2；σ为电导率，S/m。表达式为:

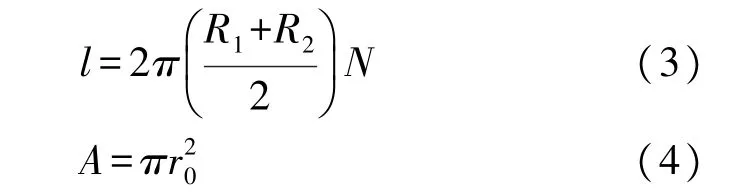
R1为内半径，m；R2为外半径，m；r0为导线横截面的半径，m。所以电阻R的表达式可化简为:

单层圆形线圈电感L可表示为[10]:

式中:K＝R1/R2，那么填充率ρ化简为:

此时Q可表示为:

其次，线圈的电感量理论上越大越好，电感越大，分辨率就越高，测量微小的变化量就越准确。电感可表示为:

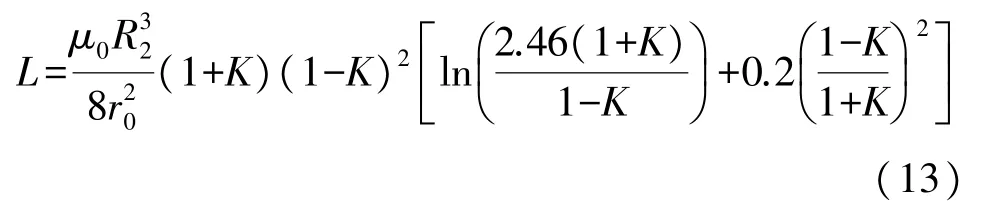
图2给出品质因子Q和电感L关于K的变化系数Q(K)和L(K)的关系，其中:

当线圈激励频率、导线尺寸和外径不变时，品质因子Q只与内外径之比K有关。当K＝0.2时Q(K)最大，可以获得最优的Q值。当K＜0.5时，Q(K)的下降率都在9%以内，均处在可接受的范围。当导线尺寸和外径不变时，L(K)随着K的增大而减小。当K＜0.3时，L(K)的下降率都在9%以内。所以，减小内径能获得更大的电感值。

图2 Q(K)和L(K)关于内外径之比K的关系

综合品质因子和电感来看，K在0～0.3之间结果都比较理想，0.05～0.2时取值最优。因此，在外径R2足够小和绕线工艺允许的前提下，应尽可能使K达到0.05～0.2的最优范围。

1.2.2 线圈厚度的优化分析

由式(12)和式(13)可知，线圈的Q值和r0成正比，线圈的电感L和r0的平方成反比。虽然r0越大Q值越大，但是越粗的导线在高频率的交流电下会产生比其直流电阻还要大很多的交流电阻[11]，从而产生误差，r0增加导致L下降更会影响测量细微阻抗变化量的精确度。所以应该用更细的导线来减小厚度。

由式(12)、式(13)可知，线圈的Q值和匝数N成正比，线圈的电感L和N的平方成正比。在线圈内外径和导线半径固定的情况下，线圈层数与N成正比，所以要在有合适的探测距离的条件下，尽可能增加线圈层数。然而，由于各匝线圈之间的邻近效应，当线圈的层数增加到一定程度，邻近效应将引起巨大的涡流损耗，增大线圈的电阻，减小线圈的电感，从而大幅度降低线圈的Q值[12]。而且当线圈的层数增加时，电感成平方关系增加，线圈各层之间的耦合电容也随之增加，线圈的自谐振频率也将大幅降低，由此使得涡流传感器的工作频率大幅降低，最大工作频率下的Q值也随之降低。

综合L、Q值、灵敏度和自谐振频率等多个因素来看，对于探头直径较小的线圈，应采用更薄的线圈。

1.2.3 线圈激励频率的优化分析

电涡流传感器的线圈和被测体之间的耦合关系类似于变压器模型。线圈是电阻和电感串联，输入一个交流信号的变压器初级，被测体是电阻和电感串联的短路次级[13]，定义常数S，在平面线圈涡流传感器中，表达式为:

S越大，传感器灵敏度越高，温度稳定性越好。由上式可以得出提高被测体电导率σ和激励频率f可以增加灵敏度和温度稳定性。

2 仿真模型建立

2.1 理论基础

麦克斯韦方程组概括了所有宏观的电磁现象的规律，因此各种电磁现象都可以用特定条件下的麦克斯韦方程组来描述[14]。这种电磁场满足的微分方程组为:

满足边界条件:

2.2 被测对象的确立

由上文可知，要提高涡流传感器的性能，就要尽可能的提高被测体的电导率和工作频率。实际中，目标导体的电导率可提高的空间很有限，在常温下，铜和铝是最好的选择。纯银的电导率虽然最高，但其价格昂贵，而且容易氧化变质，因此在实际中并不采用。主要使用的目标仍然为铜。

2.3 参数化建模

采用最新版本COMSOL Multiphysics 5.3a的2D轴对称模型，AD/DC磁场求解，频域研究和瞬态研究。线圈精密缠绕，之间的间隙很小，所以采用线圈一体化建模，误差小效率高，大大提高了计算效率的同时精度也得到保证。

通过参数扫描的方式，可以方便地计算出一系列参数下的涡流传感器电感变化[15]，方便计算和对比结果。比如改变内径大小、线圈厚度、激励频率和匝数等一系列梯度值，获得该线圈的响应曲线和变化率。模型如图3所示。

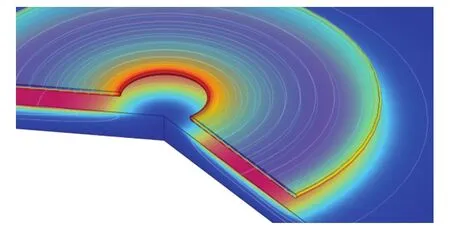
图3 电涡流传感器模型图

在瞬态研究定义温度，分别对0～100℃之间每隔20℃进行参数化扫描，分别对不同激励频率进行仿真。

2.4 优化网格划分

传统建模的网格划分只是对整个模型进行用户控制网格划分，并没有精确到各个域，如图4(a)。本文对计算精度要求很高，截面积很小线圈和被测体模型域采用最大单元尺寸为0.1 mm的自由四边形网格进行划分，对精度要求不太高的空气域采用最大单元尺寸为0.4 mm的自由三角形网格进行划分。这样既保证了计算的精度，又降低了计算量。通过针对性的分块划分网格对线圈和被测体进行优化，如图4(b)。

图4 网格划分优化前后对比

3 仿真结果分析

3.1 合理性分析

因为传感器线圈的直径越小越好，那么就要保证在外半径足够小的前提下，通过改变其他参数来尽可能提高位移灵敏度和分辨率。所以设置传感器模型中铜线圈外半径2.5 mm不变，内径0.5 mm，导线半径20 μm，单层40匝，与非铁磁性被测体目标(铜、铝)距离0.2 mm，激励频率为100 kHz。通过参数化扫描，可以改变其中意参数为一系列的梯度值，方便计算和对比结果。

被测体中横向和在线圈平均半径下的纵向涡流分布如图5所示。涡流集中在线圈内径和外径之间的范围，并在内外半径之间呈轴对称状态，在平均半径处达到峰值。

图5 涡流强度在被测体横向的分布

在线圈平均半径下纵向涡流分布如图6所示。在深入导体内部后快速衰减，因为二次涡流效应，会出现负值，之后趋于0，证明此模型的合理性。

图6 涡流强度在被测体纵向的分布

3.2 线圈内半径的选择

在线圈外半径2.5 mm不变时，不同内半径下的归一化电感与位移的变化曲线如图7所示，K＝0.04和K＝0.2这两条曲线几乎完全重合，归一化电感变化率较大，且在位移与外半径之比为0.04～0.10之间电感变化最快，此时对应的位移为0.1 mm～0.25 mm。当K＝0.4和K＝0.8时归一化电感变化率降低7.5%和13%，不适合做高精度位移传感器探头的理想参数。

图7 不同内半径下线圈归一化电感和位移的关系

3.3 线圈厚度的选择

线圈厚度对线圈电感的影响如图8所示，电感在厚度小于0.1 mm时保持最高值，随着厚度增加而减小，但是减小的幅度比较小，小于1 μH。Q值变化的幅度也不够大。

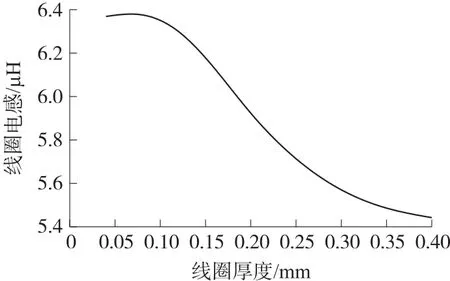
图8 线圈厚度与电感的关系

因为位移在0.1 mm～0.25 mm时电感变化最快，所以继续比较位移在0.1 mm～0.2 mm时电感变化率随厚度的变化，如图9所示，虽然在厚度为0.08 mm时电感值最大，但是电感变化率却下降了14%，故最佳厚度应不超过0.04 mm。

图9 线圈厚度与电感变化率的关系

3.4 线圈匝数的选择

由式(6)可得线圈电感值和匝数的平方成正比，可知增加匝数可以显著提高线圈的电感量。如图10所示，改变纵坐标的刻度值从而更好的显示电感值和匝数平方之间的关系。

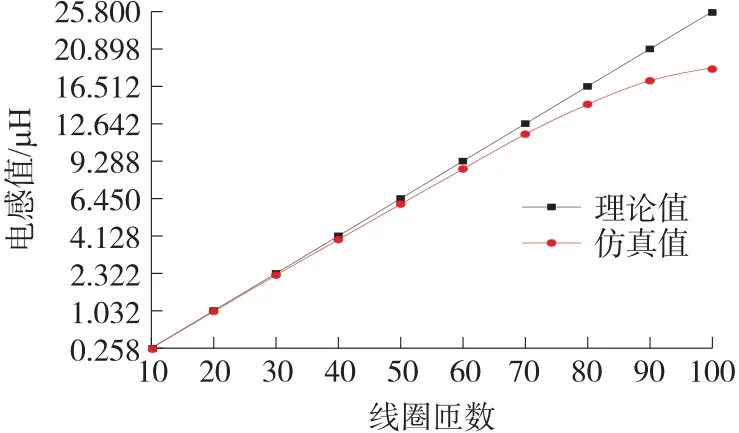
图10 线圈匝数和电感的关系

仿真电感值衰减是因为各匝线圈之间会存在邻近效应，随着匝数的增加，邻近效应会引起巨大的涡流损耗，增大线圈电阻，减小线圈电感，由图可知当线圈匝数为100匝时电感仿真值比理论值下降了15%，线圈的自谐振频率大幅下降，从而使涡流传感器的工作频率也大幅降低，因此匝数不宜选用过大。

图11为位移0.1 mm～0.2 mm时匝数和电感变化率之间的关系，可知当匝数为60匝时电感变化率比其他匝数提高了10%～20%，灵敏度最高。

图11 线圈匝数和电感变化率的关系

3.5 激励频率的选择

设定线圈和被测体之间距离为0.1 mm和0.2 mm，激励频率从100 kHz到1 MHz，记录每个频率点时的电感差值ΔL，由图12可以看出激励频率和电感变化率成正相关，到900 kHz时增长率开始变缓，因此理论上激励频率最好在900 kHz以上，越大越好。

图12 激励频率和电感变化率的关系

尽管随着激励频率的提高电感变化率会增加，材料引起的误差下降，一定程度上提高了传感器的灵敏度，然而激励频率的增加意味着设计电路部分的功耗增加，这对于便携式，低功耗的传感器来说是十分不利的，而且激励频率的增加会导致温漂加剧，从而影响测量结果的准确性。

目前的仿真研究是在293.15 K恒温稳态条件下进行，为了研究激励频率和温漂的关系，本文在稳态模型中加入瞬态温度模块，在位移和频率随着温度变化之间寻求最小电感变化率从而降低温漂带来的误差。这样能把抑制温漂的效果最大化。令传感器的探头线圈结构参数保持不变，检测距离为0.1 mm和0.2 mm，温度从0～100℃之间以20℃为间隔依次变化，在900 kHz和1 MHz下电感变化率受温度和检测距离的影响如图13所示。

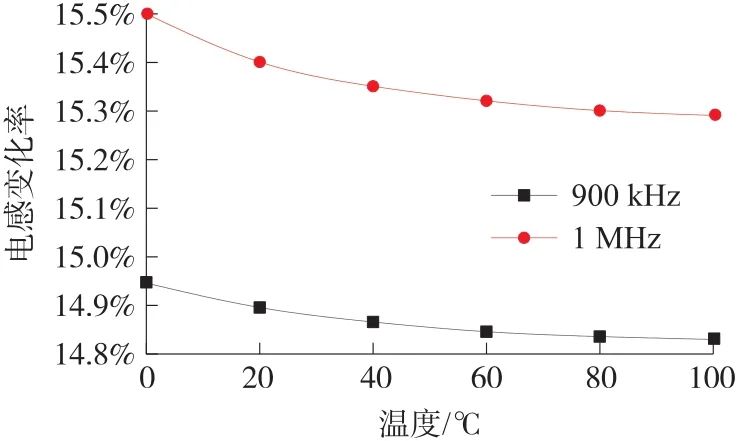
图13 温度和电感变化率的关系

由图可知，100℃内，900 kHz频率下电感变化率波动比1 MHz时下降了45%，因此选用900 kHz激励频率在保证电感标化率足够高的基础上最好的抑制温漂，最大限度的提高线圈的精度和稳定性。

4 实验分析

4.1 传感器实测

本实验首先采用直径40 μm、内半径0.1 mm、外半径2.5 mm的60匝单层漆包线圈和半径5.5 cm，厚度0.5 cm的圆形铜板被测体，固定在在ZA-JY02型高精度位移静校台上，然后将同惠TH2838LCR测试仪的探头和线圈连接，使用热烘干箱控制温度。测量示意图如图14所示。

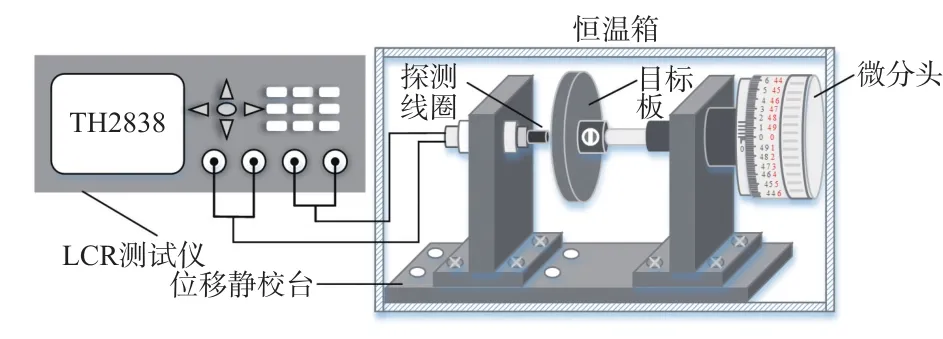
图14 传感器测量图

4.2 实验结果

设置线圈和被测体的距离分别为0.1 mm和0.2 mm，LCR测试仪的激励电流为20mA，激励频率分别为900 kHz和1 MHz，热烘干箱温度在0～100℃之间以20℃为间隔依次变化，记录每次变化的电感值。为减小测量误差，每组测量5次求平均电感值，测量结果如表1所示。

表1 不同激励频率下电感变化率随温度的变化

从表中可以看出，当激励频率为1 MHz，温度在0～100℃变化时，电感变化率最大波动范围是0.31%，而当激励频率为900 kHz时，电感变化率最大波动范围是0.11%，受温度的影响明显下降，和仿真结果一致。因此可以得到激励频率在900 kHz时抵御温漂误差的能力更强，热稳定性更好。

5 结论

本文提出了一种通过电感变化率优化线圈参数和激励频率的方法，综合考虑灵敏度和热稳定性，通过有限元软件COMSOL仿真获得了电感变化率最高时的线圈参数和激励频率，在高灵敏度的激励频率下改变温度，通过实验得到了电感变化率受温度影响较小的最优激励频率，减小了温漂误差。此外，本文的优化思路和结论对后续获得大幅度的位移电感变化曲线也具有一定的参考价值。