基于遗传算法的时栅误差参数辨识与补偿方法研究∗

郑方燕，颜 路，汤其富，郑 永，简圣杰

(1.重庆理工大学机械检测技术与装备教育部工程研究中心，重庆400054；2.重庆商务职业学院公共管理系，重庆401331)

磁场式时栅角位移传感器是根据“时-空坐标转换理论”研制的一种磁感应式角位移传感器，通过对时间的测量实现了角位移的空间测量[1-2]。在测量过程中，因机械结构、电气特性、控制系统及信号处理电路等环节都会引入误差且存在误差累积和逐级放大问题，使得传感器呈现出较低的原始测量精度以及测量系统末端误差成分复杂等特点[3-4]。

国内外学者在角位移测量误差处理与测量精度优化方面进行了深入研究，Hwang S H等人[5]针对旋转变压器信号幅度不均和信号不完全正交对传感器带来的误差影响，通过d-q电流方法进行补偿，取得了良好效果，但此方法需要消耗大量计算时间，且存在因实时性不够好而带来的截断误差。K K等人[6-7]提出利用插值方法对莫尔条纹信号进行数字化细分来提高测量系统的分辨率与精度，但在高次幂逼近时会产生龙格现象，使得逼近极不稳定。韦芙芽等人[8]采用粒子群参数辨识方法对参数函数方程中的待定参量进行辨识，进而通过辨识模型来补偿编码器细分误差，此方法具有可靠性高、环境适应度强、实时响应快和补偿精度高等优点，但是该算法要求模型必须为分数阶系统。高旭等人[9]利用经验模态分解(EMD)算法提取与基波时域频率匹配的本征模态函数包络分量，抑制原始信号的谐波分量，以改善传感器的信号质量，此方法具有测速稳定性高，抗干扰能力强等优点，但是此方法在应用时必须建立起其对应的本征函数模型，且存在适用条件非常苛刻的缺点。如前所述的精度优化与误差补偿算法的应用对象均为光栅或旋转变压器等直接解算空间位移类型的传感器，其实现过程可总结为:利用具体模型特征进行相关函数或模型参数的归一化抽象处理，并在优化算法模式化的处理过程中设置具体参量和约束，最后进行模型演算或迭代训练进而得到输出结果。然而针对时栅传感器的误差补偿算法，仍有少量的研究。彭东林等人[10]采用FFT变换及谐波修正方法对误差进行辨识和补偿，实现了传感器的高精度测量。但此方法要求传感器具有较高的稳定性和匀速性，且受原始测量精度的影响，在更高精度场合的应用受到限制。刘小康等人[11]利用高速FPGA和ARM处理器进行高速信号采集，再利用时钟插补方法对信号进行细分来消除误差提高精度，此方法对特殊场合的动态测量信号进行辨识与细分方面取得了较好的效果，但此方法对CPU性能和FPGA的信号采集频率要求较高。

针对上述问题，本文从时栅传感器的误差成分出发，提出一种利用遗传算法(GA)的误差参数辨识和补偿新方法。以MATLAB2015b为算法和模型仿真工具，选取实际的采样数据为训练样本，进行误差参数的优化和结果输出，通过对误差补偿最终实现传感器系统精度的大幅度提高。

1 时栅传感器原理与误差分析

1.1 时栅传感器原理

时栅传感器的结构和传感原理如图1所示。传感器由动子和定子组成，动子与定子相对放置。动子齿槽内绕制空间互差90°的励磁线圈，当在励磁线圈中通以时间互差90°的交流激励e1(t)和e2(t)时，即可获得四路磁通密度 BT1、BT2、BT3、BT4。 其中BT1、BT3由 e1(t)产生，BT2、BT4由 e2(t)产生。 定子采用PCB工艺印制有相位互差180°正弦型磁场拾取线圈。根据法拉第电磁感应定律，定子磁场拾取线圈会形成两路磁通 φ1，3、φ2，4，如式(1)、式(2)，并由此在拾取线圈内部产生感应电动势 E1，3、E2，4，如式(3)、式(4)。

图1 时栅传感器原理图

设激励信号幅值a＝b，将式(3)、式(4)相加，即可得如式(5)所示的行波信号 E(t，θ)。 E(t，θ)的相位与角位移θ呈正比例关系，因此通过检测E(t，θ)信号的相位量就可确定动子相对于定子转过的角位移量θ[12-13]。

式中:k为动子线圈电磁转化系数；r为拾取线圈中心线半径；Δh为磁场拾取线圈正弦结构幅值；NP为励磁线圈和拾取线圈线的线圈结构数。

设激励e1(t)、e2(t)的幅值相等，即 a＝b，将式(3)、式(4)相加，即可得:

1.2 误差分析

根据时栅传感器的测量原理，经磁-电耦合得到的行波信号的质量直接影响角位移的测量精度[14-16]。因此，线圈结构参数不理想以及交流激励e1(t)和e2(t)的幅值不等等情形都将影响行波质量，从而降低测量精度。前述式(5)所示，令，拾取线圈上得到的感应电动势可简化为式(6)、式(7)。

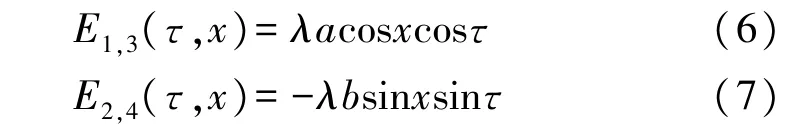
将式(6)、式(7)相加即得到行波信号为:

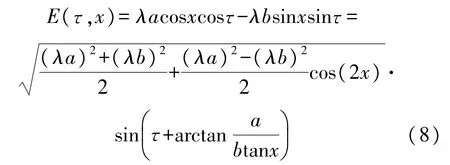
当a＝b时，两路驻波合成列标准行波(式(5))。

当a≠b时，由式(8)可知，信号幅值会由cos(2x)引起一个二次分量，根据时栅测量原理，这个二次变化必然会在测量结果中引入一个二次误差。且波动峰峰值为

当两路激励信号的幅值相等而存在微小相位偏移量Δφ，即驻波相差不为90°。根据式(8)可推导出式(10):

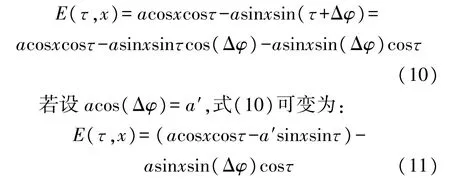
因为a≠a′，括号部分可看作幅值不相等的两路驻波相加。由前面分析可知，会引入一个二次误差，而后半部分因sin(Δφ)是一个微小量忽略不计。

因磁场分布不理想使线圈感应出的调制信号中存在高次谐波成分，则此时得到的行波信号表达式如下:

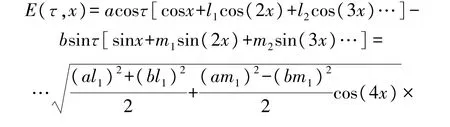
由式(12)可看出，引入了四次误差成分。

为了验证和分析测量误差的谐波成分，采集了传感器一个对极内的500个实测误差数据并做出如图2所示的频谱图。从图中可以看出，测量结果中主要存在二次和四次误差。根据前面的分析，二次误差主要由线圈结构参数不理想以及交流激励e1(t)和e2(t)的幅值不等、相移等情形引起的；四次误差则由磁场的分布不理想造成的。

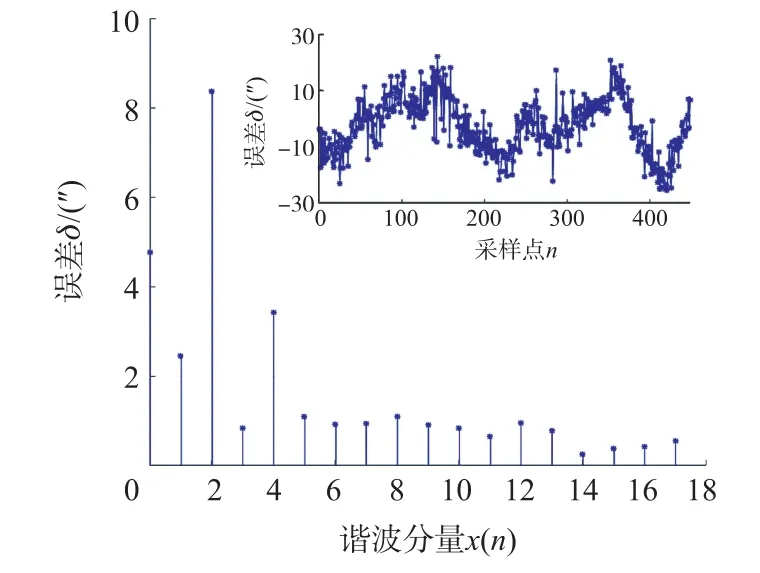
图2 样本数据频谱图

2 遗传算法研究与辨识模型建立

根据前述误差分析结果建立起的时栅传感器的误差函数为式(13):

式中:ysin、ycos表示正弦和余弦误差分布曲线，pk、qk表示相位不等偏差，ω为角频率，Ak、Bk表示谐波幅值，Aksin(kω＋pk)、Bkcos(kω＋qk)表示正弦和余弦性谐波分量。

由式(13)所示，传感器测量误差与 Ak、pk、Bk、qk相关，由此建立基于遗传算法的参数辨识模型。

2.1 时栅的GA模型建立

由式(13)可知，不同参数有其相对确定的取值范围和对应辨识GA模型。作者用不同频次误差参数建立相适应的GA目标函数，进而分别在GA模型中对误差参数样本数据进行训练优化，最终建立起含有误差参数的正、余弦的方程组。

GA主要包括三种算子:选择、交叉、变异。其中选择即再生、交叉即重组、变异即个体基因变动[17]。

具体建模流程如图3所示，算法寻优过程如下:①对时栅样本数据进行二进制编码；②采用轮盘赌方式随机产生初始训练样本M，并定义适应度函数；③评价群体，计算目标函数，进行适应度判断；④遗传操作(选择、交叉Pr、变异Pm)产生新群体Pm≤Pr；⑤重复执行步骤③和步骤④，直到满足停止规则。

图3 基于遗传算法的辨识与补偿建模流程

2.2 参数辨识模型建立

分析时栅误差数学模型，模型中的每组参数Ak、pk、Bk、qk可以从模型的相关参数得到映射关系，并以此建立适合时栅的GA误差参数辨识模型，即将时栅二次误差、四次误差与建立的辨识参数模型中的误差参数进行函数映射，函数公式如下:

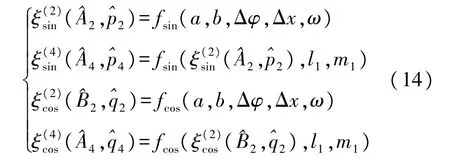
用实际采样的传感器数据确定的 Ak、pk、Bk、qk几个参数的值作为真值，再与GA模型求得结果进行对比分析和误差补偿。

2.3 模型辨识仿真过程与优化

①目标函数建立

当目标函数Jsin和Jcos达到最小值时，误差参数估计函数与实验采样真实函数的谐波分量和之间的差值最小，进一步抽象为求的模和差的模，如式(16)。 对A＾i、p＾i、B＾i、q＾i的参数范围进行确定:幅值参数不超过基波幅值的15%，相位参数范围取0～2π。则仿真模型值y＾sin、y＾cos可以表示为:

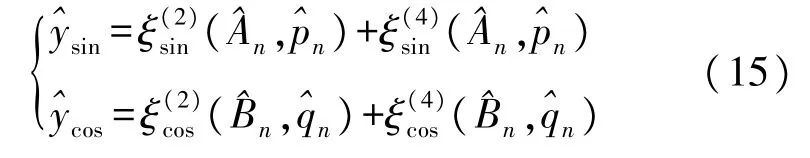
式中:＾Ai、＾pi、＾Bi、＾qi参数由a、b、Δφ、Δx、ω来选取确定，得到目标函数组Jsin、Jcos的表达式为式(16):

②初始种群及编码

种群规模σ直接影响GA的性能与效率，一般设为20～200，本文选取的σ＝90。编码采用二进制编码。

③解码和适应度函数

解码按编码的逆过程进行。适应度函数由目标函数映射而得，要满足单指、连续、非负以及计算量不宜过大则适应度函数采用目标函数倒数形式为[18]:

式中:ε1是为防止发生溢出设置的常量，ε2是变换系数，防止 Fcos、Fsin计算值过大，实际取值 ε1＝0.002，ε2＝0.3。

④遗传算子的确定

ⓐ选择运算:轮盘赌方式即各个体被选中的概率与其适应度大小成正比。

ⓑ交叉算子:交叉概率Pr控制交叉频率，交叉概率与种群更新呈正相关。交叉概率一般取0.5～0.8。 在本文 Pr＝0.8。

ⓒ变异算子:变异概率Pm影响算法性能，主要体现为局部随机搜索能力，一般在0.001～0.1之间，本文 Pm＝0.03。

ⓓ终止条件:当整个种群收敛，即每个个体的适应度相等，就认为此时整个进化过程可以结束，设置适应度误差为0.01，设置最大代数的限制为200代，即满足以上任何一个条件就停止进化。

2.4 辨识结果与模型验证

为了得到 Ak、pk、Bk、qk，首先从 a、b、Δφ、Δx、ω 中分别选取50个实际数据为样本，并采用轮盘赌方法确定四组误差参数A2＝10.137 6和P2＝1.178 1、A4＝1.750 6和 P4＝4.285 1、B2＝18.87 2和 q2＝4.145 1、B4＝1.654 2和q4＝3.745 1为真值，然后根据式(14)建立的误差参数GA模型迭代逼近。迭代结束条件设置适应度相等、迭代次数小于200代、迭代序列收敛与真值误差在±0.01之间小于10代，三者只要满足其中之一即迭代结束。

对于图4和图5表明在初始样本相同的条件下，进行GA迭代的正弦性和余弦性优化跟踪曲线，从图中可以反映出，随着迭代次数增加其个体适应度也会增加，继而在适应度最大的样本域中利用其训练的误差参数所辨识的样本误差最小。

图4 正弦遗传算法优化跟踪曲线

图5 余弦遗传算法优化跟踪曲线

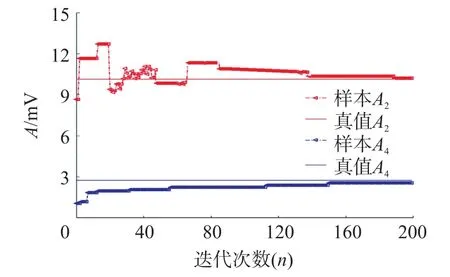
图6 参数A辨识曲线

图6为正弦性误差辨识参数A2、A4经过GA迭代后的逼近曲线。由图6可知，A2在0～80代时，存在迭代收敛趋势不明显，由于GA的健壮性和自适应性，在80代以后曲线呈现出逐步收敛于真值10.137 6的趋势；A4从一开始就呈现出明显的收敛趋势，并于真值2.810 5附近迭代停止，仿真结果显示，收敛逼近值为10.427 9和2.819 7，均满足数据的理论范围10.113 2～11.012 1和2.532 1～3.001 2。

图7为余弦性误差辨识参数B2、B4经过GA迭代后的逼近曲线。由图7可知，两条曲线迭代一开始就呈现出较好的收敛趋势，两参数最后分别在140代和180代于真值18.872和1.654 2附近迭代停止，仿真结果显示，收敛逼近值为18.821 1和1.642 7，均满足数据的理论范围18.624 1～19.121 1和1.592 1～1.721 9。

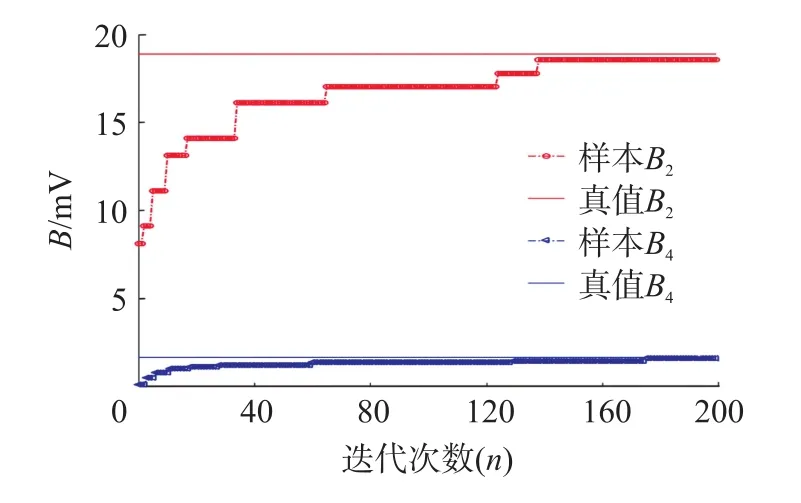
图7 参数B辨识曲线

图8为正弦性误差辨识参数p2、p4经过GA迭代后的逼近曲线。由图8可知，两条曲线存在不同程度的迭代变异比率过大，从图8可以看出主要集中在15～60代之间，因为初始样本利用轮盘赌方式得到，存在个体的差异性，所以在初始遗传迭代时会出现变异和部分交叉概率偏大。虽然初始迭代不稳定，但是GA的自适应性使其能够在最后得到比较好的逼近效果，仿真结果显示，收敛逼近值为1.194 4和4.185 4，均满足数据的理论范围1.162 7～1.315 2和4.012 9～4.241 8。

图8 参数p辨识曲线

图9为余弦性误差辨识参数q2、q4经过GA迭代后的逼近曲线。由图9可知，迭代曲线在初始0～100代均出现比较大的迭代不稳定，但是由于仿真模型的参数设置和GA的特点使整个系统的熵值最终趋于平稳。仿真结果显示，收敛逼近值为4.210 8和3.841 1，均满足数据的理论范围4.013 8～4.211 9和3.473 1～3.997 4。

图9 参数q辨识曲线

表1 正弦参数辨识结果

表2 余弦参数辨识结果

3 补偿结果与实验验证

3.1 实验系统搭建

为了验证GA对时栅误差参数辨识的准确性，搭建试验平台如图10所示。时栅与光栅通过高精度的弹性连接轴同轴安装在四层大理石实验平台上，采用精度为±1″的海德汉ROD886光栅为参考基准，运用XILINX可扩展处理实验平台Zynq-7020进行数据采集和算法求解。在该实验平台的基础上，展开精度实验以及本文提出的基于遗传算法的时栅信号处理方法和传统时栅信号处理方法的对比实验。

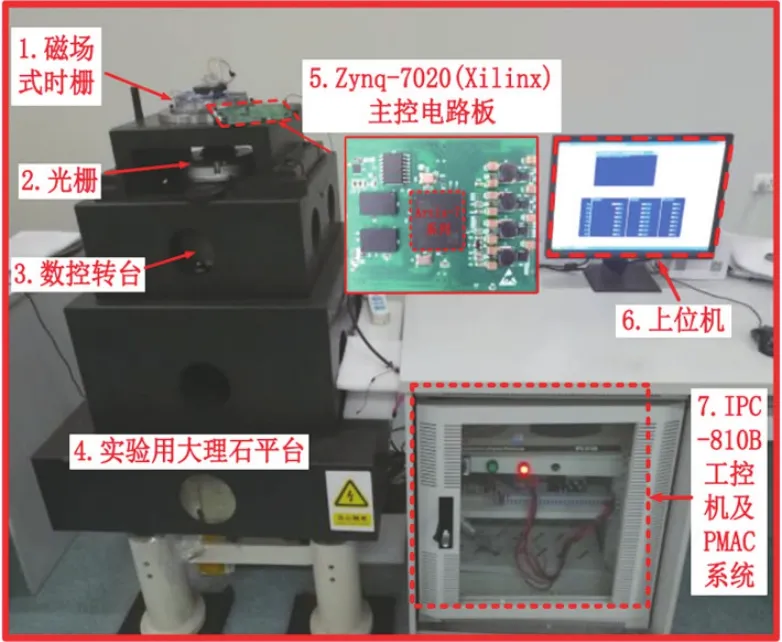
图10 实验系统

3.2 补偿方法

依据时栅传感器的GA模型(式(13))，建立起的补偿数学模型如式(18):

式中:ysin、ycos表示采样点初始采样值，Ysin，Ycos表示采样点的补偿后的值，＾Ak、＾Bk、＾pk、＾qk为模型参数辨识结果，ω为输入交流激励e1(t)和e2(t)角频率。

3.3 精度实验

为了验证基于GA的误差补偿方法的有效性，在传感器360°整周范围内采集未使用和使用此方法的两组数据，两组数据具有相同测量点且均为整周采样。图11为未使用GA方法的数据误差曲线，误差峰峰值为57.3″，图12为使用GA方法补偿后的整周误差曲线，误差峰峰值为17.3″从图中可以看出周期性误差明显减少，曲线更趋于平缓。为了更直观的对比两组数据，将得到的两误差曲线置于同一图中，如图13所示。将明显减少的整周误差量数据整理为如表3所示。同时，分别作出两组数据的频谱图，如图14所示。由图中可以看出二次、四次误差明显减少，减少量分别为66.67%和54.05%，如表4所示。

图11 整周误差数据分布

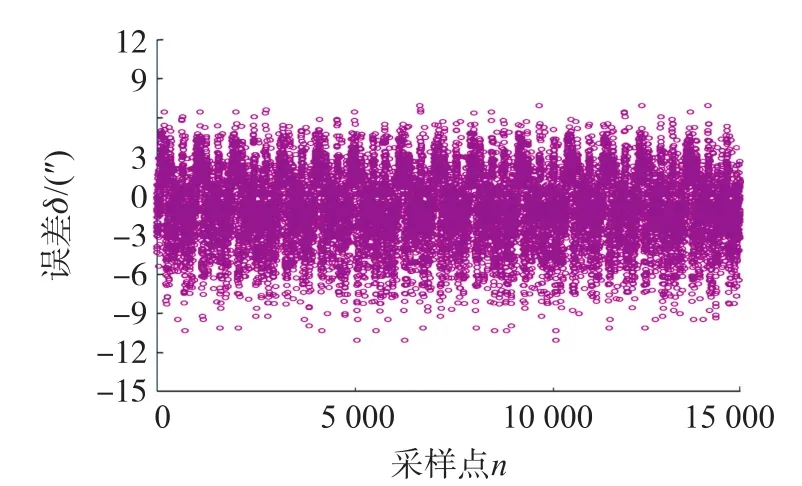
图12 GA处理后整周误差数据分布

图13 整周采样点误差数据对比波形

图14 样本数据频谱对比图

表3 整周误差补偿前后对比

表4 不同频率成分误差减少量

3.4 精度对比实验

对比实验是采用灰色算法和指数平滑法，在360°整周范围内进行相同测量点采集数据的预测分析，与GA方法进行误差补偿效果对比，实验数据如图15和图16所示。灰色算法处理后时栅传感器整周测量误差峰峰值为46.8″，指数平滑法峰峰值为32.1″，并且选取灰色算法和指数平滑法处理后的一个对极内500个数据进行频谱分析，如图17和图18所示，灰色算法和指数平滑法对其高频成分有一定抑制，但是对影响磁场式时栅测量精度的二次误差、四次误差抑制效果不明显，且指数平滑法还会带来明显三次误差。

图15 灰色算法处理与原始误差数据对比

图16 指数平滑法与原始误差数据对比

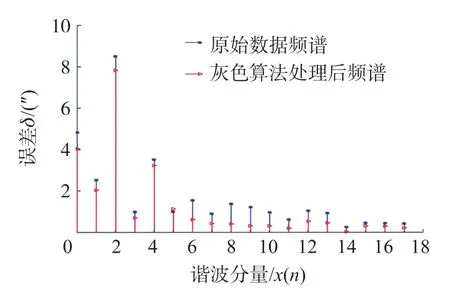
图17 灰色算法处理后的频谱

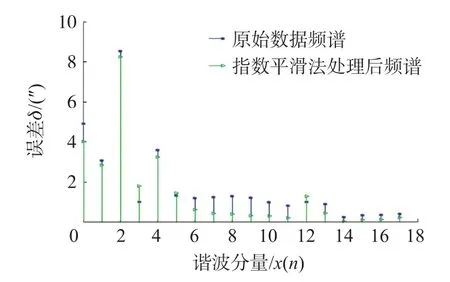
图18 指数平滑法处理后频谱

4 结论

针对磁场式时栅传感器原始测量精度低的问题，本文提出了一种基于遗传算法的应用于磁场式时栅的误差参数辨识与补偿方法。通过理论分析和实验研究可知:①采用基于GA的误差处理方法对时栅误差进行参数辨识和补偿，可以有效减少时栅位移传感器的二次和四次误差，减少量分别为66.67%和54.05%；②采用GA处理方法可以有效降低时栅传感器整周测量误差，误差峰峰值从57.3″减少到17.3″，从而提高了传感器原始测量精度。

以上研究，揭示了磁场式传感器的误差特性并对原始信号进行了有效补偿，为进一步深入开展该项研究提供了研究基础。该项研究可应于同类型的电场式时栅、光场式时栅、感应同步器以及旋转变压器等位移传感器。