基于改进Landweber算法的ECT图像重建∗

严春满，穆 哲，张道亮，陆根源

(1.西北师范大学物理与电子工程学院，兰州730070；2.甘肃省智能信息技术与应用工程研究中心，兰州730070)

电容层析成像(Electrical Capacitance Tomography，ECT)技术具有无辐射、响应速度快、结构简单、非接触等优点，因而在多相流检测领域获得了广泛应用。ECT系统主要包括传感器、数据采集及图像重建单元，其中图像重建较为关键，是系统能否成功应用到工业实践上的关键技术之一[1]。

图像重建的主要原理是根据所测得的电极对之间的独立电容值，计算出相应的灵敏度矩阵，再通过一定的图像重建算法，重建出管道内流体截面图形[2-5]。依据算法主要原理，可将图像重建算法大致分为三类:直接法、迭代法及智能算法。线性反投影算法(LBP)是直接法中较典型的代表[6]，该算法采用灵敏度矩阵的转置代替逆矩阵进行成像，具有计算量小、速度快等优点，但重建图像的质量不理想。迭代法主要包括Landweber算法[7]、共轭梯度算法(CG)[8]等。迭代类算法相对于非迭代类算法具有较好的成像质量，但是随着迭代步数的增加，算法的实时性受到一定的影响。智能算法主要包括神经网络算法等[9-10]。由于神经网络可以建立输入与输出数据的非线性映射关系，因此可以应用于求解ECT图像重建的问题中，然而神经网络需要大量的训练样本，且由于多相流的复杂性，训练样本的获取并不容易。

在各类算法中，Landweber算法在重建质量及速度方面具有较好的折衷性，该算法相对于直接算法有着较高的成像精度，且算法复杂度不高。经典Landweber算法的主要缺点是:存在着半收敛问题，针对不同流型为了获得最佳重建图像所需要的迭代次数并不一致，对一些复杂流型，为了得到较为理想的重建图像质量所需要的迭代步数往往更大，进而导致图像重建速度较慢[11]。针对算法的主要缺点，文献[12]通过在残差P处添加参数β构造一个新的算子P′，以获取算法的稳定收敛特性，但算法针对不同流型需要设定不同的参数，重建图像的精度不高。文献[13]在经典Landweber的基础上引入Runge_Kutta优化算法，并推导出解决电容层析成像问题的数学模型，有效提高了重建图像的质量。文献[14]提出了改进初值的方法，即引入了阻尼算子并添加一个带参数的单位矩阵，通过参数调节以提高重建图像的质量。文献[15]通过同伦摄动推导出二阶迭代公式并在公式上添加全变差正则项，通过正则化思想提高了重建图像的质量，但依然没有有效解决算法半收敛的问题。

本文在文献[15]的基础上，基于同伦摄动方法推导出二阶迭代公式，并针对二阶迭代公式存在的半收敛问题，通过添加约束因子使谱半径小于1，以有效提高算法的收敛性。为验证改进算法的收敛性及有效性，选择 LBP、Tikhonov、HPIM、原 Landwber算法及四种常见的流型完成了图像重建的对比实验，并对重建图像的主观质量及客观指标做了对比分析。重建图像质量评价的客观指标选取较常用的相关系数及相对误差。实验结果表明，改进算法在重建图像的主观质量上更接近原始流型，在较少迭代次数的前提下，重建图像的相对误差及相关系数优于其他对比算法，实验结果验证了改进算法的收敛性及有效性。

1 改进的Landweber图像重建算法

1.1 Landweber算法基本原理

Landweber迭代算法是由最速下降法演变而来的，它以最小二乘准则为主要依据，是ECT应用领域较为普遍的一种方法。算法的主要原理是在数据残差的负梯度方向上对解进行修正。根据最优化理论，由式C＝SG得到ECT图像重建的极小化目标:

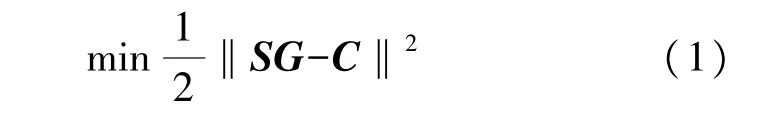
式中:S为灵敏度分布矩阵，G为归一化介电常数分布向量，C为归一化电容向量。

根据向量范数定义，目标函数可写为:

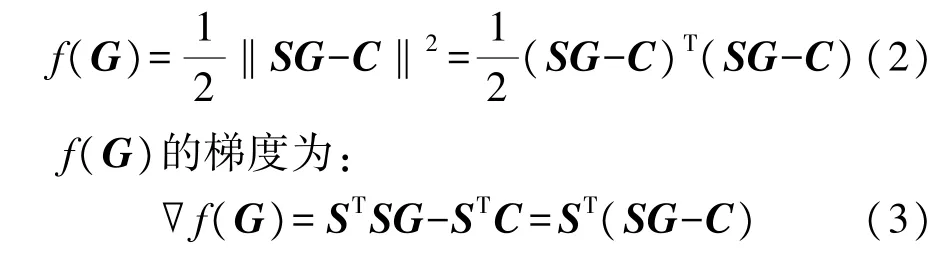
按照最速下降法的原理，将负梯度方向作为优化搜索的方向，则ECT图像重建的迭代公式为:

式中:∂k为最优步长。

1.2 改进的Landweber算法

ECT系统中解决图像重建问题较有效的方法是非线性最小二乘法，即解决式(5)所示的最优化问题:

式中:δ为介电常数分布，Uα为带有噪声的测量电容值，其中α＞0为噪声等级。

式(5)相应的欧拉方程为:

根据同伦思想，构造不动点同伦函数H，R×[0，1]→R且满足:

式中:p∈[0，1]为嵌入同伦参数，v为方程(7)的解，δ0为介电常数分布的初始值。

假设式(7)的解可以展开成关于p的幂级数:

当p→1时，式(7)与式(6)等价，则可得到式(6)的近似解:

将式(7)中的F(v)在δ0处进行泰勒级数展开并忽略高阶项，可以得到:

将式(8)代入式(10)可得到:

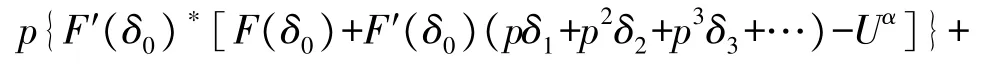
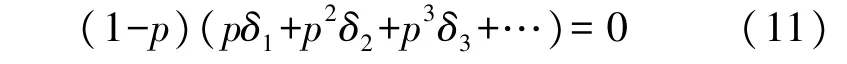
按照p的不同幂次进行同类项合并得到:

根据以上形式，构造两种迭代形式:

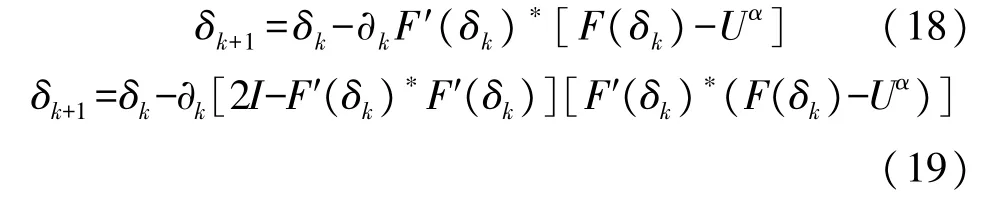
式(18)为经典的Landweber算法迭代公式，而式(19)则是二阶近似Landweber迭代算法(Homotopy Perturbation Iterative Method，HPIM)，即同伦摄动反演方法。

根据以上分析可知式(6)的解可进一步写为:

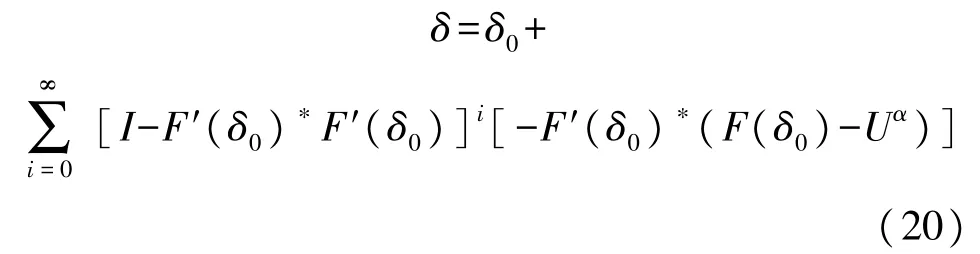
令 R＝I-F′(δ0)∗F′(δ0)为残差，仅当残差的谱半径ρ(R)＜1时才能保证级数收敛，而级数半收敛的主要原因为 F′(δ0)∗F′(δ0)不满秩，为解决半收敛问题，利用 F′(δ0)∗F′(δ0)的对称性与非负定性，构造新算子 R′＝μ[I-F′(δ0)∗F′(δ0)]，令 ρ(R′)＝ μ‖[I-F′(δ0)∗F′(δ0)]‖，ζ＝ρ(R)＝ ‖[I-F′(δ0)∗F′(δ0)]‖则:

根据式(21)可见，谱半径ρ(R)存在着大于1的可能，从而影响算法的收敛，因此我们在谱半径处加上约束因子μ，使得ρ(R′)＜1，构造新的迭代公式为:

本文算法具体步骤如下所示:

(1)预处理

①对测量所得的电容值、灵敏度矩阵进行归一化处理；②由LBP算法计算出初始介电常数分布向量；③由预处理实验获取各流型的最优迭代步数、确定约束因子μ；

(2)根据式(22)进行迭代运算；

(3)判断是否满足迭代终止条件，若满足则转至步骤(4)否则返回步骤(2)继续迭代。

(4)输出重建结果。

2 实验及分析

为验证改进算法的收敛性及有效性，本文以两相流为研究对象，选取较经典的 LBP、Tikhonov、Landweber、HPIM与改进算法完成对比实验，其中Landweber、HPIM属于迭代类算法。实验中选取四种常见两相流流型:泡流、核心流、层流以及环流(并依次标定为流型 1、2、3、4)，通过有限元分析软件计算获得电容值及灵敏度矩阵，并完成ECT图像重建。实验中，用64×64的网格将管道截面剖分为4 096个单元，其中3 228个成像单元为该截面的有效区域。重建图像的客观评价指标选取较为常用的相对误差及相关系数。

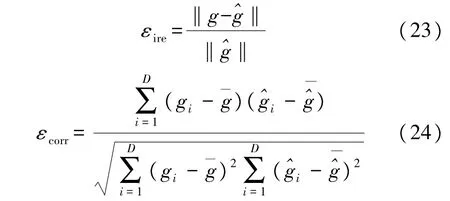
式(23)为相对误差评价指标公式，式(24)为相关系数评价指标公式。式中g表示通过图像重建算法获得的介电常数分布，为管道内真实介电常数分布，分别为g和的平均值，D为g和的维度。依据计算公式，相对误差越小表示重建介电常数分布越接近原始介电常数分布，而相关系数表明原始介电常数分布和重建介电常数分布在统计上的相似性，相关系数越大表示二者越相似，反映重建图像(介电常数分布)质量越高。

2.1 重建图像客观指标对比实验

表1、表2为各对比方法重建的图像与原始图像的相对误差以及相关系数。其中，经典Landweber算法和HPIM算法对流型1、3及流型4迭代次数均为100次，对流型2的迭代次数为200次，本文算法对流型1、2、3以及流型4迭代次数分别为:40次、50次、4次以及35次。

表1 相对误差

表2 相关系数

分析表1与表2数据可见，对于所选四种流型，本文算法的相对误差以及相关系数均优于其他对比算法，且迭代次数要明显少于迭代类算法中的Landweber及HPIM算法。对实验中的四种流型，HPIM算法和Landweber算法在相同迭代次数下对于流型3，所得相对误差以及相关系数差别较小；对流型1、2、4，HPIM 算法略优于 Landweber算法。 在迭代类算法中，本文算法在相对误差及相关系数上均有改善，且对于流型2、3、4，在迭代次数较少的前提下，相对误差的下降与相关系数提高均较为明显；相对于LBP算法及Tikhonov算法，本文算法的相对误差以及相关系数均有明显改善。

实验结果验证了本文算法的有效性，但同时也揭示了迭代次数对算法的影响问题。为进一步验证本文算法的收敛性，我们测试了不同迭代次数对重建图像质量的影响。限于篇幅，这里选取环流(流型4)的实验数据，并将实验结果绘制为图1与图2所示的对比曲线。

图1 环流(流型4)相关系数对比

由图1、图2可见，在初次迭代时(迭代步数为1)，本文算法与Landweber算法、HPIM算法在相关系数和相对误差上几乎相同，但是，随着迭代次数的增加，本文算法能以较快的速度收敛，在迭代35次时就能达到较好的客观评价指标，相关系数高于其他两种对比算法，同时相对误差低于其他两种对比算法。

图2 环流(流型4)相对误差对比

2.2 重建图像主观质量对比

为进一步验证本文算法重建图像的有效性，我们将对比算法所获取的最佳重建图像在表3中做展示。表中第1行为原始流型截面图，第2至6行分别为:LBP、Tikhonov、Landweber、HPIM 以及本文算法的重建流型截面图。

表3 重建图像主观质量对比

由表3重建图像的主观结果可见，LBP算法和Tikhonov算法重建图像发生形变、区分度不佳。原Landweber算法和HPIM算法的重建图像在形状上均大体接近原始流型，主观对比略有差别。相对于其他算法，本文算法能够以较高精度对场域中的各种流型进行重建，尤其是对流型2、3、4，本文算法能够较清楚的重建场域内物体的位置信息和边缘信息，重建图像的物体区分度较好、分辨率较高，且更加接近原始流型。

3 结论

本文对比分析了ECT系统常见的三类图像重建算法，并以Landweber算法为研究重点，阐述了经典Landweber算法的基本原理，分析了影响算法收敛性的主要因素，并针对原算法的半收敛问题，通过同伦摄动方法推导出二阶迭代公式。为解决二阶迭代公式中谱半径影响算法收敛的问题，通过添加约束因子，获得一种全收敛的改进Landweber算法。为验证改进算法的收敛性及有效性，本文以两相流为研究对象，选取四种常见流型:泡流、核心流、层流以及环流，通过较经典的 LBP、Tikhonov、HPIM、Landweber与改进算法完成对比实验。实验结果证明了本文算法的收敛性及有效性，相较于迭代类算法中的HPIM、Landweber算法，在较少迭代次数的前提下，本文算法可获得更高的图像重建精度。