水平管内流动冷凝流型图研究进展
庄晓如 公茂琼 邹 鑫 陈高飞 吴剑峰
(1 中国科学院理化技术研究所 低温工程重点实验室 北京 100190; 2 中国科学院大学 北京 100049)
水平管内流动冷凝流型图研究进展
庄晓如1, 2公茂琼1邹 鑫1陈高飞1吴剑峰1
(1 中国科学院理化技术研究所 低温工程重点实验室 北京 100190; 2 中国科学院大学 北京 100049)
水平管内流动冷凝的两相流型对其传热与流动的研究十分重要,流型图则是流型辨别及其转换判断的重要工具。本文总结了目前水平管内流动冷凝流型图及其转换标准的研究进展,列举了七种针对流动冷凝提出的流型图:Breber et al. (1980),Tandon et al. (1982),Cavallini et al. (2002, 2006),El Hajal et al. (2003),Kim et al. (2012)和Nema et al. (2014),根据现有的研究,发现目前的两相流型图大多针对绝热条件及流动沸腾所提出,其应用于流动冷凝中存在一定的偏差,而流动冷凝两相流型图目前研究还较少。另外,现有的流型图大多针对常规管道和基于常温常压工质所提出,其应用于微管道和低温或高压等工质存在一定的困难,且其研究还未能与传热及压降模型的研究实现较好的联系。
流动冷凝;流型;流型图;水平管
水平管内冷凝传热与流动的研究在能源和化工方面的应用具有重要意义。为了设计出更有效、更经济和体积更小的冷凝换热器,要求寻找更加合适的流动冷凝传热系数预测模型。事实上,流动冷凝的两相流动及传热机理与流型有着密切的关系。Bell K J等[1]曾提出对于不同的流型,应采用不同的传热系数关联式。后来,许多研究也表明基于流型的两相压降和传热模型较一般经验模型更为准确。Kattan N等[2]基于流型提出新的流动沸腾传热预测模型,并发现其相较于一般模型,对高干度(x>0.85)及分层流的传热预测更准确。之后,Wojtan L等[3]进一步对Kattan N等[2]的流型图进行细分和修正,并针对流动沸腾的烧干及雾状流型区域提出新的传热预测模型。El Hajal J等[4-5]基于Kattan N等[2]的流动沸腾流型图提出适用于流动冷凝的新流型图,并提出相应的传热预测模型,将该预测模型与来自九个独立实验室大范围工况下15种工质的2771个实验数据进行对比,得到其对75%的数据预测偏差均在20%以内。对于两相压降的预测,Quibén J M等[6-8]发现现有的模型一般无法应用于全干度范围的预测,提出基于流型的两相压降预测模型,与实验数据进行对比可知,新模型对全干度范围的两相压降预测较好。因此,流型的预测对水平管内流动冷凝的两相流动及传热的研究十分重要。
目前对于两相流型的预测,一般使用二维的两相流型图。在过去的几十年间,国内外的研究者已提出大量不同的两相流型图,其大多针对绝热条件下的两相流动状态。然而,由于传热流动中核态沸腾、沸腾或冷凝热流等方面的影响,传热流型及其转换标准与绝热流动存在明显的差别。例如,流动沸腾中由于核态沸腾的影响,在分层流中加强了液相的湍流流动,使得液膜能更大程度的湿润管内径,加强了气相夹带液滴的含量;核态沸腾还会导致环状流液膜厚度的减小,使得流动沸腾管内壁的湿润周长出现部分烧干现象,产生特有的烧干流型区域(dry flow);由于沸腾或冷凝热流的存在加速或减速了两相流型的变化,导致传热流型及其转换标准的不同[9]。因此,将绝热两相流型图应用于换热(沸腾和冷凝)条件下的两相流型预测存在较大的误差,且沸腾和冷凝条件下的两相流型图也具有较大的差异。本文将针对水平管内流动冷凝的流型图进行总结,并提出研究所存在的科学问题及难点。
1 水平管内流动冷凝的流型分类
图1所示为Palen J W等[10]提出的常规管道典型水平管内冷凝两相流型的分布图。
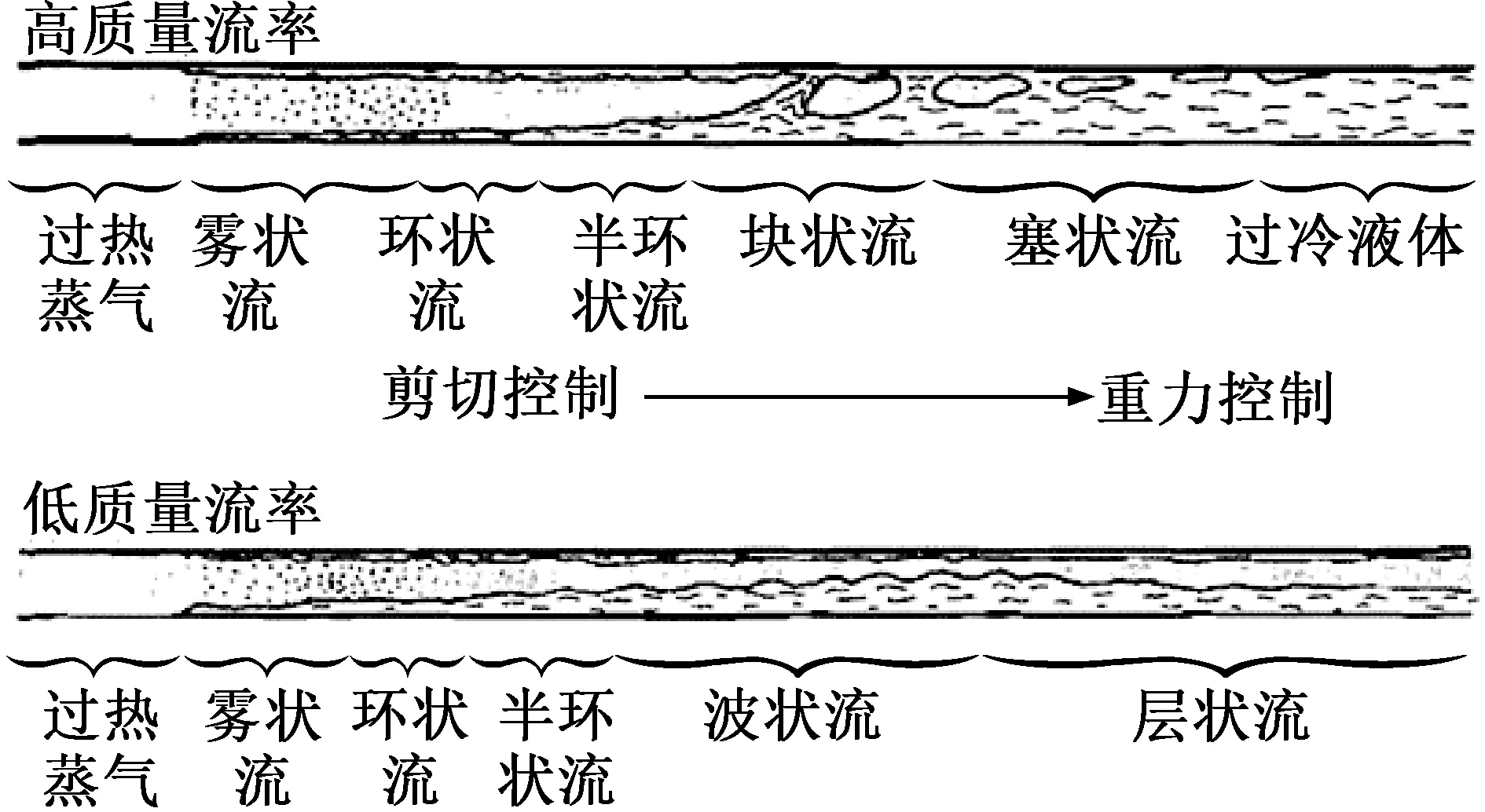
图1 水平管内冷凝两相流型分布图[10]Fig.1 Picture of two phase flow patterns on condensation in horizontal tubes[10]
目前,部分研究认为在冷凝起始,气相流体进入水平管内被冷凝后管内壁会形成很薄的冷凝液膜(肉眼难以分辨),而管中心则出现较多的冷凝液滴,产生雾状流;随着冷凝换热的继续,管内壁的液膜逐渐明显,形成环状流,其气相中心一般也夹带着部分液滴。接着,冷凝液膜不断增厚,由于重力的作用,管底部的液膜会比管顶部厚,形成半环状流。冷凝过程中,流体气相速度逐渐减小,其受气液相界面剪切力的影响减小,受重力的影响则增大。在高质量流率下,由于流体受剪切力的影响仍大于重力,在环状流后会形成块状流和塞状流,而泡状流则只在很低的干度及很高的质量流率下才会出现;在低质量流率下,由于重力的作用,流体液相会大量聚集于管底而形成波状流和层状流。因此,水平管内流动冷凝中出现的流型主要有:雾状流(M)、环状流(A)、半环状流(Semi-A)、块状流(Slug)、塞状流(Plug)、波状流(SW)、层状流(S)和泡状流(B),有的研究会将块状流和塞状流统称为间歇流(I),将波状流和层状流统称为分层流。
2 水平管内流动冷凝流型图的研究进展
目前,两相流型图可分为:经验流型图和理论及半理论流型图。经验流型图是基于已有的实验流型数据发展得到的流型图[11-12],该类流型图具有一定的局限性,一般只适用于特定的工质及工况;理论流型图是通过分析流型转换过程中流体结构变化的物理模型,建立得到各流型转换标准的流型图,其中最具代表性的是1976年Taitel Y等[13]提出的流型图。之后,许多研究者结合实验流型数据在该流型图的基础上进行修改,从而发展得到半理论流型图,在实际应用中对流型预测较好。以下将针对水平管内流动冷凝提出的两相流型图进行总结。
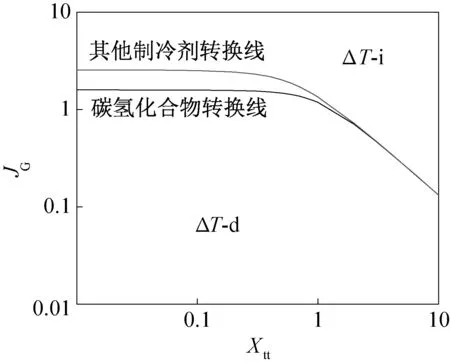
1980年Breber G等[14]将超过700个的实验流型数据与Taitel Y等[13]流型图进行对比,该数据涵盖了大范围的物性及流动特性,发现Taitel Y等[13]流型图对于管内径范围为8~22 mm的数据预测较好,但对于Soliman H M等[15]研究的管内径为4.8 mm的流型预测存在较大偏差,波状流和块状流在Taitel Y等[13]流型图中被预测为环状流,这可能与Taitel Y等[13]流型图中未考虑表面张力对流型变化的影响有关。Breber G等[14]认为Taitel Y等[13]流型图能较好的预测水平管内流动冷凝的流型,但由于其分析较为复杂,应用不便,因此提出了简化的流型图。另外,Breber G等[14]发现实验流型数据中环状流向波状流的转换(Ttransition, 简写为T)并不是突变的,应用一个区域代替一条线做为其转换分界。新的流型图以Martinelli数(Xtt)为横坐标,无量纲气相速度(JG)为纵坐标,具体如图2所示。
(1)
(2)
1982年Tandon T N等[16]在Soliman H M等[17]的基础上提出新的流型图。将管内径范围为4.8~15.9 mm的664个包含工质R12及R113的流动冷凝实验流型数据与新的流型图进行对比发现,环状流和半环状流的数据近似处于同一个区域,因此新的流型图将两种流型归于同一区域。新流型图的纵坐标仍使用无量纲气相速度(JG),而横坐标则使用与两相流型有着密切关系的空隙率函数(1-α)/α,具体如图3所示。
(3)
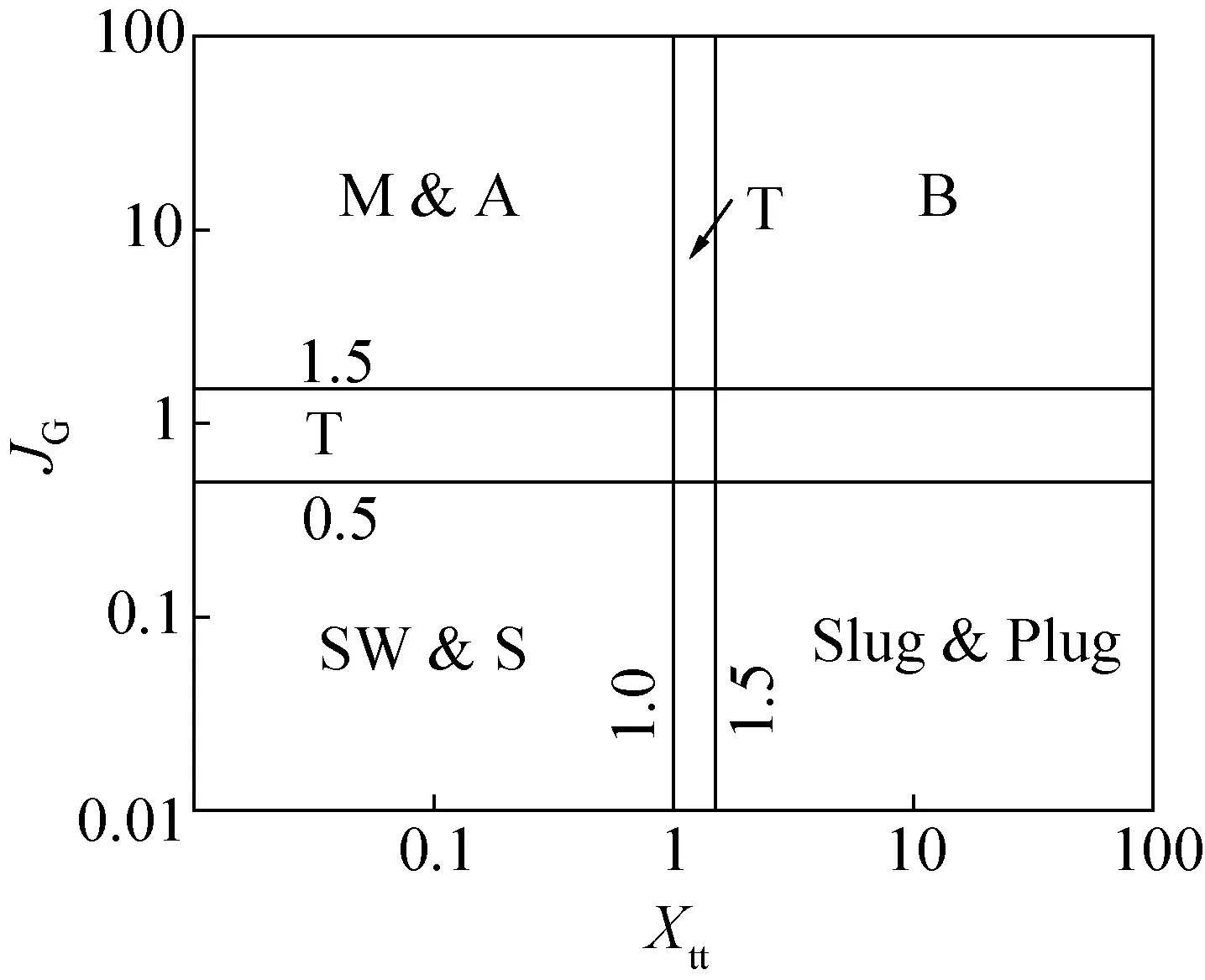
图2 Breber et al. (1980) 水平管内流动冷凝流型图Fig.2 Breber et al. (1980) map on condensation in horizontal tubes

图3 Tandon et al. (1982)水平管内流动冷凝流型图Fig.3 Tandon et al. (1982) map on condensation in horizontal tubes
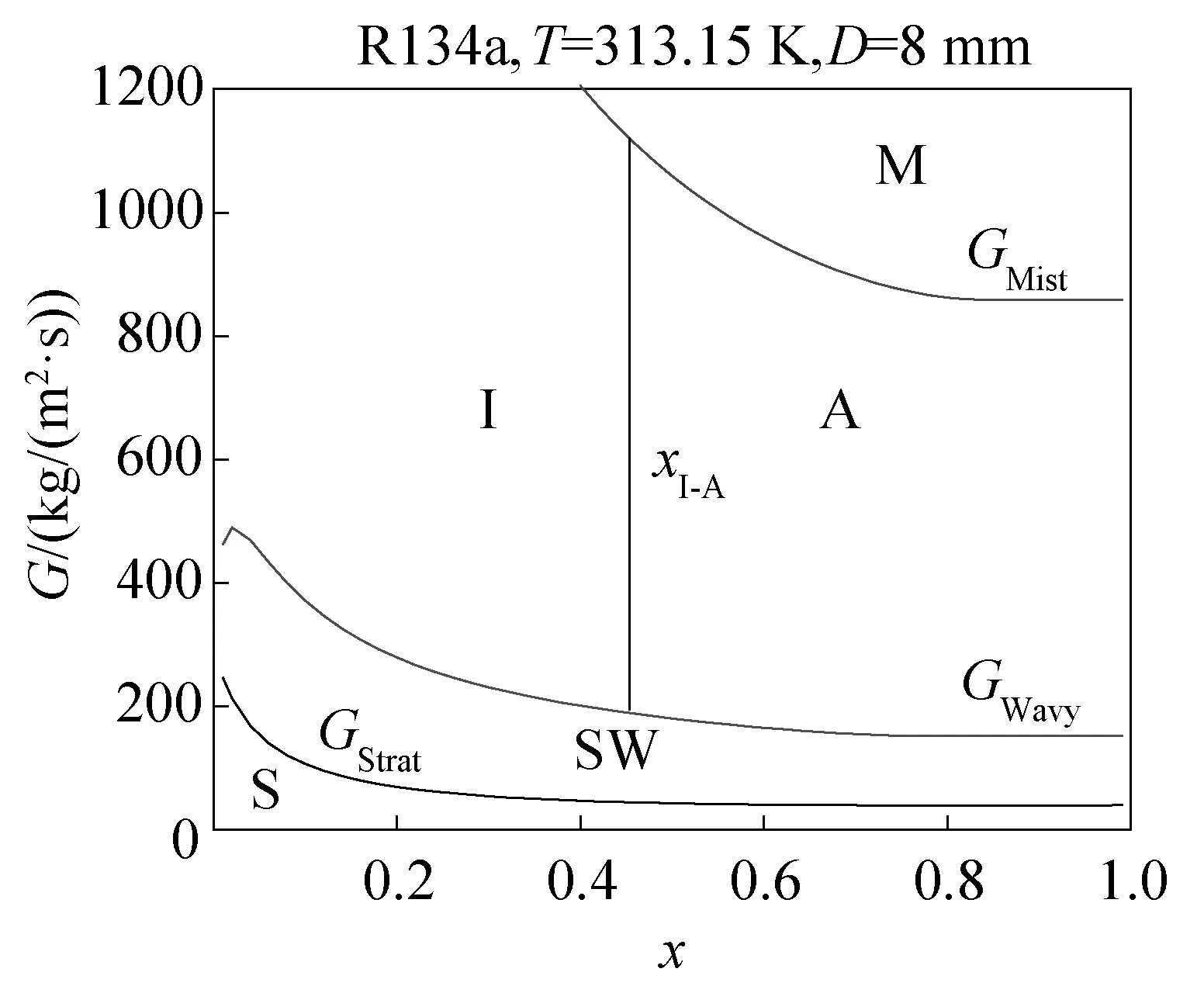
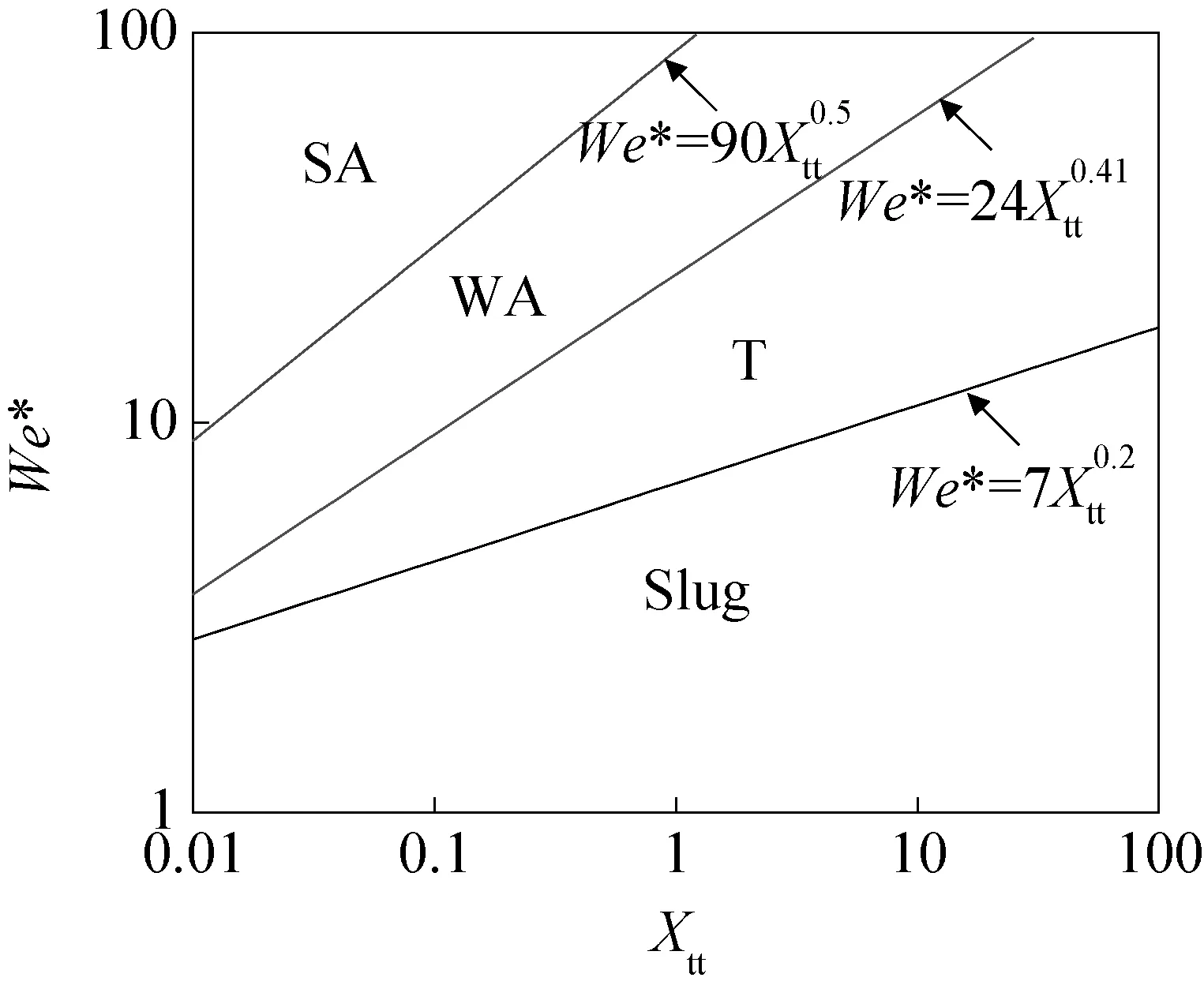
2002年Cavallini A等[18]在工质R22、R32、R125、R410A、R236ea、R134a和R407C,管内径为8 mm的流动冷凝实验数据基础上提出基于两相流型的传热及压降模型,并得到对应的新流型图。该流型图仅将流型分成三类:环状流(A)、块状流(Slug)和过渡区及波状-层状流(T & SW & S),其坐标与Breber G等[14]的流型图相同,具体如图4所示。另外,Rabas T J等[19]和Cavallini A等[18]均指出块状流仅在超过一定质量流率(GW)下才会出现,当G GW=FEρL(gD)0.5 (4) 其中, EF=0.54-0.06Eo2-1.05Eo (5) (6) 图4 Cavallini et al. (2002)水平管内流动冷凝流型图Fig.4 Cavallini et al. (2002) map on condensation in horizontal tubes (7) 式中:对于碳氢化合物,CT=1.6;对于其他制冷剂,CT=2.6。 图5 Cavallini et al. (2006)水平管内流动冷凝流型图Fig.5 Cavallini et al. (2006) map on condensation in horizontal tubes 2003年El Hajal J等[4]基于Kattan N等[21-23]的水平管内流动沸腾流型图,提出了适用于冷凝的新流型图。El Hajal J等[4]发现对于两相流型转换、传热系数和压降均具有重要意义的空隙率,当使用滑移通量模型(考虑了流体两相的径向速度分布)计算时,其对从低压到高压工质的预测,会随压力的增大而过高预测流动冷凝的换热系数;而当其使用均相模型(认为流体气液相的速度相等)计算时,则得到相反的趋势。为了计算适用于不同压力工质的空隙率,El Hajal J等[4]使用了对数平均法,具体形式如下: (8) 式中:αh为使用均相模型计算得到的空隙率;αra为Rouhani S Z等[24]使用滑移通量模型计算得到的空隙率。 (9) (10) El Hajal J等[4]将该空隙率的计算应用于流型图的流型转换标准计算中,得到较好的预测效果。新流型图以干度x和质量流率G为横纵坐标,相关流型转换关联式如下: 1)层状流与波状流的转换关联式: (11) 其中, (12) (13) 2)波状流与间歇流/环状流的转换关联式: (14) 其中, (15) (16) 随着干度的增加,当GWavy达到最小值时,其后将保持最小值。 3)间歇流与环状流的转换关联式: (17) 4)间歇流/环状流与雾状流的转换关联式: (18) 其中, (19) 随着干度的增加,当GMist达到最小值时,其后将保持最小值。 El Hajal J等[4]还比较了质量流率、对比压力、管内径和工质物性对新流型图流型转换标准的影响。发现对于质量流率,由于Rouhani S Z等[24]的空隙率计算模型中需要设定一个设计质量流率值(Gset),其对除xI-A外的其他流型转换标准均存在一定的影响,El Hajal J等[4]提出该值最好取Gset=300 kg/(m2·s);而对比压力对GStrat的影响很小,对GWavy的影响在低干度范围较大,对xI-A的影响会随对比压力的增加而向高干度偏移,对GMist的影响则随对比压力的增加先增大后减小,且当工作压力接近工质的临界压力时,GMist值在全干度范围均很小;对于管内径,其对GStrat和xI-A没有影响,但对GWavy的影响会随管内径的减小在低干度范围获得较小值,对GMist的影响则随管内径的减小而变大;而工质物性对GStrat和GWavy仅在非常低的干度范围有较小的影响,对xI-A和GMist则存在较大的影响。图6所示为以工质为R134a,饱和温度为313.15 K和管内径为8 mm的工况为例的新流型图。 图6 El Hajal et al. (2003) 水平管内流动冷凝流型图Fig.6 El Hajal et al. (2003) map on condensation in horizontal tubes 上述提到的流型图均针对常规管径(D>3 mm),对于微管道,由于表面张力作用增强,流型及其转换标准与常规管道有明显的区别。Coleman J W等[25-27]进行了一系列R134a流动冷凝的流型实验,发现随着水力直径的减小,环状和间歇流的区域会增大,相对应的层状和波状流区域会减小,表明重力起主导作用的流型区域减小,表面张力作用强于重力作用。 2012年Kim S M等[28-29]对FC72进行了水平微管道(D=1 mm)内的流动冷凝实验,主要观察到的流型有泡状流、块状流(Slug)、块状流向环状流的过渡区(Transition,简写为T)和环状流,并将环状流细分为气液界面光滑的环状流(Smooth-Annular,简写为SA)和气液界面呈波纹状的环状流(Wavy-Annular,简写为WA)。Kim S M等[28-29]以Martinelli数(Xtt)和Soliman H M[30]提出的修正Weber数(We*)为横纵坐标,基于实验流型数据提出新的流型图,如图7所示。 (20) 其中, (21) (22) (23) 图7 Kim et al. (2012)水平微管道内流动冷凝流型图Fig.7 Kim et al. (2012) map on condensation in horizontal tubes 2014年Nema G等[31]利用R134a大范围工况(1 1)对于微管道(Bo≤Bocritical) (1)当WeG>700且Xtt<0.175时,为雾状流(M); (3)当WeG≥35或WeG<35且Xtt≤0.3521时,为环状流(A); (4)当6≤WeG<35且Xtt>0.3521时,为I-A转换线; (5)当WeG<6且Xtt>0.3521时,为间歇流(I)。 2)对于小管内径(Bo>Bocritical) (1)当WeG>700且Xtt<0.175时,为雾状流(M); (3)当WeG>6+7(Bo-Bocritical)1.5时,为环状流(A); (4)当JG≥2.75且WeG<6+7(Bo-Bocritical)1.5时,为半环状流(Semi-A); (5)当JG<2.75且{WeG>35或(WeG≤35且Xtt (6)当6 (7)当WeG<6且Xtt>Xtt,slug时,为间歇流(I)。 其中, (24) (25) Xtt,mod=Xtt-Xtt,slug (26) 当Bo≤Bocritical时: Xtt,slug=Xtt0=0.3521 当Bo>Bocritical时: (27) Xtt1=1.6-Xtt0=1.2479 本文针对水平管内流动冷凝流型图的研究进展进行了较为全面的分析与整理。研究结果显示,针对绝热条件及流动沸腾提出的两相流型图应用于流动冷凝两相流动状态的预测存在一定的偏差,目前大多数流动冷凝流型图均基于前者提出。现有的流型图大多针对常规管道,由于微管道与常规管道的流动冷凝机理不同,如管内径越小,流体表面张力对流动的影响越大,导致两者流型及其转换标准存在差异。尽管水平管内流动冷凝流型图的研究已有一定成果,但该领域尚有很多问题有待解决: 1)目前针对流动冷凝提出的流型图的还很少,特别是用于微管道的冷凝流型图尤为缺乏。 2)目前的流型图大多基于常温(实验饱和温度不低于0 ℃)常压(实验对比压力低于0.5)工质的实验流型数据提出的,其扩展应用于低温或高压等工质存在一定的困难。 3)许多研究者认为基于流型的传热及压降模型比经验模型更准确且应用更广,但目前较多的流型图研究与传热及压降模型研究分开,未能实现较好的联系。 符号说明 A——流道截面积,m2 ALd——流道液相无量纲截面积,m2 AGd——流道气相无量纲截面积,m2 Bo——Bond数 Bocritical——临界Bond数 D——管内径,m DL——液相截面直径,m Eo——Eötvos数 FE——Eötvos数的函数 Fr——Froude数 g——重力加速度,m/s2 G——质量流率,kg/(m2·s) GMist——间歇流/环状流与雾状流转换质量流率,kg/(m2·s) Gset——设计质量流率,kg/(m2·s) GStrat——层状流与波状流转换质量流率,kg/(m2·s) GWavy——波状流与间歇流/环状流转换质量流率,kg/(m2·s) GW——转换质量流率,kg/(m2·s) hLd——液相液面高度的无量纲数 JG——无量纲气相速度 Re——Reynolds数 Si——汽液相界面周长 Su——Suratman数 T——无量纲耗散转换系数 u——流速,m/s We——Weber数 We*——修正Weber数 x——干度 xI-A——间歇流与环状流转换干度 Xtt——Martinelli数 Xtt,mod——修正的Martinelli数 Xtt,slug——塞状流Martinelli数 α——空隙率 μ——粘性力,Pas ρ——密度,kg/m3 σ——表面张力,N/m ξ——因子 下标 G——气相 h——均相 L——液相 [1] Bell K J, Taborek J, Fenoglio F. Interpretation of horizontal in-tube condensation heat transfer correlations with a two-phase flow regime map[C] //Chem. Eng. Progr. Symp. Ser. Alhambra, Calif.: Heat Transfer Research, 1970: 150-163. [2] Kattan N, Thome J R, Favrat D. Flow boiling in horizontal tubes: part 3—development of a new heat transfer model based on flow pattern[J]. Journal of Heat Transfer, 1998, 120(1): 156-165. [3] Wojtan L, Ursenbacher T, Thome J R. Investigation of flow boiling in horizontal tubes: part II—development of a new heat transfer model for stratified-wavy, dryout and mist flow regimes[J]. International Journal of Heat & Mass Transfer, 2005, 48(14): 2970-2985. [4] El Hajal J, Thome J R, Cavallini A. Condensation in horizontal tubes, part 1: two-phase flow pattern map[J]. International Journal of Heat and Mass Transfer, 2003, 46(18): 3349-3363. [5] Thome J R, El Hajal J, Cavallini A. Condensation in horizontal tubes, part 2: new heat transfer model based on flow regimes[J]. International Journal of Heat and Mass Transfer, 2003, 46(18): 3365-3387. [6] Quibén J M. Experimental and analytical study of two-phase pressure drops during evaporation in horizontal tubes[D]. Lausanne, Switzerland: Swiss Federal Institute of Technology, 2005. [7] Quibén J M, Thome J R. Flow pattern based two-phase frictional pressure drop model for horizontal tubes. part I: diabatic and adiabatic experimental study[J]. International Journal of Heat & Fluid Flow, 2007, 28(5): 1049-1059.[8] Quibén J M, Thome J R. Flow pattern based two-phase frictional pressure drop model for horizontal tubes, part II: new phenomenological model[J]. International Journal of Heat and Fluid Flow, 2007, 28(5): 1060-1072. [9] Cheng L, Ribatski G, Thome J R. Two-phase flow patterns and flow-pattern maps: fundamentals and applications[J]. Applied Mechanics Reviews, 2008, 61(5): 1239-1249. [10] Palen J W, Breber G, Taborek J. Prediction of flow regimes in horizontal tube-side condensation[J]. Heat Transfer Engineering, 2007(1): 47-57. [11] Baker O. Simultaneous flow of oil and gas[J]. The Oil and Gas Journal, 1954, 53: 185-190. [12] Mandhane J M, Gregory G A, Aziz K. A flow pattern map for gas—liquid flow in horizontal pipes[J]. International Journal of Multiphase Flow, 1974, 1(4): 537-553. [13] Taitel Y, Dukler A E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow[J]. AIChE Journal, 1976, 22(1): 47-55. [14] Breber G, Palen J W, Taborek J, et al. Prediction of horizontal tube side condensation of pure components using flow regime criteria[J]. Journal of Heat Transfer, 1980, 102(3): 471-476. [15] Soliman H M. Analytical and experimental studies of flow patterns during condensation inside horizontal tubes[D]. Manhattan, USA: Kansas State University, 1974. [16] Tandon T N, Varma H K, Gupta C P. A new flow regimes map for condensation inside horizontal tubes[J]. Journal of Heat Transfer, 1982, 104(4): 763-768. [17] Soliman H M, Azer N Z. Visual studies of flow patterns during condensation inside horizontal tubes[C] //Proceedings of the Fifth International Conference. Tokyo, Japan: Society of Heat Transfer of Japan, 1974: 241-245. [18] Cavallini A, Censi G, Del Col D, et al. Condensation of halogenated refrigerants inside smooth tubes[J]. HVAC&R Research, 2002, 8(8): 429-451. [19] Rabas T J, Arman B. The effect of the exit condition on the performance of in-tube condensers[J]. Heat Transfer Engineering, 1995, 21(1): 4-14. [20] Cavallini A, Col D D, Doretti L, et al. Condensation in horizontal smooth tubes: a new heat transfer model for heat exchanger design[J]. Heat Transfer Engineering, 2006, 27(8): 31-38. [21] Kattan N, Thome J R, Favrat D. Flow boiling in horizontal tubes: part 1—development of a diabatic two-phase flow pattern map[J]. Journal of Heat Transfer, 1998, 120(1): 140-147. [22] Zürcher O, Thome J R, Favrat D. Evaporation of ammonia in a smooth horizontal tube: heat transfer measurements and predictions[J]. Journal of Heat Transfer, 1999, 121(1): 89-101. [23] Thome J R, Hajal J E. Two-phase flow pattern map for evaporation in horizontal tubes: latest version[J]. Heat Transfer Engineering, 2003, 24(6): 3-10. [24] Rouhani S Z, Axelsson E. Calculation of void volume fraction in the subcooled and quality boiling regions[J]. International Journal of Heat and Mass Transfer, 1970, 13(2), 383-393. [25] Coleman J W, Garimella S. Two-phase flow regime transitions in microchannel tubes: the effect of hydraulic diameter[J]. ASME-Publications-HTD, 2000, 366: 71-84. [26] Coleman J W, Garimella S. Visualization of refrigerant two-phase flow during condensation[C]//34th National Heat Transfer Conference. Pittsburgh, USA, 2000.[27] Coleman J W, Garimella S. Two-phase flow regimes in round, square and rectangular tubes during condensation of refrigerant R134a[J]. International Journal of Refrigeration, 2003, 26(1): 117-128. [28] Kim S M, Kim J, Mudawar I. Flow condensation in parallel micro-channels-part 1: experimental results and assessment of pressure drop correlations[J]. International Journal of Heat & Mass Transfer, 2012, 55(4): 971-983. [29] Kim S M, Mudawar I. Flow condensation in parallel micro-channels-part 2: heat transfer results and correlation technique[J]. International Journal of Heat & Mass Transfer, 2012, 55(4): 984-994. [30] Soliman H M. The mist-annular transition during condensation and its influence on the heat transfer mechanism[J]. International Journal of Multiphase Flow, 1986, 12(2): 277-288. [31] Nema G, Garimella S, Fronk B M. Flow regime transitions during condensation in microchannels[J]. International Journal of Refrigeration, 2014, 40(3): 227-240. About the corresponding author Gong Maoqiong, male, professor, Key Laboratory of Cryogenics, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, +86 10-82543728, E-mail: gongmq@mail.ipc.ac.cn. Research fields: cryogenic technology. A Review on Flow Pattern Maps of Condensation in Horizontal Tubes Zhuang Xiaoru1, 2Gong Maoqiong1Zou Xin1Chen Gaofei1Wu Jianfeng1 (1. Key Laboratory of Cryogenics, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing, 100190, China; 2. University of Chinese Academy of Sciences, Beijing, 100049, China) Two-phase flow pattern is important for investigating heat transfer coefficients and pressure drops of condensation in horizontal tubes. And the flow pattern maps are the usual approach to predict flow regimes and their transitions. In this paper, a review on flow pattern maps and flow regime transitions of condensation in horizontal tubes of Breber et al. (1980), Tandon et al. (1982), Cavallini et al. (2002, 2006), El Hajal et al. (2003), Kim et al. (2012) and Nema et al. (2014) is presented. In recent researches, most two-phase flow pattern maps have been developed for the adiabatic and evaporation conditions. The applications of those maps on the condensation are not applicable and the flow pattern maps of condensation are still lacks. Moreover, this paper presents that a large number of the recent flow pattern maps have been conducted with macroscale channels and conventional reduced pressure and temperature refrigerants. Those maps could not apply to microscale channels and high pressure and low temperature refrigerants. At last, the majority of recent work didn't well combine the flow regime with the investigation of heat transfer coefficient and pressure drop. flow condensation; flow pattern; flow pattern map; horizontal tube 0253- 4339(2016) 02- 0009- 08 10.3969/j.issn.0253- 4339.2016.02.009 国家自然科学基金(51322605)和国家科技重大专项(2011ZX05039-001-004)资助项目。 (The project was supported by the National Natural Science Foundation of China (No. 51322605) and National Science and Technology Major Project (No. 2011ZX05039-001-004).) 2015年5月14日 TK124; TQ021.3; TQ051.5 A 简介 公茂琼,男,研究员,中国科学院理化技术研究所低温工程重点实验室,(010)82543728,E-mail:gongmq@mail.ipc.ac.cn。研究方向:低温制冷技术。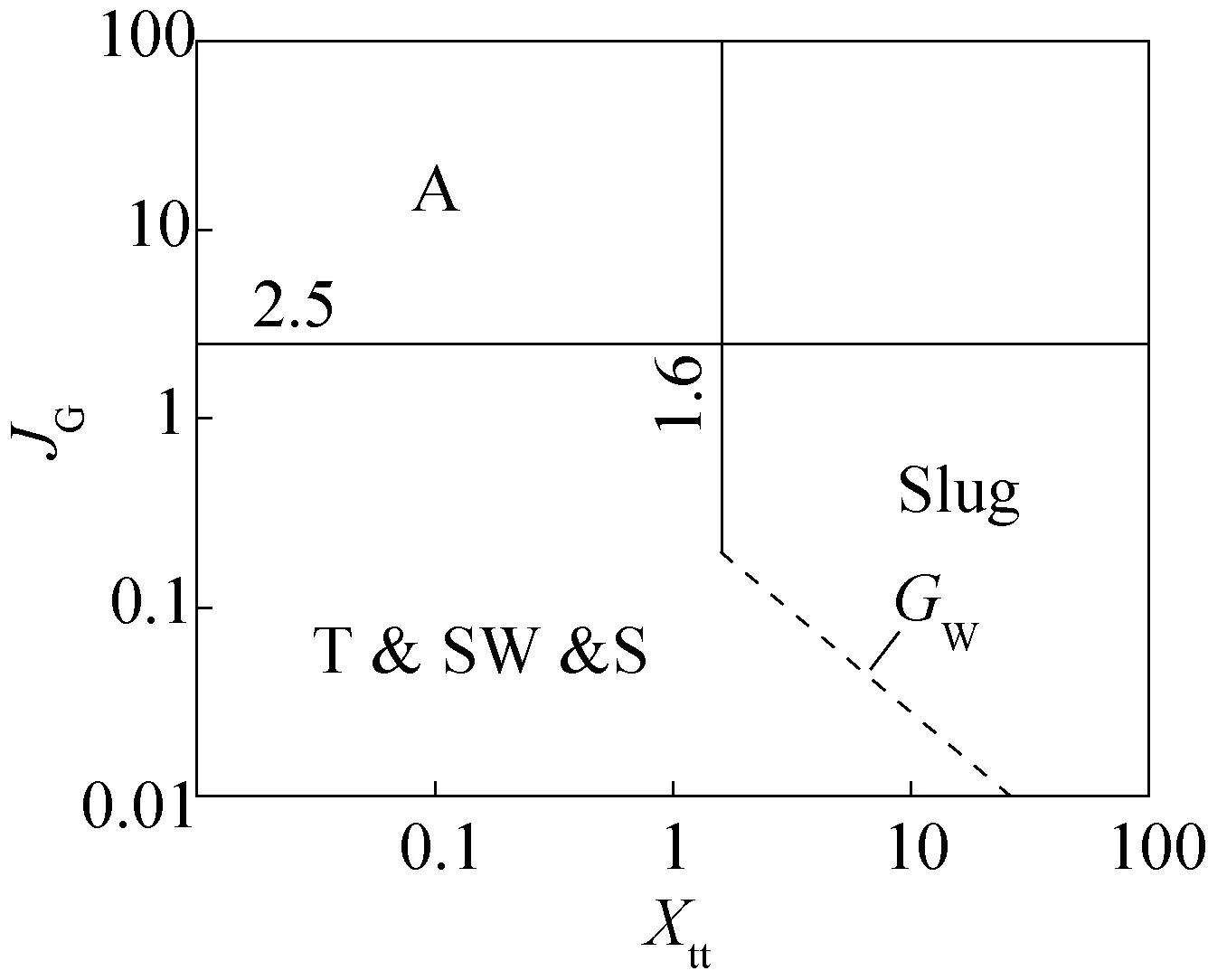
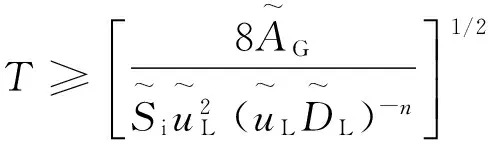
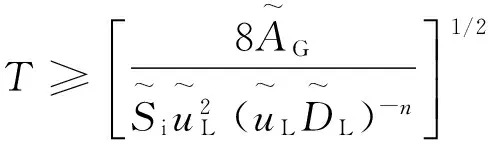
3 结论


