从解题走向研究题——以一道竞赛题为例谈解题教学

白金强

（河北省高碑店市教师发展中心）

美国数学家哈尔莫斯指出：数学真正的组成部分是问题和解，解题才是数学的心脏.解题既是教学的手段又是教学的目的.解题教学的目的并不单纯是为了求得问题的结果，真正的目的是为了提升学生的数学素养，而数学素养的提高要从研究题开始.

一、问题呈现

题目（选自2017年全国初中数学联合竞赛）如图1，设O是四边形ABCD的对角线AC，BD的交点，若∠BAD+∠ACB=180°，BC=3，AD=4，AC=5，AB=6，则的值为（ ）.

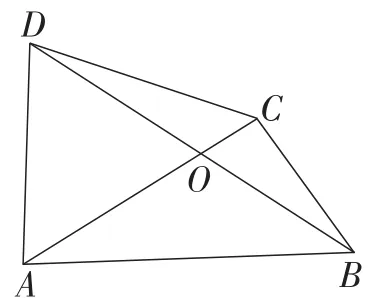
图1

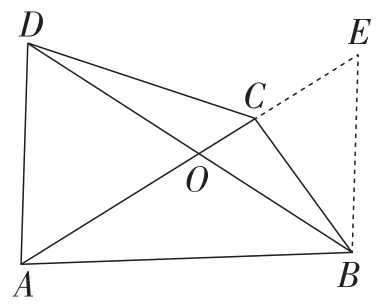
图2

解法1：如图2，过点B作BE∥AD，交AC的延长线于点E，

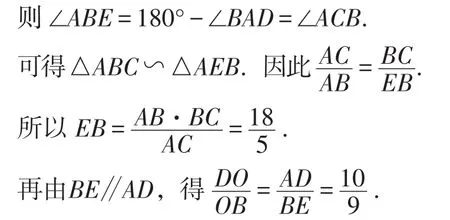
单从解题的角度看这道题，学生只要快速、准确选出正确答案即可.从心理学角度分析，解题只是每个人的个体行为，而对解题教学来说，教学的价值更大.因此，在日常教学中，教师应有设问意识和应用意识，通过设问来引发学生的深度思考，学会以研究的视角审视解题.

二、问题思考

1.理清条件，明确解题思路

（1）理解题意.

题目中的已知条件有哪些？结论是什么？

条件：∠BAD+∠ACB=180°，BC=3，AD=4，AC=5，AB=6；

（2）思路探求.

此题的关键条件是∠BAD+∠ACB=180°，如何围绕这个条件寻找解题思路呢？解法1是通过作平行线巧妙地构造出了∠BAD的补角∠ABE，再设法证明△ABE∽△ACB来求解.

思路1：①构造∠BAD的补角；②作与有关的平行线；③构造和△ABC相似的三角形；

思路3：解法迁移，变式拓展.

三、问题解决

思路1：借助平行（线），巧构（补）角

围绕此题的关键条件∠BAD+∠ACB=180°和所求结果，展开思路.

设问1：由联想到学过的知识是什么？

同旁内角互补，两直线平行.两直线平行，可以得出对应线段之间的比，遗憾的是互补的两个角不能直接推导出平行线.

设问2：怎么才会有这个比值呢？

显然通过构造平行线可以实现，有几种方法呢？

解法2：如图3，过点B作BN∥AC，交DA的延长线于点N，

图3

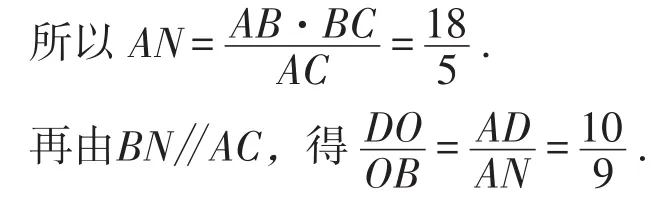
还可以怎样作辅助线呢？

解法3：如图4，过点D作DP∥AC，交BA的延长线于点P，

则∠DAB的邻补角∠DAP与∠BCA相等，且∠P=∠CAB.

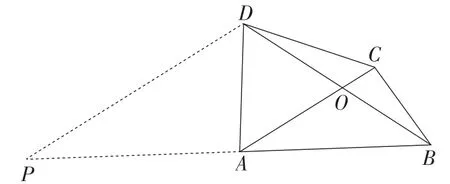
图4

解法4：如图5，过点D作DQ∥AB，交AC的延长线于点Q，

则∠DAB的补角∠ADQ与∠BCA相等，且 ∠Q=∠CAB.

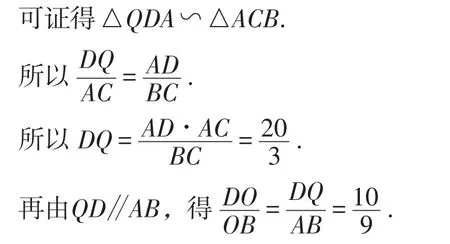
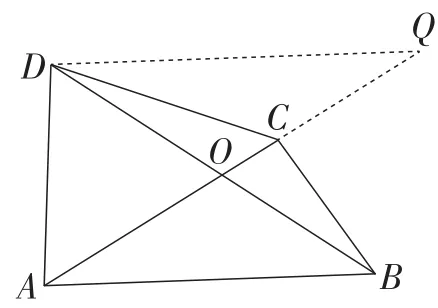
图5

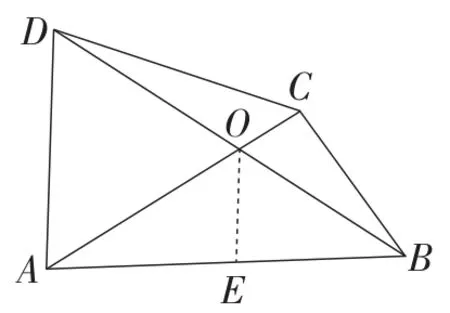
图6

解法5：如图6，过点O作OE∥AD，交AB于点E，

由∠BAD+∠ACB=180°，

容易证明∠OEA=∠ACB.

所以△OEA∽△ACB.

思路2：基于确定性，巧用面积法

设问3：与有关的三角形有哪些？

有△AOD和△AOB，△COD和△COB，△ADC和△ABC.

设问4：分析关于△ABC的已知条件，发现了什么？

发现△ABC三条边的长度是已知的，则三角形的面积是确定的，可以求出高.所以，围绕△ADC和△ABC的面积比来思考解题的方法，则是另一种不同的思路.

解法6：如图7，过点C作CG⊥AB，过点B作BE⊥AC，交AC的延长线于点E，过点D作DF⊥AC.

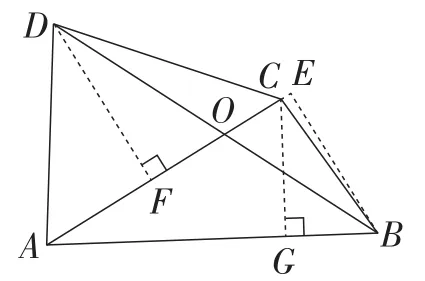
图7

由已知 ∠BAD+∠ACB=180°，而 ∠CAB+∠CBA+∠ACB=180°.

所以∠DAB=∠CAB+∠CBA，即∠DAC=∠ABC.

在△ACB和△ADC中，有BC=3，AC=5，AB=6，AD=4，

则CG=3sin∠ABC，DF=4sin∠DAC.

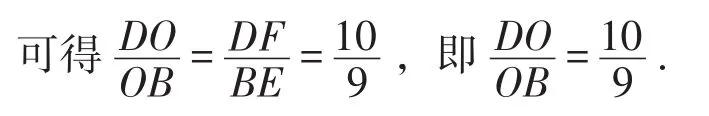
解法6的关键处在于利用∠BAD+∠ACB=180°发现了隐含条件∠DAC=∠ABC，然后利用三角函数知识求出高的表达式，通过面积比的变换完成求解.这种方法和解法1～解法5的思考角度不同，所用到的知识也不同.

思路3：解法迁移，变式拓展

前面六种解法都是基于“比例的基本性质”这一本质属性展开.解法1～解法5立足于平行线段成比例，解法6则立足于通过面积比的变换来求解.教师如何带领学生从日常教条式的“做出来”或“做对”走向不断思考和深化问题，理清问题在具体情境中的复杂变化，洞悉问题本质，大胆对解法迁移、变式拓展，对积累丰富的解题经验大有裨益.

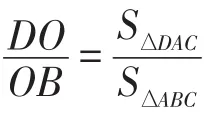
如果从研究题的视角看待这一结论，首先想到的是减弱原题中的条件，看看结论会发生哪些变化.

如若去掉原题中的“若∠BAD+∠ACB=180°，BC=3，AD=4，AC=5，AB=6”，则结论会发生哪些变化？

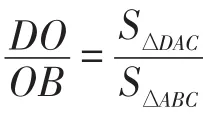
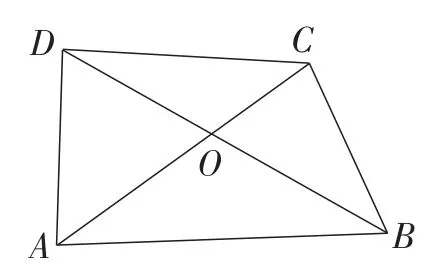
图8

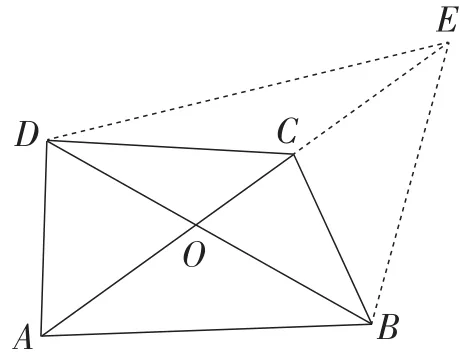
图9

证明：（方法1）如图9，延长AO至点E，使OE=AC，连接DE，BE，

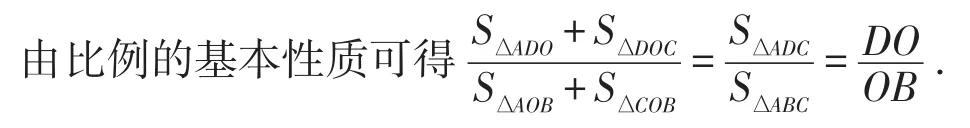
问题得证.

变式1：如图10，设点O是四边形ABCD的对角线AC，BD的交点，若∠ADC=∠CAB，AB=3，AC=4，DC=5，AD=6. 求的值.

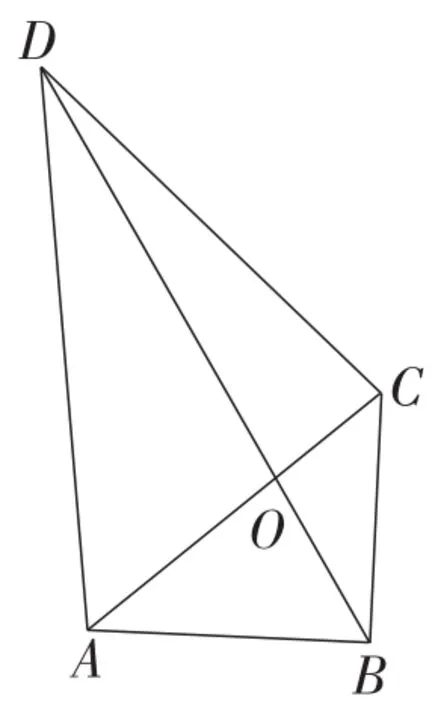
图10

变式2：如图11，设点O是四边形ADBC的对角线AB，CD的交点，若∠ACB=∠ABD，BD=3，AB=4，AC=5，BC=6，求的值.

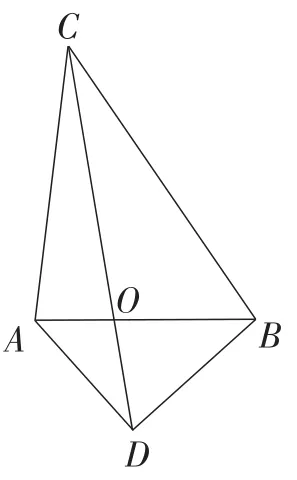
图11

变式1和变式2是对解法6中用到的隐含条件∠DAC=∠ABC的迁移.那么，直接给出∠ADC=∠CAB和∠ACB=∠ABD，还可以进一步变化吗？读者可以自己尝试.

四、结束语

通过对一道竞赛题的分析，可以给我们如下启示：第一，准确发现题目中的隐含条件和其中的关联，可以获得解题思路.第二，解题教学不能仅仅满足于解出答案，还要思考多种解法.教师既要引导学生会按照一种解法平行思考（解法2～解法5），又要启发学生从多角度思考（解法6）.第三，养成变式拓展研究问题的习惯，通过变式研究可以深化问题，洞悉问题的本质.教学中只有做到多层次、多角度、全方位地发现问题、提出问题和研究问题，才能不断地获得新的发现，积累新的解题经验，从而全面提升学生的数学素养.