在画图和构图中破解问题——品2018年天津市中考试卷第25题有感

刘家良

（天津市静海区沿庄镇中学）

“数”与“形”做为数学殿堂中的两大支柱，随着知识的纵深发展，两者之间的互补性就表现得越强，以至于成为一个不可分割的整体.特别是在题目没有给出相应图形的情况下，解题者若能根据文字表述画出相应的图形，再结合以往的经验，在联想中进行构图，就会使问题中隐含的数量关系渐渐突显，随之产生破解问题的思路和方法.细品2018年天津市中考试卷第25题，深感画图和构图环节对解题思维所产生的辅助和建构作用.基于此，笔者就养成学生“以形助数”的意识和习惯谈些拙见.

一、试题解析

题目（2018年天津卷）在平面直角坐标系中，点O(0，0)，点 A (1，0).已知抛物线y=x2+mx-2m（m是常数），顶点为点P.

（1）当抛物线经过点A时，求顶点P的坐标；

（2）若点P在x轴下方，当∠AOP=45°时，求抛物线的解析式；

（3）无论m取何值，该抛物线都经过定点H.当∠AHP=45°时，求抛物线的解析式.

分析：对于第（1）小题，先用待定系数法求二次函数的解析式，再利用抛物线的顶点坐标公式求得顶点坐标.

对于第（2）小题，只有文字表述而缺乏相应图形的匹配，需要先结合题意画出草图.由∠AOP=45°可知顶点P位于第四象限的角平分线上，点P的这一特殊位置表明点P的横、纵坐标互为相反数，从而列出方程.

对于第（3）小题，先通过观察或利用关于x的方程ax=b（x为未知数）的解的某些结论得到定点H的坐标，这需要对“无论m取何值，该抛物线都经过定点H”进行理解和破译.此题没有给出相应图形，由∠AHP=45°可以画出符合条件的两条射线HP.如何求得射线HP所在直线的解析式是问题思考的出发点.由45°角联想到构造等腰直角三角形，使45°角既有图形的“归属感”，又能得到射线HP上的点D，这一想法是确定直线HP的需要，是源自第（2）小题的类比.

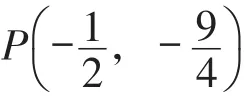
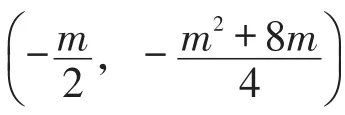
由题意知，射线OP是第四象限的角平分线，

解得m1=0或m2=-10.

当m=0时，点P与点O重合，而点P在x轴下方，

所以m=0应舍去.

所以m=-10.

所以y=x2-10x+20.

（3）（方法1）由y=x2+mx-2m=(x-2)m+x2知，

当x=2时，无论m取任何实数，而对应的y值都等于4.得点H的坐标为H(2，4).

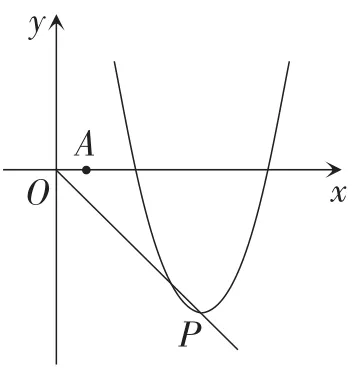
图1

情况1：如图2，当点P在AH的左侧时，过点A作DA⊥AH，交射线HP于点D，过点D作DE⊥Ox于点E，过点H作HG⊥Ox于点G.

因为∠DAH=90°，∠AHP=45°，

所以AH=AD.

易证得∠DAE=∠AHG.

由此可得△ADE≌△HAG.

所以DE=AG=1，AE=HG=4，OE=AE-OA=3.

得点D的坐标为D(-3，1).

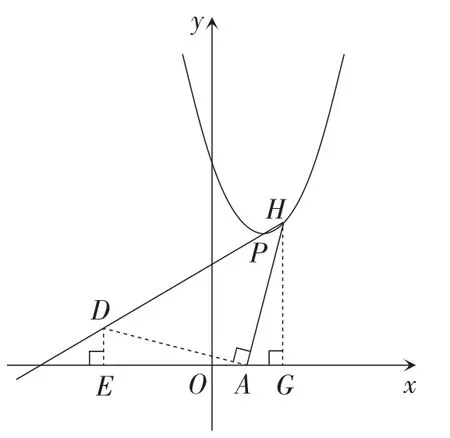
图2

情况2：如图3，当点P在AH的右侧时，求得点D的坐标为D(5，-1)，直线DH的解析式为.

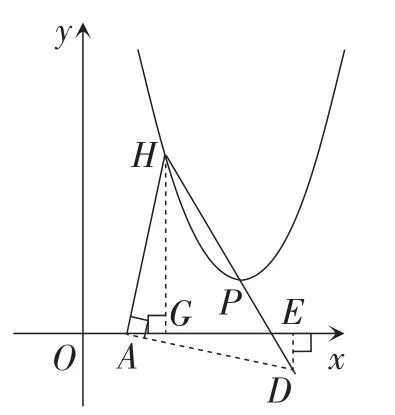
图3

（方法2）如图4和图5，分别过点A作AQ⊥HP于点Q.

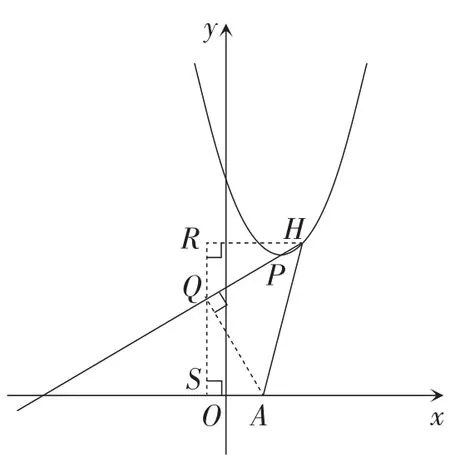
图4

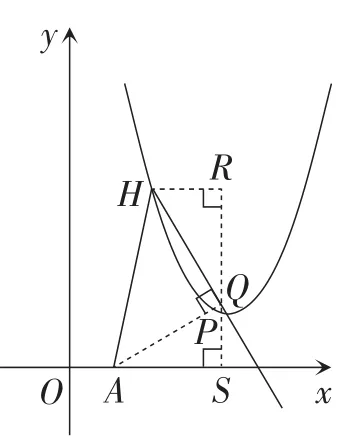
图5

因为∠AHP=45°，所以AQ=QH.

过点Q作QS⊥Ox于点S，过点H作x轴的平行线，交直线SQ于点R，则∠R=90°.

易证得△HRQ≌△QSA.

得HR=QS，QR=AS.

以下同方法1，略.

【评析】解第（3）小题除需要画图象外，还有几何图形特征及其性质的参与.此题需要根据题意画出图形，而图形中蕴含的条件信息不能解决问题，需要深挖45°角“背后”隐藏的信息，此时可以通过构图和拓展图形来解决问题.受“半角模型”的启发，萌发作垂直构造等腰直角三角形的念头，由此激活边、角之间的相互联系，从而找到解题的切入点.该问题解决的两种思路都是构造“一线三垂直”模型，通过构图使问题求解的条件变得充足、清晰.

二、养成“以形助数”的思维意识

通过对上述中考试题的解析，我们体验到图形对解题思维的建构所发挥的辅助及催化作用.几何图形承载了图形元素之间的因果联系.借助画图、构图解决问题是衡量数学能力高低的一块试金石.而有的学生还滞留在“数”的圈子里，往往认为画图麻烦、浪费时间.学生因有这种不愿画图的心理，影响了数形结合与转化思想的应用，缺失了解决问题的一种重要手段.那么，如何让学生产生“以形助数”的想法呢？

1.文图交融

多数学生习惯于将图形中承载的因果信息用文字或符号展现出来，而根据文字描述画出相应的图形是其薄弱之处.改善这一现状，需要将图形的定义及相关定理的文字、图形、符号三种语言的表述交织在一起，通过将文字图形化，让学生感受图形为问题解决带来的直观效果，逐步使学生养成见文字想图形的思维习惯.

2.寻找基本图形

在解题过程中，可以将给定的图形与基本图形相对比，在图形的联想、分解中找到基本图形的影子，撬开问题解决的支点，为几何图形的解答提供思维路径.

例1（选自人教版《义务教育教科书·数学》八年级上册第56页第9题）如图6，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为点D，E，AD=2.5cm，DE=1.7cm.求BE的长.

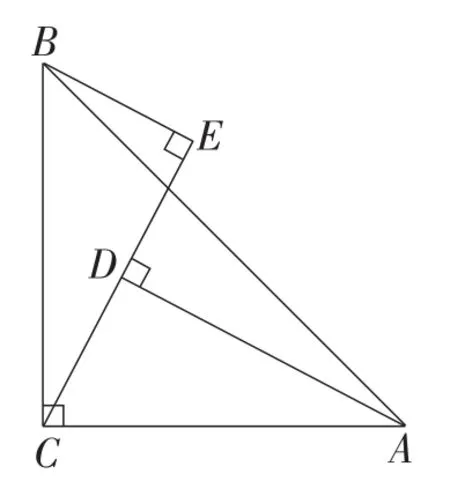
图6

解：由同角的余角相等，可得∠ACD=∠CBE.再结合AC=BC，可得△ACD≌△CBE.于是BE=CD，CE=AD.而CD=CE-DE，至此问题求解就有了眉目.

【评析】图6中的直线CE上有三个垂足点，隐藏着“一线三垂直”模型.若学生能看出这个模型，则能迅速寻找到图中的全等三角形，从而找到解决问题的入口.

3.拓展基本图形

将教材中某些定理的结论适时向纵深引入，在挖掘中发现图形中蕴含的其他结论，这对学生的联想思维、知识之间的沟通和脉络的形成都是大有益处的.例如，关于切线长定理，在人教版教材中给出如下内容：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.教师若能结合学生的基础状况和思维现状，适时引导，则会衍生出许多结论.例如，从圆外一点引圆的两条切线，则圆心和圆外一点的连线垂直平分两切点的弦；圆心和圆外一点的连线同圆弧的交点是圆外一点和两切点组成的三角形的内心；圆心、圆外一点和两切点组成的四边形有且仅有一个外接圆，等等.

4.构造基本图形

由图形的条件特征引发联想，通过添加辅助线，将图形的局部还原成一个基本图形，从而开启解题思路.

例2如图7，在△ABC中，M是BC的中点，AP是∠ABC的平分线，BP⊥AP于点P，AB=6，AC=8.求PM的长.

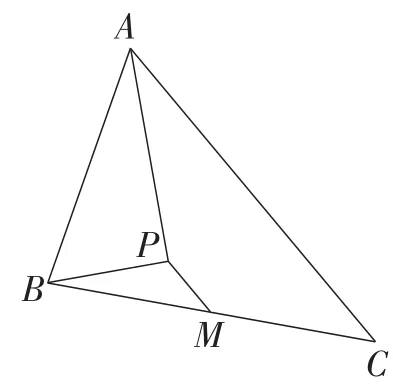
图7

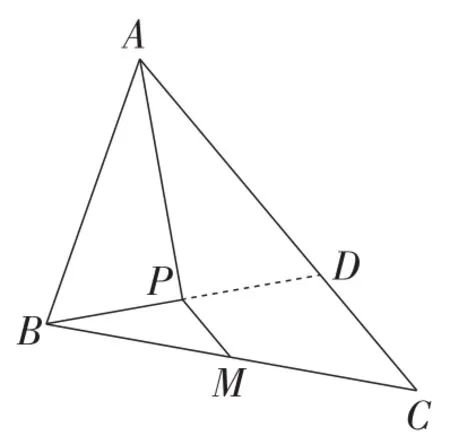
图8

解：由AP是∠BAC的平分线，BP⊥AP于点P，联想到等腰三角形“三线合一”性质，延长BP，交AC于点D，如图8所示.由此可以证得△APD≌△APB.因此AD=AB=6，PD=BP.又因为BM=CM，所以

【评析】此题基于“角平分线+垂线⇒等腰三角形”模型，将图形局部还原为一个基本图形.

例3如图9，在△ABC中，∠ACB=90°，AC=4，BC=2，以AB为边向外作等腰直角三角形ABD，则CD的长是_____.

分析：此题需分三种情况考虑，而这三种情况都是在△ABD的直角顶点处构造“一线三垂直”模型，如图10所示.

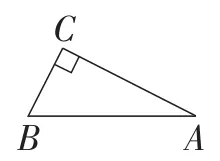
图9

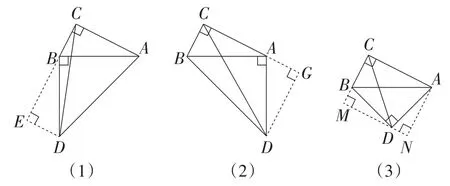
图10

解：（1）当点B为直角顶点时，过点D作DE⊥BC，交CB的延长线于点E，如图10（1）所示；

（2）当点A为直角顶点时，过点D作DG⊥CA，交CA的延长线于点G，如图10（2）所示；

（3）当点D为直角顶点时，过点D作DM⊥CB，交CB的延长线于点M，过点A作AN⊥DM，交MD的延长线于点N，如图10（3）所示.

由图10（1）至图10（3），依次求得CD的长为

【评析】例1是识别“一线三垂直”模型，例3需要构造该模型.学生若经历识别、构造这种思维生长的历练，久而久之就会感受、体验到图形的魅力，从内心产生一种对构造图形辅助线的需求.

三、结束语

画图、构图要植根于图形的定义、定理的教学过程中，需要教师的示范和学生的及时跟进与领悟.通过文字与图形的交融、碰撞，使学生认识到图形的重要性.通过图形的局部识别，让图形中隐含的意义植根于学生心间；通过图形的构造，提升学生由此及彼的联想能力.画图、构图作为解决数学问题的一种内在需要，蕴涵了数形结合与转化思想，而这种思想一旦融入于学生的意识之中，就会为学生搭建由知识通向能力的桥梁.