强调反思解释 优化学习品质
胡素芬
(上海市航头学校)
复习是课堂教学的重要阶段,尤其对数学复习课来说,深入理解知识,提炼数学思想,优化解题策略,提高综合能力具有关键作用.但是复习课的教学设计又因为各种原因,要么定位模糊,要么组织不当,要么方法单一,要么针对性不强,甚至有固定套路:概念、定理回忆、例题精讲、练习、测试反馈,这样的课堂会让学生感到枯燥无味,从而影响复习效率.
数学学习的过程是学生独立思考的过程,是学生反复练习的过程,是学生领悟思想的过程.而这一切都建立在学生良好的数学学习品质的基础上.在开展数学学科核心素养的研究过程中,我们主要就好奇与兴趣、专注与坚持、想象与创造、反思与解释等品质入手对各种课型进行教学设计(如图1).如果说好奇与兴趣、专注与坚持、想象与创造能够在新授课上大放光彩,那么在复习课的设计中就需要更加重视学生反思与解释的教学过程.接下来以2018年湖南省长沙市中考试卷的第25题为载体,谈一谈在复习课的课堂设计中如何引导学生关注反思与解释.

图1
一、试题呈现
题目(2018年湖南·长沙卷)如图2,在平面直角坐标系xOy中,函数(m为常数,m>1,x>0)的图象经过点P(m,1)和点Q(1,m),直线PQ与x轴、y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为点A,B.

图2
(1)求∠OCD的度数;
(2)当m=3,1<x<3时,存在点M使得△OPM∽△OCP,求此时点M的坐标;
(3)当m=5时,矩形OAMB与△OPQ的重叠部分的面积能否等于4.1?试说明理由.
二、一题多解
此题的第(1)小题证明OC=OD即可以解决问题,略,第(3)小题分三部分进行分类讨论,本文重点研究第(2)小题.





三、反思交流,优化学习品质
针对复习课效率不高的现状,许多教师已经意识到通过精心设计教学来提高课堂教学效率,于是一题多解、一题多变和一法多用的复习课三步曲奏响了复习课的主旋律.如果说一题多解促使学生的想象和创造,一题多变引发学生的好奇与兴趣,一法多用训练学生的专注与坚持,那么如何引导学生进行反思检验,对已经得到的答案进行合理解释,从而进一步优化学习品质就更加值得我们深思和研究.
1.反思促进概念理解
复习课的解题教学过程中,教师要引导学生积极反思为什么有的解法需要检验,有的解法不需要,为什么各种解法的检验方法又各不相同?事实上对解题结果的反思就是对解题方法的反思,而对解题方法的反思归根结底就是对数学概念的反思.
数学概念一般是以准确而精炼的数学语言运用定义的形式给出的,具有高度的抽象性、严密的精确性和广泛的应用性,是学生进行数学思维的核心.由于课时安排和学情限制,概念形成多数是孤立的、绝对的.也就是说尽管数学概念无法一次成型,但是日常教学中还是存在大量以“计算”代替“推理”的现象.
以题目的解法1为例,很多学生在中考考场上能够根据第(2)小题中的条件△OPM∽△OCP直接列出等式,但是其中很多人没有求出点M的坐标,还有部分学生求出a的值没有带入检验并舍去.针对这一现象,教师需要在方程和方程组的概念教学时多问学生几个为什么,提出反思性学习提纲:(1)研究的条件是什么?(2)研究的对象是什么?(3)方程和方程组的区别和联系是什么?(4)解方程组的实质是什么?经过反思深化学生对初中数学教材中方程和方程组的理解,并在头脑中对解方程组形成较完整的流程,深化学生对方程组的知识建构.
对于概念,要全面、准确理解其内涵和外延,才能达到理解、掌握、灵活应用的目的.学习数学不能仅仅停留在“知其然”的层面上,更重要的是还能“知其所以然”.所以,教师不仅要引导学生对解题结果进行检验,还要培养学生熟练选择恰当的检验方法,促使学生理解检验的必要性和合理性.教师重视引导学生对类似的概念之间不同结构与本质区别的反思,使学生深刻地理解相关概念形成的背景、条件、过程、作用和延续.通过反思此题中检验方程的解的合理性,对于增根的成因分析,如何正确对待方程根的检验问题等都能优化学生的学习品质.
2.反思完善解题策略
数学家波利亚在《怎样解题》中对数学解题划分为四个阶段:弄清问题—拟定计划—实现计划—回顾,其中“回顾”就是解题后的反思,它是对解题思维过程的深化和提高.解题过程的反思,实际是解题学习的信息反馈调控阶段,通过反思,有利于学生深层次的建构.
在反思环节中,学生不难发现各种解题方法的切入点虽然不同,但是后一阶段基本都是通过方程求解点M的横坐标,而对于解出的不同答案除了最后一种解法外,其他解法都存在一个检验根的合理性的环节.为什么这道题目的解答方法都离不开检验呢?
反思各种解法,我们发现解法2和解法3中对点M横坐标的检验,是由于点M在反比例函数中第一象限的位置约束下所决定的必须舍负取正,解法4和解法5都是让学生思考为什么可用交轨法求点M的坐标,理由在于点M按题设要求应在45°角的一边上,在区间范围内直线与双曲线只有一个交点.解法6中让学生反思“扶正拉平”的添加辅助线构造“一线三等角”的常见模型的方法,而解法6列出的是一元一次方程,只有一个根,无需检验.那么解法1的检验方式为什么和其他解法的检验形式不一样?为什么需要检验?又应该如何解释呢?
根据△OPM∽△OCP,得到一组等式,而这组等式的实质是一个方程组为了简化计算过程,降低计算难度,解法1中先选择方程①进行变形,得到OP2=OC∙OM.然后将用a表示的线段带入得到方程.那么求解出a的值应该是方程①的解,并不一定是方程组的解,想要成为方程组的解还必须要满足方程②.所以解法1的检验环节与其说是检验不如说是继续解方程组更为恰当.也就是说,从方程组弱化成方程①的过程中,解的范围扩大了,通过方程②的检验才能得到原方程组的解.
通常情况下的方程组是按照如图9所示的流程解答,而这道题目的解法1为优化算法选用图10的流程来解答,检验就显得至关重要、不可或缺.
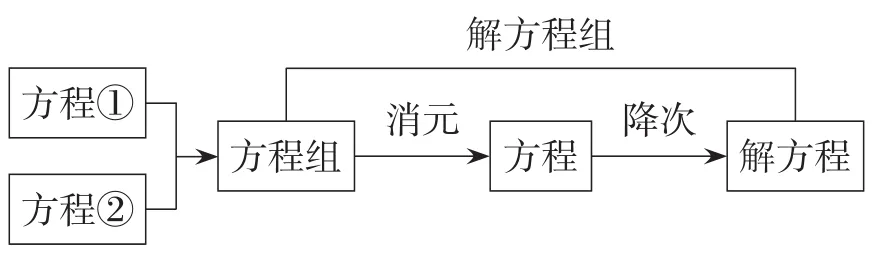
图9

图10
反思过程中,学生通过列出每一种解法的思维流程图,清楚每一种解法的数学本质,明确每一种解法的解题要点等措施,引导学生对整体解法进行反思.这样做有利于学生把握解题的整体思想,能够避免解法一开始就进入“死胡同”的境地,从而避免出现“不识庐山真面目”的现象,或者“只见树木,不见森林”等常见错误.
3.反思落实核心素养
注重反思和解释就是注重引导学生发现问题、提出问题、分析问题与解决问题.在基于数学核心素养的教学中,这应当是教师关注的重点.学生面对解题的多种方法,在教师引导下进行现象观察、提出问题、表达交流等,不仅经历了数学概念的形成过程,数学规律的发现过程,以及数学问题的解决过程,而且积累了数学活动经验,感悟到数学思想方法,切实体验严谨求实的科学态度和探究真理的科学精神.

甚至于在课堂上有一名学生当场总结出了“退倍进半”的结论,他说:“作PO的中垂线NF并连接PF,∠PFH=2∠POF,不就是向后退一步得到已知角的两倍吗?还可以反过来看这个图,即点O也可以看成以点F为圆心的圆与HF的延长线的交点,这不就是向前走一步就得到一半的已知角吗?”在这个过程中,这名学生至少经历了两次抽象,第一次是从具体问题情境抽象出具有两倍已知角的几何图形的过程,第二次是将辅助线和原三角形中的相关线段进行换位思考,抽象出一半已知角的几何图形.这两次抽象的过程不仅充分展现了直观想象,而且体现了数学思维的互逆性和多向性.
通过对解法3的反思,就能够在规律小结中培养学生的直观素养,在方法研究中提升学生的转化能力,在抽象归纳中强化学生的模型意识,另外明确由位置关系变化产生数量关系变化的过程和解方程的过程都在培养学生的运算素养,润物细无声地优化学生的学习品质.
古代思想家荀子在《劝学》中曰:“君子博学而日参省乎己,则知明而行无过矣.”学习中的反思如同生物体消化食物和吸收养分一样重要.学生的反思性学习与教师反思性教学相统一.它是学习中不可缺少的重要环节.反思与解释是数学学习心理品质的一项重要研究内容.反思性学习不但能维持学生学习活动的正常进行,更能强化学生学习的动力,增强学生克服学习困难的毅力,使学习到的知识内化,也是构建师生互动机制及学生的学习新方式.学会反思和解释是数学学科核心素养的需要,也是培养学生学习习惯的良方,更是优化学生学习品质的重要方面.

