费马点模型的前世今生

黄祥唇

（福建省德化县第六中学）

几何最值是中考热门的模型考点之一，它种类多，形式多样.三角形费马点问题，正是这类问题中的一个.图形的旋转变换是解决“费马点问题”非常重要的一种工具，用“图形的旋转变换”的主要目的就是要改变线段的位置，优化图形的结构，将不规则图形变为规则图形，或将分散的条件集中在一起，以便挖掘隐含条件，起到“画龙点睛”的作用，从而达到解决问题的效果.教师讲解一个问题时，尽量弄清楚问题的来龙去脉，才能让学生“解一题，会一类，通一片”.

一、前世

费马点是一个很神奇的点，也是一个很有用的点，更是一个有趣的数学问题，非常值得我们关注，并深入地研究.为了能更好地理解与运用它，我们先来了解一下它的几个相关问题.

故事背景：皮耶·德·费马（Pierre de Fermat）是17世纪的一个法国律师，也是一位业余数学家.之所以称其业余，是由于皮耶·德·费马具有律师的全职工作.

费马点定义：指位于三角形内且到三角形三个顶点距离之和最短的点.它是皮耶·德·费马发现的，因而称之为“费马点”.

费马点的结论：

（1）对于一个各角不超过120°的三角形，费马点是对各边的张角都是120°的点.

托里拆利的解法中对这个点的描述是：对于每一个角都小于120°的△ABC的每一条边为底边，向外作等边三角形，然后作这三个等边三角形的外接圆.托里拆利指出这三个外接圆会有一个共同的交点，而这个交点就是所要求的点.这个点因此也叫做托里拆利点.如图1，在△ABC中，当∠APB=∠APC=∠BPC=120°时，AP+BP+CP取得最小值.

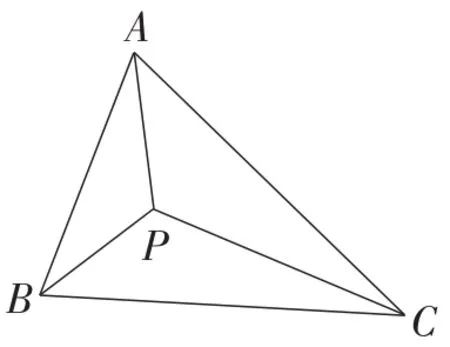
图1

（2）若三角形有一个内角大于等于120°，则此钝角的顶点就是距离和最小的点.

二、今生

费马点问题的主要解决方法是通过旋转变换来改变线段的位置，从而达到优化图形的效果.但试卷上呈现出来的除了平铺直叙的运用外，还会运用旋转这一主要思想精髓来命题，将这类问题的相关信息融入到综合题中，去考查学生的空间想象能力，以及实践探究能力.这会让很多学生对此类问题束手无策，甚至不敢触碰.所以教师讲解这类问题时，除了讲清问题的来龙去脉，更要讲清问题解决的主要精髓，并引导学生养成对问题深入探究的习惯.

笔者对“费马点模型”深入研究发现，常有以下几种情形可以用旋转来解决：

①3条线段的系数都为1；

②1条线段的系数不为1；

③2条线段的系数不为1；

④3条线段的系数不为1.

下面就一道题目来剖析一下各种可能情形的解决策略.

例1如图2，点D是等腰直角三角形ABC内一动点，已知.求：

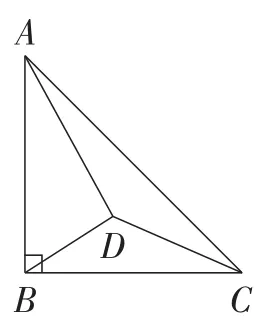
图2

（1）求AD+BD+CD的最小值；

（9）求3AD+4BD+5CD的最小值.

第一种情况：三条线段的系数都为1的情形.

第（1）小题这种情况，是最直接的运用，主要是用“费马点问题”的主要解题策略，即旋转图形，改变线段的位置，这也是要找相等线段常用的方法.如图3，把△ACD绕着点C旋转60°，此时有CD=DD′，AD=A′D′，BD保持不动，要想使得DA+DB+DC的值最小，只有A′D′，DD′，DB三条线段在同一条直线上，如图4所示，求出线段A′B的长即为最小值.

求A′B的长度主要是抓住A′A=A′C，AB=BC，可以判断此时A′B垂直平分AC于点H，进一步可求得∠CBH=45°，∠CA′H=30°，接下来的计算也就顺理成章了.根据条件可求得

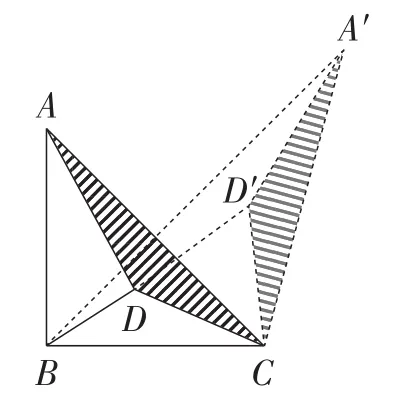
图3

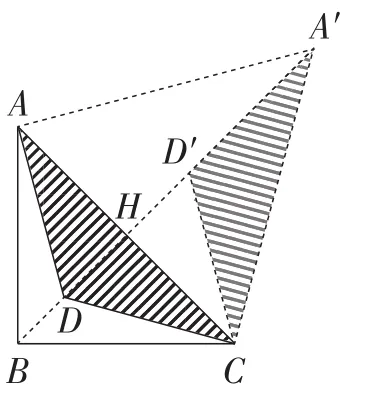
图4

这个问题还要想清楚：旋转中心是哪一点？旋转方向是什么？理论上绕△ABC哪个顶点都可以，只要将要旋转的△ACD向就近的边AC外旋转60°就可以了.但对于具体的题目还是要考虑到条件所给量，会带来不一样的运算量.这种问题需要有较强的推理能力和运算能力，这种题目也是训练运算能力的好题目.

读者也可以把其他顶点作为旋转中心，尝试构图与计算，在此不再赘述.

第二种情况：1条线段的系数不为1.

第（2）（3）小题这种情形，与“阿氏圆问题”“胡不归问题”一样的地方是如何将带有系数不为1的线段转化为系数为1的线段，所以可顺着上面的思路，先改变线段的位置，再考虑系数问题.这里可以通过三角形位似，以及直角三角形的边的比例关系来改变系数，这种情形的系数经常出现的是可以联想到等腰直角三角形的三边之比是，所以是旋转90°；可以联想到顶角为120°的等腰三角形的三边之比是，所以是旋转120°.然后再将三条线段共线（即两点之间线段最短），就可以求出最小值了，如图5、图6所示.

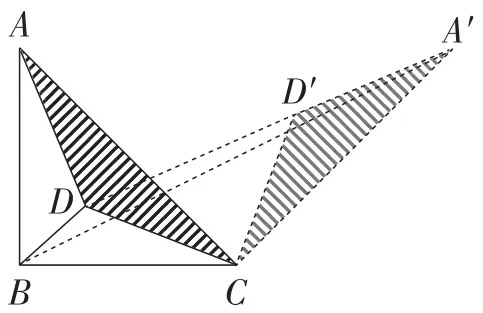
图5

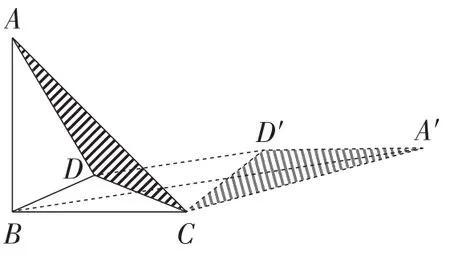
图6

至于计算，这种问题经常是用一线三等角相似（全等）、三角函数、勾股定理等即可求解.

不为1的系数能加在其他线段上吗？当然可以，谁加系数就转谁，不然会比较麻烦.

第三种情况：2条线段的系数不为1.

第（4）小题是双系数，这类问题由于初中知识的限制，所给的系数是有一定关系的，不难发现它们满足勾股关系BD的系数为1，不动.这样只能旋转△ADC，先来尝试以点C为旋转中心，并按上面问题处理的旋转方式来旋转一定的角度后，得到△A′CD′.再把A′D′以点C为位似中心放大2倍，就得到A″D″=2AD，此时CD″=2CD.如图7，当时问题得解.不难发现此时∠DCD′=60°，∠D″DC=90°，所以是旋转60°.这里△DCD″是直角三角形，主要是由“”的系数大小决定的.

图7

还要注意的是，旋转中心要定在哪个点？为什么旋转角为60°呢？旋转方向是什么？旋转中心可以是点A吗？当然可以.但此时旋转角大小就要改为90°，缩放比例就要改为倍.这个问题若是“悟”明白，这些问题也就清楚了！

图8

图9

图10

对于这类问题，主要是考虑把哪条线段的系数作为缩放的比例，再由另一个不为1的系数来决定旋转的角度（90°或60°或30°）. 若中间的线段（DD″）的系数是最大的，那就是旋转90°，否则就是60°或30°.

第四种情况：3条线段的系数不为1.

第（7）～（9）小题是三系数，一般三个系数都满足勾股关系，它可以通过提公因数的方法把三系数转化为双系数或单系数问题，然后按第（2）～（6）小题的方法来处理，要注意的是最后的结果需要乘所提取的系数.

这样的问题，其实只要系数是满足任意一组勾股关系的都是可以的.解决时主要是看好旋转中心，定好缩放比例.至于旋转角度，旋转90°比较多，有时也旋转60°或30°或120°.

为什么要是勾股数呢？其实也是受初中知识的限制，初中没有余弦定理，查表也无法计算对边长.

“费马点模型”解题思路：旋转、放缩、定线段、计算，即通过旋转变换，可以改变线段的位置，根据条件中的系数定缩放比例，再确定要求的线段（三“折”转一“直”），最后计算.旋转的角度经常是60°或90°或120°或30°.

三、来世

好问题的研究，不仅要研究它的解决策略，还要研究它解决问题的精髓是什么.费马点模型的精髓是旋转变换，改变线段的位置，优化图形.所以我们要学会用旋转来解决问题.在使用这一方法时需存在相等的线段，即当题目出现等腰三角形（等边三角形）、正方形条件时，可将图形作旋转变换，将不规则图形变为规则图形，或将分散的条件集中在一起，以便挖掘隐含条件，使问题得以解决.

例2如图11，设点P到等边三角形ABC两顶点A，B的距离分别为3，2.求PC的最大值.

图11

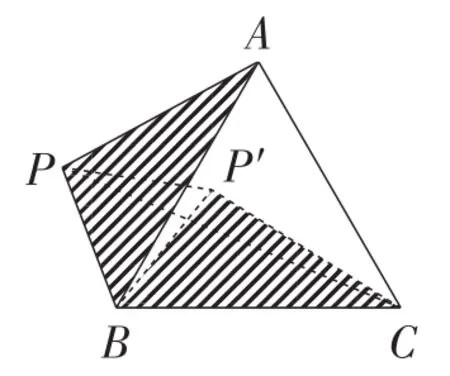
图12

解：如图12，连接PC，

将△ABP绕点B顺时针旋转60°，得到△BCP′.

则AP=CP′，BP=BP′.

根据“三角形两边之和大于第三边”可知，PC≤PP′+P′C（当P，P′，C三点共线时取等号）.

故PC的最大值为PB+PA=2+3=5.

变式：如图13，在四边形ABCD中，BC=CD，∠BCD=90°，AB=4，AD=3，求对角线AC的最大值.

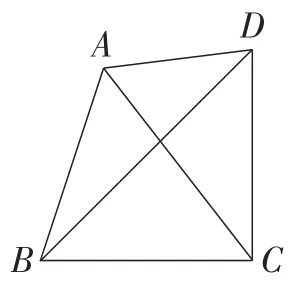
图13

【反思】这里主要是利用“费马点”旋转的解题思想，通过旋转改变线段的位置，从而达到优化图形的目的.当然这两道题都还可以用其他的旋转方法来解题.

教师对线段最值问题只研究到“将军饮马”问题这一层面是远远不够的.作为一线教师要让学生在处理几何问题时有模型意识，并且要让学生学得“宽、深、透”，力争让学生达成数学玩转模型、解题靠研究的境界.