基于动态时间规整的钢轨轨廓匹配方法
陆英杰, 朱洪涛
(南昌大学 机电工程学院,南昌 330031)
钢轨轨廓检测是确保高速列车行车安全的重要措施之一,准确地反映钢轨轨廓能够为铁路检修、病害预测提供切实的依据[1-2]。轨廓检测的主要目的是将测量得到的实际轨廓匹配到标准轨廓上,从而来分析钢轨的磨损情况和变形程度。因此,轨廓匹配方法成为钢轨轨廓检测过程中的关键问题之一。
目前,在轨廓匹配方法的研究中,Jin等[3]使用CSS角点检测算法提取钢轨轮廓曲线的拐点,通过特征点来校准轮廓数据,但这种方法对传感器抗噪性要求较高,很难适应复杂环境下的检测;Santur等[4]使用3D激光照相机来获取钢轨轨廓图像信息,再使用深度学习的方法来检测钢轨轨廓的磨损和缺陷,但这种方法计算量太大;Chen等[5]提出一种钢轨全断面自动匹配的方法,但未考虑特征点检测不到的问题;Molleda等[6]提出一种利用4个线激光传感器对单股钢轨进行检测的方法,将获取的点云进行拼接并利用ICP算法匹配到标准轨廓上去,这种方法可以获得完整轨廓,但是使用的传感器较多,且未进行实际应用,缺乏说服力;康高强等[7]先利用轨廓上两条不同斜率直线交点的方式提取特征点进行匹配,然后再利用ICP算法求出与标准轨廓的变换矩阵实现最终匹配,但是由于两条直线斜率相差不大且拟合点较少,特征不明显;占栋等[8]依据左右两股轨道的轨距点坐标变换,未对测量平面内的振动进行补偿。谭周文等[9]通过提取钢轨轨腰处两个已知半径的圆心作为特征点,利用坐标转换,计算旋转量和平移量,完成整个轨廓匹配,但是大圆弧的测量数据较少,且半径较大,计算精度不高。以上这些算法都是基于理想状态下,认为多组传感器刚体振动,且假设轨廓匹配基准段完好无损,未能解决实际情况中,传感器振动存在差异性,且匹配基准段特征点无法提取的问题。
本文采用线激光检测的方法采集轨廓数据,根据传感器标定值,利用坐标转换公式,将测量数据进行旋转和平移,统一到标准轨廓的坐标系下。通过Hough变换检测轨腰处已知半径的圆弧,得到三个圆心作为特征点,利用坐标转换公式计算出旋转角度和平移量,实现初步匹配。在此基础上,提出了一种基于动态时间规整的轨廓匹配算法,选取测量轨廓和标准轨廓的轨腰数据作为匹配基准,构造两个时间序列,计算距离矩阵,利用递归思想,获得累积代价矩阵,从而找到最优规整路径,得到两段数据之间各点的对应关系,实现测量轨廓和标准轨廓的精准匹配。
1 测量原理
测量系统主要是由线激光传感器、光电编码器、单片机、上位机组成,其系统结构如图1所示。该套检测系统属于动态轨廓测量,整个机构安装在轨检小车上。当上位机发出开始指令时,推动轨检小车运动,记录里程,触发激光传感器工作,投射结构光,采集钢轨轨廓数据并上传。
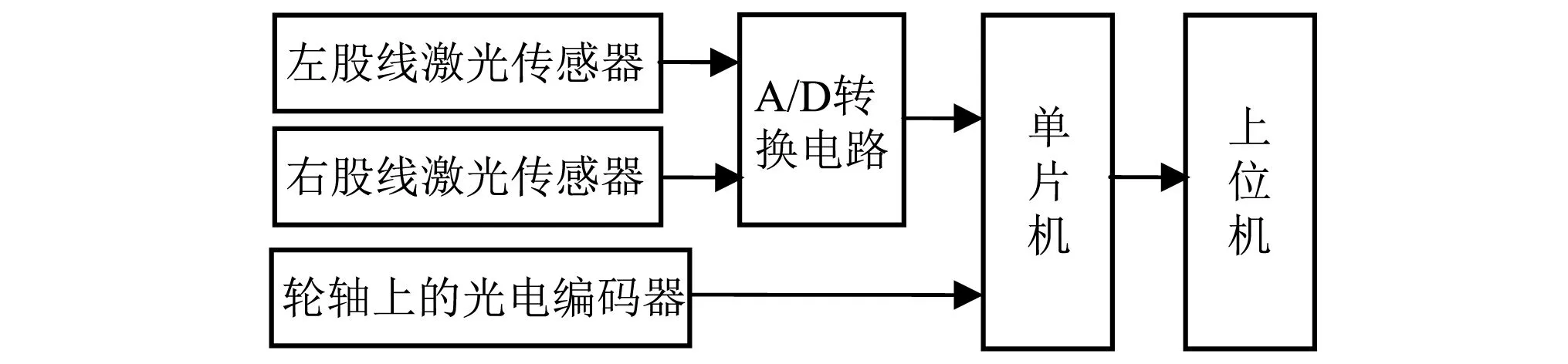
图1 测量系统结构图Fig.1 Structure diagram of measuring system
由于传感器测量范围有限,每股钢轨需要两组线激光传感器共同工作,才能获得完整的轨廓图像,一组线激光传感器由一个结构光源和一台CCD摄像机构成。因此,检测系统共需要4组线激光传感器,同时对左右两股钢轨进行轨廓测量,如图2所示。
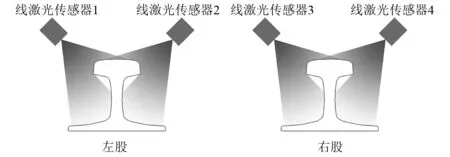
图2 钢轨轨廓检测示意图Fig.2 Structure diagram of measuring system
利用两组激光传感器去测量钢轨的断面轨廓,势必要求测量范围能够覆盖到钢轨的整个轨廓(除轨颚部分盲区)。因此,要将测量同一股钢轨的两组传感器对称安装在钢轨两侧,并确保两组传感器的结构光在同一平面上,这样才能实现对钢轨的高精度测量。
2 坐标转换
根据测量机构的特点可知,同一股钢轨的两组传感器以不同的角度去扫描钢轨轨廓,故采集的测量数据也是在各传感器坐标系(以下简称相对坐标系)里呈现出来的。只要传感器与钢轨的相对位置不变,测量数据就不受影响,因此无论钢轨断面绝对坐标系如何变化,都可以适用。如果将采集数据直接输入到标准轨廓的坐标系(以下简称绝对坐标系)中,则无法实现测量轨廓与标准轨廓的匹配,如图3所示。本文以60 kg/m钢轨为例,为了实现钢轨轨廓的精准匹配,需要对采集数据进行坐标系的转换,使两组采集数据的坐标系统一到一个坐标系下。

图3 标准轨廓与测量轨廓Fig.3 Standard rail profile and measurement profile
对于钢轨轨廓上的同一个点S,在两个不同坐标系XOY和X’O’Y’中,有不同的二维坐标(x1,y1)和(x2,y2),如图4所示。XOY坐标系相对于X’O’Y’坐标系顺时针旋转θ角,平移(xo,yo)。为了实现轨廓的精准匹配,利用坐标转换公式,将测量数据从相对坐标系统一到绝对坐标系中。
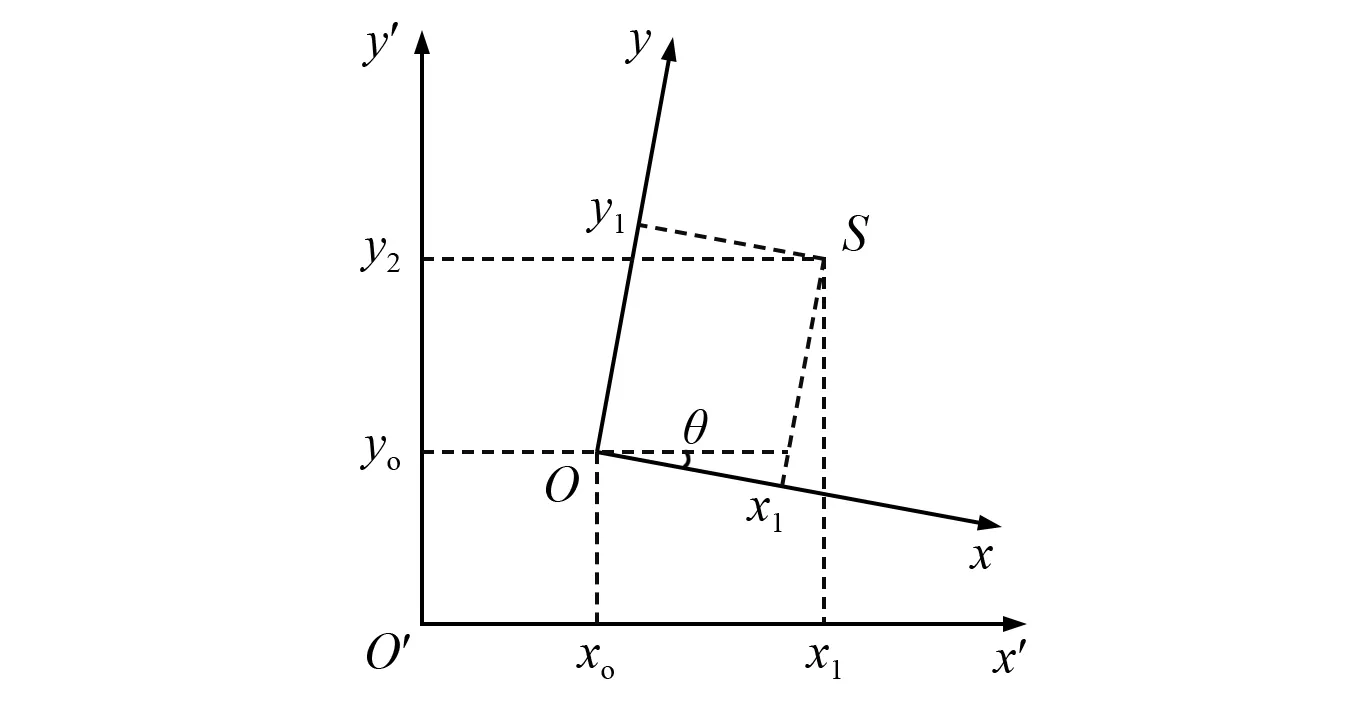
图4 坐标转换示意图Fig.4 Coordinate transformation diagram
根据图4中的几何关系,可以列出S点坐标在不同坐标系中的转换公式:
x2=x1cosθ-y1sinθ+xoy2=x1sinθ+y1cosθ+yo
(1)
将式(1)写成矩阵的形式为:
(2)
2.1 传感器旋转角度和平移量标定


表1 传感器旋转角度和平移量标定值Tab.1 Sensor rotation angle and translation amount calibration value
2.2 振动补偿
动态检测中,安装于轨检小车上的传感器,会跟随小车在行进中一起振动,从而使测量轨廓图形出现浮沉振动、左右振动、侧倾振动等多种不良情况[10]。在轨廓匹配初期,可将小车和传感器近似看成一个刚体,如图5所示。
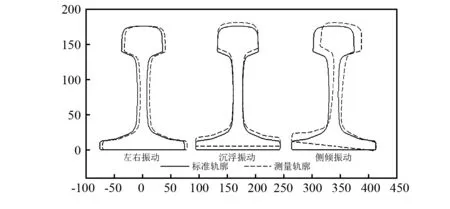
图5 振动的类型Fig.5 Types of vibration
根据上述情况分析可知,振动导致了测量轨廓的旋转和平移。在检测系统中,以标准60 kg/m轨为匹配模版,建立绝对坐标系,将钢轨断面底座作为横轴,钢轨中轴线作为纵轴。轨腰处不是磨损区,且存在已知半径的圆弧,故能用来作为匹配基准[11],利用Hough变换找到圆心A、B作为特征点,如图6所示。
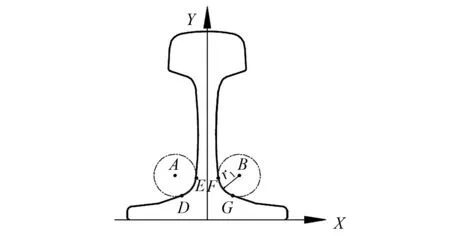
图6 特征点示意图Fig.6 Feature points diagram
Hough变换可以用来检测圆,并且能够找到圆心[12]。在平面中,圆的直角坐标方程可以表示为:
(x-a)2+(y-b)2=r2
(3)
式中:圆心坐标为(a,b),圆的半径为r,(x,y)为圆上的点。
Hough变换的基本思想是,利用点线对偶的方法,将数据平面中的点,对应到参数平面上的线。将式(3)改写成:
(a-x)2+(b-y)2=r2
(4)
式中:数据点(x,y)作为圆心,(a,b)作为圆上的点,若半径r已知,可以在参数平面画出一个圆。当参数平面上的两个圆相交时,证明此时的交点(a,b)同时满足这两个方程。将待检测的n个数据点全部作为圆心,在参数平面画出n个圆,通过统计特性,找出相交最多的峰值点,即为检测到已知半径的圆心(ao,bo),如图7所示。若半径r未知,可以设置r的阈值,并给定步长,利用迭代思想,以同样的方法搜索圆心。

图7 参数平面坐标系Fig.7 Parameter plane coordinate system
利用Hough变换,在标准轨廓EF和DG段搜索半径为20 mm的圆弧,得到两个圆心A(x1,y1)和B(x2,y2)坐标。类似的,可以获得测量轨廓的对应圆心A′(x1′,y1′)和B′(x2′,y2′)坐标。但是,由于钢轨局部生锈等问题,已知半径的圆心可能检测不到,这时,采用Hough检测未知半径圆心的功能,依然能够获得圆心。通过坐标转换原理:
(5)
求解出振动导致的旋转角度α和平移量(Δx,Δy),在根据式(2)对采集的数据一起进行振动补偿,消除振动对轨廓测量系统的影响,实现轨廓初步匹配。该坐标转换方法也可以推广到安装在列车上的高速轨廓检测系统。其传感器相对钢轨振动较大,且各种振动相互耦合,轨腰处的圆弧可能会被测量成椭圆圆弧。可将耦合振动按照不同基准坐标系分解,利用椭圆拟合算法,找出椭圆中心,与标准轨廓圆心对比,逆向计算出各种振动引起的角度和位移偏差,据此补偿传感器相对钢轨的振动。若有实验条件,可进一步研究。
3 动态时间规整算法
动态时间规整(Dynamic Time Warping)是一种基于动态规划思想的算法,该算法准确率高、鲁棒性强,被广泛应用在语音识别领域[13]。动态时间规整算法不仅可以实现数据点之间的“一对一”匹配,还可以实现“一对多”匹配,突破了数据点等长匹配的限制,可以对不同长度的时间序列进行匹配[14]。
在实际测量中,每个传感器的振动其实不是完全相同的,钢轨左右两侧的传感器在振动时存在一些差异,如图8所示,影响轨廓匹配效果。通过动态时间规整算法,可以有区别的补偿每个传感器的振动噪声,提高轨廓匹配精度。
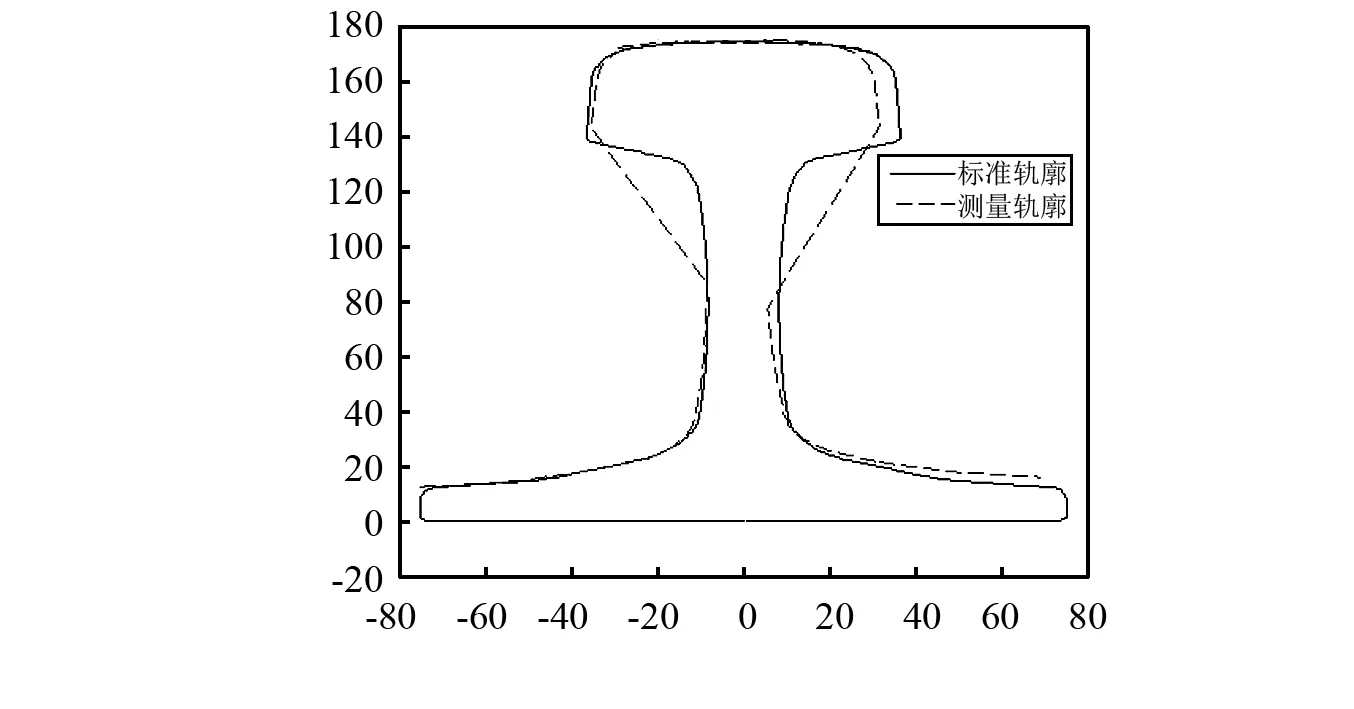
图8 两组传感器振动差异Fig.8 Vibration differences between two sensors
激光传感器是等距测量,每隔0.3 mm测量一个点[15]。所以,可以将横坐标看成时间轴,将纵坐标数据放入时间序列。从轨腰处选取初步匹配的对齐数据,分别放入两个时间序列:
S={s1,s2,s3,…,sn} 存放标准轨廓匹配处的n个数据
T={t1,t2,t3,…,tm} 存放测量轨廓匹配处的m个数据

(6)
矩阵中的元素D(i,j)表示两个时间序列中si和tj的匹配,动态时间规整的目的就是在距离矩阵中找到一条最优路径,即累积距离最小的路径,如图9所示。
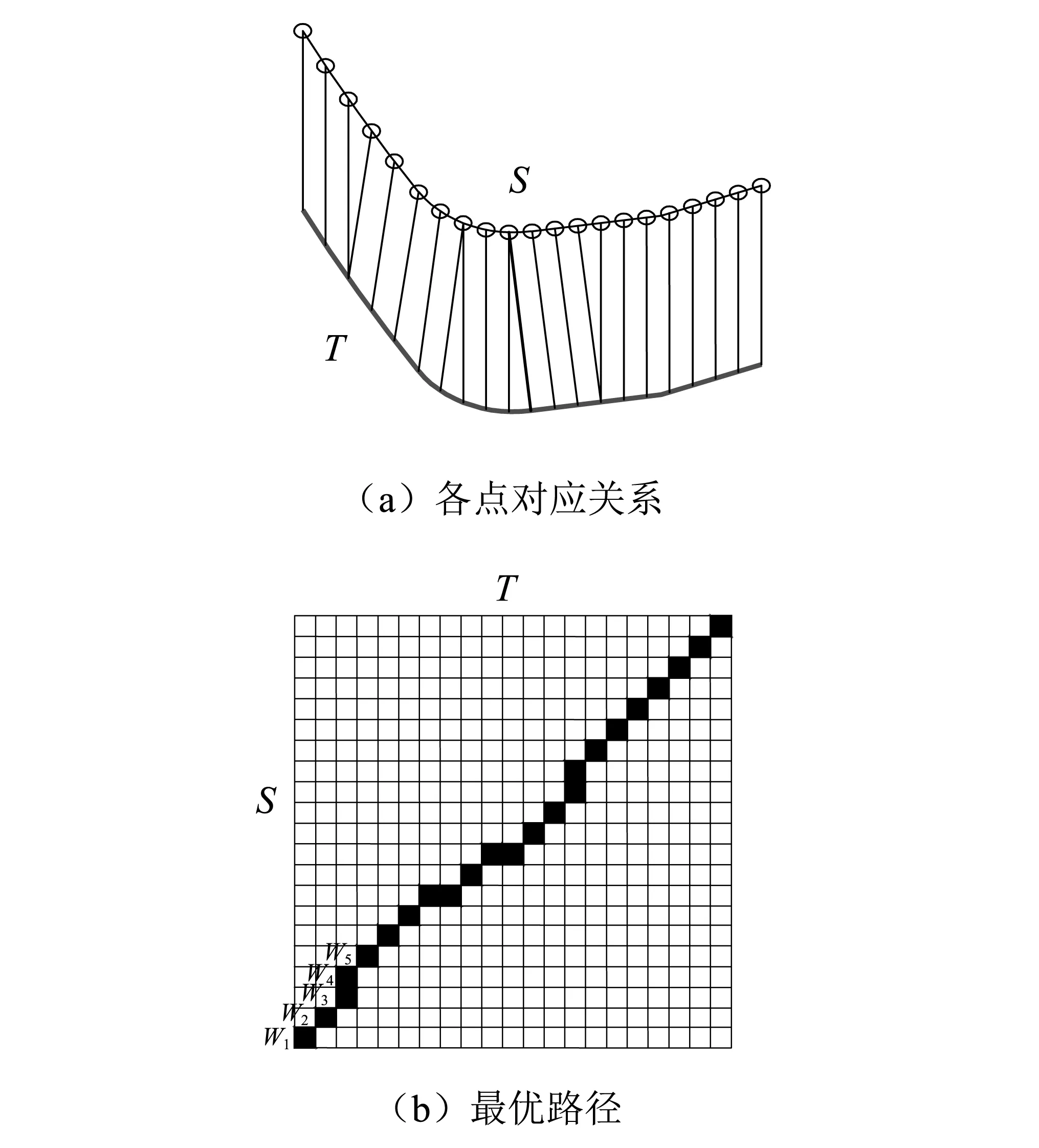
图9 各点之间的对应关系及最优路径Fig.9 Correspondences between points and optimal paths
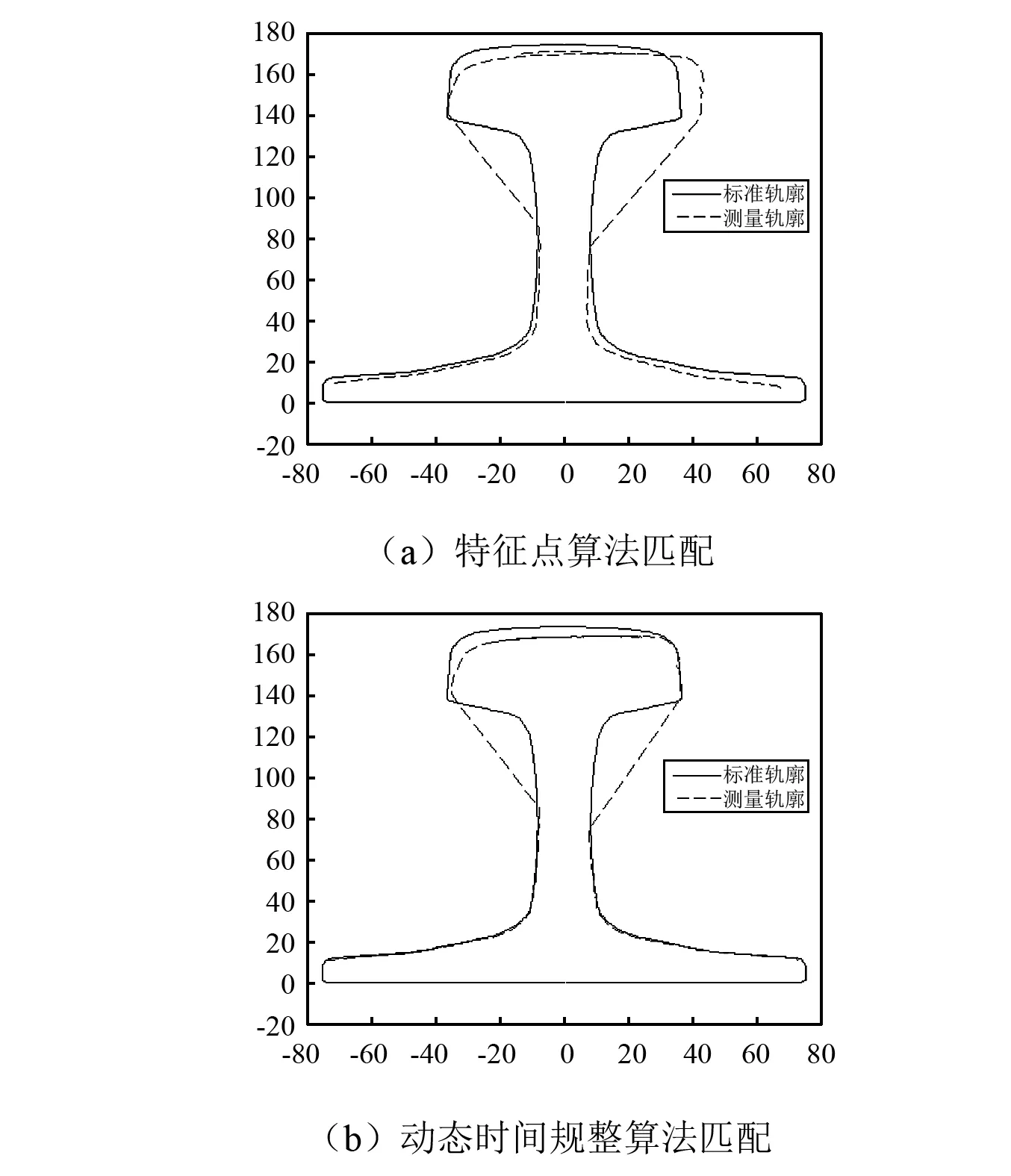
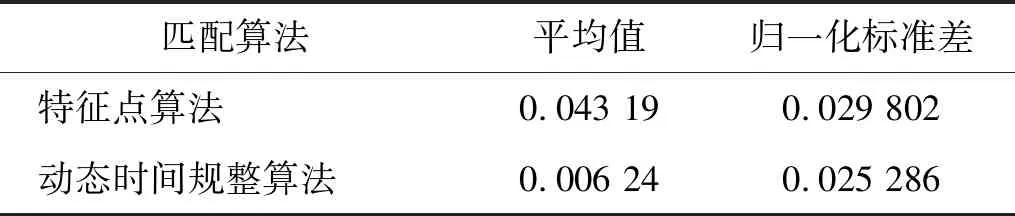
在距离矩阵D中,可以有很多条路径。这里使用W来表示规整路径:W={w1,w2,w3,…,wk,…,wK},max(n,m)≤K W={w1,w2,w3,…,wk,…wK}, max(n,m)≤K (7) W中的第k个元素定义为wk=(i,j)k,在距离矩阵中,路径的选择需要满足一下四个约束条件[16]: (1)边界条件:路径起点w1=D(1,1),路径终点wK=D(n,m); (2)连续性:路径上的两个相邻点wk-1=(a,b),wk=(c,d),则0≤|c-a|≤1,0≤|d-b|≤1; (3)单调性:如果wk-1=(a,b),则下一个点wk=(c,d)需要满足c-a≥0,d-b≥0; 根据上述约束条件可知,路径的走向可能有如下几种:从(i,j)点出发,走向(i+1,j)、(i,j+1)或(i+1,j+1),共有三种可能。因此,这样的路径会有很多条,需要找出使得规整代价最小的路径,即DTW距离: (9) 式中:K的作用是解决时间序列长度不一的问题。 为了求解式(8),利用动态规划的思想,构建累积代价矩阵γ,矩阵中任意元素求解为[17]: γ(i,j)=d(si,tj)+min{γ(i-1,j-1),γ(i-1,j),γ(i,j-1)} (9) 式中:γ(0,0)=0,γ(i,0)=γ(0,j)=∞。由式(9)可知,时间序列S,T的最小累积代价为γ(n,m),因此DTW(S,T)=γ(n,m)。 为了验证本文中匹配算法的可行性,利用自制的轨廓检测仪,在一条长期使用的磨损轨道上进行实验,如图10所示。 图10 轨廓检测实验Fig.10 Rail profile inspection experiment 基于本文提出的方法,对传感器采集到的轨廓数据进行相关处理。首先,根据激光传感器标定的旋转角度和平移量,利用式(2),对测量数据进行坐标转换,使同一股钢轨左右两侧传感器采集的数据统一到绝对坐标系下。然后,利用Hough变换找出轨腰处两个圆心A′和B′,利用式(5)求出振动引起的旋转角度α和平移量(Δx,Δy),进行振动补偿,实现轨廓初步匹配。最后,通过动态时间规整算法,选取测量轨廓和标准轨廓轨腰处100个点作为时间序列S和T,构造距离矩阵,找出最优路径,确定两个时间序列中各点的对应关系,并计算DTW值,完成轨廓的精准匹配,流程图如图11所示。 根据动态时间规整算法可知,两个时间序列的最优路径越小,即DTW值越小,它们相似性越高,因此,可以通过DTW值来反映轨廓的匹配效果。从激光传感器采集的数据可知,在钢轨轨头部分大概有80个点为重叠区域,即两组传感器测量了同一段区域,在理想状态下,匹配后这些点的拟合曲线应该是完全重合的,即DTW值为0。基于此,在完成轨廓匹配后,利用重复数据段中的80个点,计算其DTW值,作为实验结果的评价标准。分别利用传统的几何特征点算法和动态时间规整对轨廓进行匹配,如图12所示。 图11 轨廓匹配流程图Fig.11 Rail profile matching flowchart 图12 两种算法匹配对比Fig.12 Comparison of two algorithm matching 显然,经过动态时间规整算法处理的匹配效果更好,根据式(8)可以计算出两个算法匹配之后的DTW值,分别为0.034 3和0.007 4。为了证明本文提出方法的普遍性,对20组轨廓数据进行匹配,计算出DTW,并与特征点算法比较,如图13所示。 图13 DTW值统计Fig.13 DTW values statistics 根据图13中的数据,对这两种算法的DTW值进行分析,计算DTW平均值和标准差,如表2所示。 表2 DTW值统计分析Tab.2 Statistical analysis of DTW values 表2的数据表明,动态时间规整算法相比特征点算法的精度提高了近7倍,匹配效果提升明显。此外,从归一化标准差可以看出,动态时间规整算法的稳定性也较高。通过实验,证明了本文提出的动态时间规整算法很好地解决轨廓匹配问题。 在动态测量过程中,轨检小车的振动会影响轨廓匹配精度,而且不同传感器的振动情况存在着一些差异。此外,钢轨长期使用后,即使在非磨损区域,由于生锈等原因,几何尺寸也会发生微小的变化,影响匹配特征点的提取。基于动态时间规整的匹配方法,解决了传感器振动差异性补偿问题,同时弥补了特征点算法中由于体征点提取偏失而导致的匹配精度低的问题。实验数据表明: (1)基于动态时间规整算法的轨廓匹配精度达到0.006 24,是特征点算法精度0.043 19的近7倍。归一化后的标准差达到0.025 286,算法鲁棒性很好,完全能够满足轨廓的高精度匹配要求。 (2)当轨腰处出现轻微脏污时,如灰尘、油污等,由于轨腰处形状变化不大,匹配效果依然较好;当出现严重脏污时,如大块泥巴、树叶等,测量数据失真,会剔除数据并记录下此处里程,之后采用人工复测。 (3)算法计算效率较高,因为选取的两个序列不仅长度相同,而且经过初步匹配后,已大致对齐,只需计算某点与对应点附近几个点的距离进行比较即可。 (4)算法具有普遍适用性,不仅能用于直线段,也能用于曲线段。同时,还能适用于容易发生振动的道岔和波磨地段。此外,该算法可推广至其他领域,如轨廓接触式测量、钢轨测量里程对齐、轨道波形匹配等。4 实验及数据分析



5 结 论

