一道2019年高考模拟试题的探究与推广
北京首都师范大学数学科学学院(100048) 田朋朋
2019年北京市东城区高考文科第二次模拟考试压轴题题目如下:
试题已知椭圆C:=1 (a>b>0)的一个焦点为F(1,0),离心率为A为椭圆C的左顶点,P,Q为椭圆C上异于A的两个动点,直线AP,AQ与直线l:x=4分别交于M,N两点.
(1) 求椭圆C的方程;(2) 若△PAF与△PMF的面积之比为,求M的坐标;
(3) 设直线l与x轴交于点R,若P,F,Q三点共线,求证:∠MFR=∠FNR.
试题主要考查椭圆的标准方程、直线与椭圆的位置关系、椭圆中的几何性质等知识.考查数形结合、方程、转化与化规、函数与方程的数学思想方法以及运算求解能力.尤其是第三问,不仅可以通过将题干中的三点共线条件转化为斜率相等进行求解,还可以通过计算两向量数量积为零进行证明.但这两种方法计算量比较大,需要学生具有较强的运算能力.其实本试题有着射影几何的命制背景,我们可以从射影几何的角度来认识本试题的结构,认清其背后蕴含的丰富的数学背景.下面首先简单介绍一些射影几何中与二次曲线相关的基本理论.
1.射影几何中二次曲线的相关理论
定义[1]:如图1,点P为不在二次曲线上的点,过点P引两条割线依次交二次曲线于点E,F,G,H,连接EH,FG交于点N,连接EG,FH交于点M,则MN为点P对应的极线.特别地,若P是二次曲线上的点,则过点P的切线即为极线.同理直线PN为点M对应的极线,直线PM为点N对应的极线,MNP称为自极三角形.
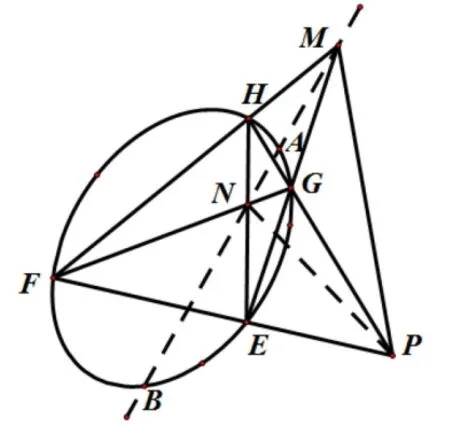
图1
(2)当点P为二次曲线外的点时,过点P作二次曲线的切线,切点分别为A,B.则点P的极线为直线AB.
(3)当点P为二次曲线内的点时,过点P引两条割线依次交二次曲线于点E,F,G,H,连接EH,FG交于点N,连接EG,FH交于点M,则MN为点P对应的极线.
在《高等几何》[2]一书中有:点P(x0,y0)关于二次曲线C:Ax2+Bxy+Cy2+Dx+Ey+F=0 的极线方程为
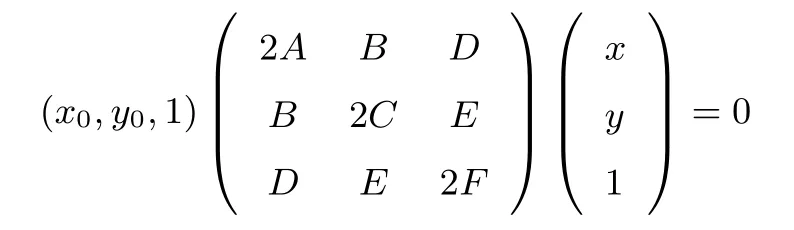
即(2Ax0+By0+D)x+(Bx0+2Cy0+E)y+Dx0+Ey0+2F=0.
特别地:(1) 对于椭圆C:=1,与点P(x0,y0)对应的极线方程为=1;
(2)对于双曲线C:,与点P(x0,y0)对应的极线方程为
(3)对于抛物线y2=2px与点P(x0,y0)对应的极线方程为y0y=p(x+x0).
事实上,圆锥曲线方程中,以x0x替换x2,以替换x,即可得到P(x0,y0)对应的极线方程.且可看出:圆锥曲线的焦点对应的极线为准线.
截至9月16日,49篇中国印刷产业改革开放大寻访文章已全部登完,得到业界高度关注并得到了强烈的反响。透过这些文章,通过镜头前的印刷人,我们发现,在科技飞速发展的当下,不确定的因素很多,印刷行业确也存在着各种困难和问题,而面对种种,大家依然以创新的精神一直行在路上,因为我们坚信,印刷业的使命是传承文明,传递美丽。
定理2[1]如果P点的极线通过Q点,则Q点的极线也通过P点.
2.解法探究与推广
解析(1)(2) 略.
(3) 如图2,椭圆C:的焦点为F(1,0),准线为x=4,点B为椭圆长轴上的右顶点.连接直线QB,则与直线l交于点M;连接直线PB,则与直线l交于点N,即△MFN为自极三角形.
此时设M(4,m),N(4,n),则点M(4,m)关于椭圆C的极线为直线NF,即NF方程为x+=1.又点N(4,n) 在直线NF上,因此有4+=1,即mn=-9.此时FR=3,即有MR·NR=FR2,即又因MR⊥x轴,所以有△MFR∽△FNR,因此∠MFR=∠FNR,证毕.
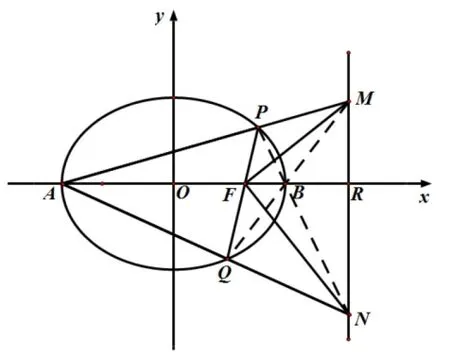
图2
由此可见,该试题为射影几何中的极点极线理论在圆锥曲线中的初等化表现.当改变试题中点A的位置或者直线PQ的位置时,其射影结构本质上不会发生改变,继续运用极点极线理论推理可得到如下推论.
推论1 已知椭圆C:=1(a>b>0)的右焦点为F(c,0),过焦点F的直线交椭圆C于P,Q两点,点A为椭圆C上任意一点(异于P,Q),直线AP,AQ分别交准线l:x=于M,N两点,则
(1)M,N两点的纵坐标之积为定值
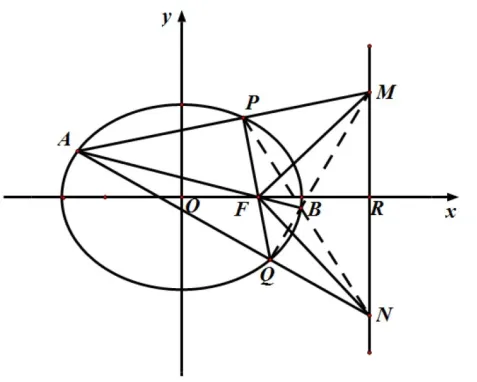
图3
(2)MF⊥NF.
证明如图3,点F(c,0) 关于椭圆C:的极线为准线连接直线AF交椭圆C于点B.连接直线QB,则与准线l交于点M,连接直线PB,则与准线l交于点N,△MFN为自极三角形.此时设则点M关于椭圆C的极线为直线NF,即NF方程为又点在直线NF上,因此有解得mn=此时因此有MR·NR=FR2,即又因MR⊥x轴,即△MFR∽△FNR,因此∠MFN=90o,即MF⊥NF,证毕.
推论2 已知双曲线C:=1 (a>0,b>0)的右焦点为F(c,0),过焦点F的直线交双曲线C于P,Q两点,点A为双曲线C上任意一点(异于P,Q),直线AP,AQ分别交准线于M,N两点,则
(1)M,N两点的纵坐标之积为定值
(2)MF⊥NF.
推论3 已知抛物线C:y2-2px(p>0)的右焦点为过焦点F的直线交抛物线C于P,Q两点,点A为抛物线C上任意一点(异于P,Q),直线AP,AQ分别交准线于M,N两点,则
(1)M,N两点的纵坐标之积为定值-p2.
(2)MF⊥NF.
推论4 已知椭圆C:过定点D(t,0)的直线交椭圆C于P,Q两点,点A为椭圆C上任意一点(异于P,Q),直线AP,AQ分别交直线于M,N两点,则M,N两点的纵坐标之积为定值
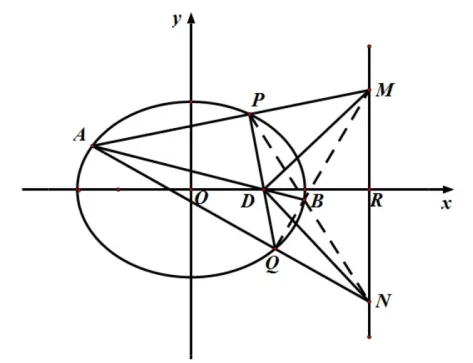
图4
证明如图4,点D(t,0) 关于椭圆C:=1 (a>b>0)的极线为直线连接直线AD交椭圆C于点B.连接直线QB,则交 准 线l于 点M;连 接直线PB,则交直线l于点N,△MFN为自极三角形.此时设则点M关于椭圆C的极线为直线NF,即NF方程为又点在直线NF上,因此有解得mn=证毕.
推论5 已知双曲线过定点D(t,0)的直线交双曲线C于P,Q两点,点A为双曲线C上任意一点(异于P,Q),直线AP,AQ分别交直线于M,N两点,则M,N两点的纵坐标之积为定值
推论6 已知抛物线C:y2=2px(p>0),过定点D(t,0)的直线交抛物线C于P,Q两点,点A为抛物线C上任意一点(异于P,Q),直线AP,AQ分别交直线l:x=-t于M,N两点,则M,N两点的纵坐标之积为定值-2pt.
推论2 和推论3 的证明可参考推论1 的证明过程,推论5 和推论6 的证明可参照推论4 的证明过程.

