全面开发教材例题习题 正确理解高考价值导向*——2019年高考全国Ⅰ卷理科第17题剖析

东莞实验中学(523120) 薛新建

一、原题呈现

题目(2019年高考全国Ⅰ卷理科数学第17 题)△ABC的内角A,B,C的对边分别为a,b,c,设(sinB-sinC)2=sin2A-sinBsinC.

(1) 求A；

(2) 若+b=2c,求sinC.

二、考纲分析

《2019年普通高等学校招生全国统一考试大纲(理科)》(下简称大纲)中对三角函数与解三角形部分要求如下：

1.突出考察形如y=Asin(ωx+φ)的函数图象与性质；考察两角和与差的三角函数公式和简单的三角恒等变换；

2.重点考察正弦定理、余弦定理及其应用,解决简单的三角形度量问题,以及与测量和几何有关的实际问题.

从2012-2018年高考对解三角形部分的考察来看,题型和位置都相对固定,对于“解决与测量和几何相关的实际问题”从来没有涉及,重点在于“解决简单的三角形度量问题”,y=Asin(ωx+φ)的函数图象与性质,以及三角恒等变换等的考察.这些问题类型主要包括利用对已知条件的边角互化求边或求角的问题,以余弦定理为载体考察三角形面积和周长问题,余弦定理与基本不等式结合求范围问题,正弦定理化一角一函数求范围问题等.与往年纵向比较,2019年解三角形的题目内容符合大纲要求,问题类型与往年规律相符(求角),学生通过正弦定理、余弦定理对条件进行边角互化后即可解决问题,题目定位容易题,对于整个试卷结构难易搭配的合理性起重要作用.经过仔细研究会发现,这一道解三角形题遵循经典但富有创新,定位简单然区分度高,看似复杂又源自教材,考察到的思想方法十分丰富,对学科核心素养的落实十分到位.

三、题目剖析

第(1)问对方程左边平方展开,得到三角函数的齐次方程,用正弦定理化角为边后再结合余弦定理可得下面重点分析第(2)问.

解法1

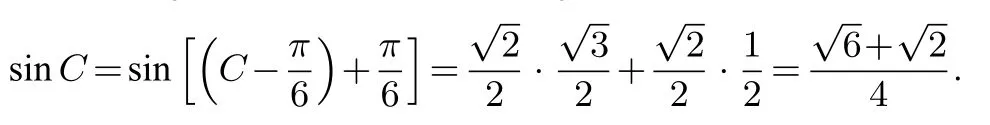
反思1 该解法中规中矩,从问题来看要求的是角,从条件来看所知是边,因此化边为角再结合消掉角B,即可得到关于角C的方程,后面通过简单构造将问题转化成常见的知值求值问题,既符合学生对三角函数的一般认知规律,也符合大多数师生平时的备考思路.这一常规解法证明该题定位清晰,难度适当,考察知识点合理合情,完全符合大纲要求.在实际运算过程中,学生可能把②式和sin2C+cos2C=1 联立去求sinC,计算得到sinC=或sinC=这两个解的取舍可以把sinC的两个值代入①去求sinB,进而发现sinC=时sinB=因此需要舍掉.这样的计算思路无论是解方程组还是对两个sinC的值的取舍,都会造成比较大的计算量,学生计算思路的选择可能会成为本题被诟病的原因.

解法2由(1)知A=,由余弦定理可得

与

联立消去b并整理可得两边除以a2得所以又由正弦定理知所以后同反思1 取sin

反思2 该解法是以余弦定理和题式联立消元得到a,c关系,抓住了两式的方程本质,三个变量两个方程经化简可以得到两个变量的比例关系,进而用正弦定理就可以转化为角.解法体现了函数与方程的思想,转化与化归的思想,考察了学生的逻辑推理和数学运算的核心素养.先消元再化角,符合大多数学生的思维习惯,但该解法运算量比较大,学生可能在运算过程中出错,放弃或者在最后对两个sinC的值的取舍时感到困难.值得一提的是,该解法有两个变解：即下述解法3 和解法4.

解法3在 ③④两个方程联立后,可以对两个方程选择主元进行思考,不要把方程组看成三元二次方程组,而是看成关于b的一元二次方程组.由 ③得

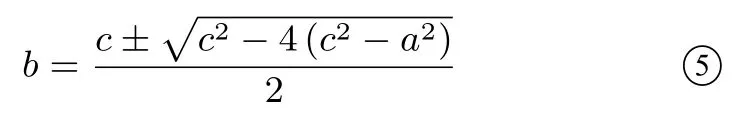
由 ④得

两式再消b得到a,c关系,后同解法2.

解法4在 ③④两个方程联立后,观察 ④式发现,成等差数列,不妨设即a=b=c+d,代入 ③式化简得c2+4cd+d2=0,两边除以c2进一步解得所以所以后同解法2.

反思3 解法3 和解法4 本质上与解法2 一样都是解方程,但一个大胆选定主元,发现了看问题的全新视角,一个建立等差数列模型,对方程进行转化解决,解决问题的主要过程同解法2 截然不同,体现了高考对创新性的要求.若是在平时的课堂上学生有这样的解题思路,无疑是应该被大力推崇的.

解法5如图1所示,延长AC至D,使延长AB至E,使BE=c,所以所以AD=AE,又因为A=所以ΔADE是正三角形,在三角形BCD中,∠BDC=由正弦定理可得所以从而由∠DBC所以故所以,从而

图1

图2

反思4 上述解法是从平面几何的角度,将和c长度的线段分别构造到AC和AB的延长线上,使得 ④式具有了几何意义,方法大胆新颖,让人耳目一新,是几何法解决三角函数问题的典型案例,整个过程体现了数形结合的思想和转化与化归的思想,考察了新课程标准中数学抽象,逻辑推理,数学建模,直观想象和数学运算等数学核心素养.这种解法也使本题在条件循规蹈矩的基础上,解答有了进一步发挥的空间,既体现了高考出题在知识交汇点处重点考察的特色,展示了知识之间的交叉、渗透和综合,又体现了高考试题越来越强的开放性和探究性的特色,给学生留足展示特色的舞台.

人教版《普通高中课程标准实验教科书数学必修5》(下简称教材)第18 页练习第3 题给出一组结论：在△ABC中,a=bcosC+ccosB,b=ccosA+acosC,c=acosB+bcosA.这组结论告诉我们三角形中任何一边等于其他两边在该边上的射影之和,结合图2很容易理解和证明,我们把这组结论称为△ABC中的射影定理.利用射影定理去看待本题则思路更为简单.

解法6由 ④式两边除以2 可得acosB+bcosA,把A=代入可得cosB=因为B ∈(0,π),所以所以所以

反思5 该解法直接应用教材配套练习中出现的射影定理去审视题目条件,将问题大大简化,运算量大大降低,该题源自教材这一事实,使得其定位简单题变得毫无争论,当然,这么简单的方法为什么大多数学生甚至老师都想不到呢? 这一点确实值得我们深刻反思.

四、对教学的启发

1.深度开发教材例题习题,培养学生核心素养.

教材是新课标精神的具体呈现,课堂是把新课标精神落实到学生身上的主阵地.教材中的例题是定理公理最典型的应用体现,课后的习题无疑也是对定理和例题最重要的补充,其巨大的教学价值尚待我们去发掘,其丰富的引领示范作用尚待我们去开拓.一些以习题资料为主要教学对象,把教材扔到一边的舍本逐末做法,我们应当及时摒弃.

比如前文中提到的射影定理,是一个符合常识的完美定理,我们在引入正弦定理的时候就可以设计这样的问题情境,让学生去摸索一并发现射影定理：如图2所示,我们在探索ΔABC中的边角关系的时候,借助辅助线CD⊥AB,可以在两个直角三角形ΔCAD和ΔCBD中发现CD=asinB,CD=bsinA,从而得到正弦定理,如果两个角都取余弦呢? 学生就会发现射影定理.让学生去体验发现和归纳的过程,就是新课标所说的“既要关注学生学习的结果,更要重视学生学习的过程”.实际上,这里还可以继续启发引导学生发现教材第20 页中的射影定理的变式：

2.深入研究新课程标准,提高自身理论修养.

新课程标准是党的教育方针在数学学科的体现,吸取了历次课程改革的高贵经验,也借鉴了国际课程改革的优秀成果,是具有国际视野的纲领性教学文件,其对学科核心素养的凝练,教学内容的更新,学业质量标准的研制,都具有划时代的意义,教材的更新也已经付诸实施.对教材的解读和使用成为新课程标准落到实处最重要的环节.这就需要一线教师及时更新观念,正确理解课程性质,准确把握课程理念,用培养学生学科核心素养的眼光去备课和展开教学.这样无论用什么样的教材,无论如何使用教材,都具有理论的高度和前瞻性.

3.及时学习学科考试大纲,把握高考最新动向.

高考是新课程标准最权威的指挥棒,考纲既是对新课程标准的凝练化体现,也是对高考最权威的指导意见,为二者起到重要的媒介作用.每年考试大纲的调整,都需要我们及时学习.比如现在高考把新课标的六大核心素养凝练成了理性思维,数学应用,数学探究和数学文化四项学科素养,把核心素养和高考能力整合为逻辑思维,运算求解,空间想象,数学建模和创新五种能力,新的试卷结构和新的试题类型也是呼之欲出.这些都是一线教师备考必须了解的新形势.