“一分为二”思想巧解一类函数问题——从2019年一道高考函数题说起

安徽省太湖中学(246400) 李昭平

1.从一道高考题看“一分为二”思想

题目(2019年高考全国Ⅰ卷理科第20 题) 已知函数f(x)=sinx-ln(1+x),f′(x)是f(x)的导函数.证明：f′(x)在区间内存在唯一极大值点.

分析本题跳出了过去常见的指数函数、对数函数、整式函数、分式函数的复合形式,而以三角函数与分式函数的复合型函数形式出现,这在近几年高考中还是首次,给人耳目一新之感.由于三角函数的导数仍然是三角函数,因此利用导数研究其极值也有一定的难度.显然,方程的实数根无法直接求出,这让我们联想到：能否将方程“一分为二”,利用两个函数和y=sinx的图象的交点个数来处理问题呢? 基于这种思路,得到下述解答.

解答因为所以由f′′(x)=0 得,sinx=画出函数y=和y=sinx的图象可知,在区间内两函数的图象有唯一交点,其横坐标是x0.

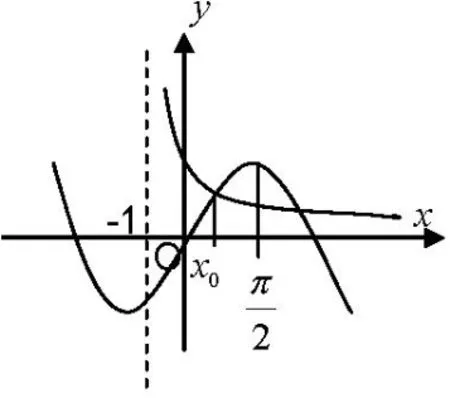
图1

显然,在x＜x0附近,在x＞x0附近,sinx＞,f′′(x)＜0.因此x0是函数的唯一极大值点.

结论由上述解答,得到以下结论：设函数f(x)=其中y=h(x)是定曲线或动曲线.则对于关于f(x)的能成立问题、恒成立问题、零点问题、极值问题、图象问题等等,利用“一分为二”的思想将复合型函数分成两条曲线y=h(x)和y=g(x),运用函数思想、数形结合思想、导数思想、动静变化思想和极限思想来处理,往往事半功倍.下面结合典例予以说明.

2.“一分为二”思想的几个应用

2.1 处理实根问题

例1(2016 高中数学联赛安徽省预赛题)若x2=aex恰有三个不同的实数根,则实数a的取值范围是____.

解析x2=aex就是a=x2e-x.令f(x)=x2e-x,则显 然f(x)在和(2,+∞) 内单减,在(0,2) 内单增,极大值是f(2)=4e-2,极小值是f(0)=0.当0＜a＜4e-2时,直线y=a与函数f(x)的图象有三个交点,故实数a的取值范围是(0,4e-2).

点评本题考查超越方程的实根,“一分为二”成两个函数y=f(x)(定曲线)和y=a(动直线),则问题立即转化为定曲线与动直线的位置关系,快速实现解题目标.一般地,设f(x)=h(x)-g(x),则f(x)=0 的实数根⇔f(x)的零点⇔f(x)的图象与x轴交点的横坐标⇔h(x)与g(x)图象交点的横坐标.

2.2 处理零点问题

例2(2019年浙江高考题) 已知a,b ∈R,函 数若函数y=f(x)-ax-b恰有三个零点,则( )

A.a＜—1,b＜0 B.a＜—1,b＞0

C.a＞—1,b＞0 D.a＞—1,b＜0

解析函数y=f(x)-ax-b恰有三个零点,就是方程f(x)=ax+b有且仅有三个实数根,即曲线y=f(x)与直线g(x)=ax+b有且仅有三个交点.f′(x)=x2—(a+1)x+a=(x —a)(x —1),f′(0)=a,f(0)=0.当a＜—1 时,直线g(x)=ax+b的斜率小于—1,与曲线y=f(x)只有一个交点(如图2),排除A,B.当a＞—1 时,如图3可知,在—1＜a＜0,b＞0 时,曲线y=f(x)与直线g(x)=ax+b不可能有三个交点,排除C.故选D.

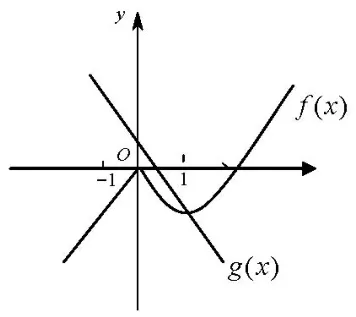
图2

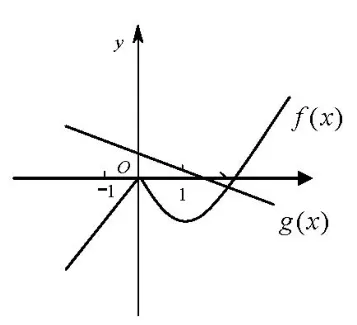
图3

点评由于函数方程中涉及a,b两个参数,按“一元化”思路不少考生会一筹莫展.仍然运用“一分为二”思想,转化为两个函数f(x)和g(x)的交点个数问题.根据选择题的选择支提供的信息,结合分段函数的图象,迅速排除错误答案.注意特殊与一般的关系是,一般寓于特殊之中.“命题在一般情况下为真,则在特殊情况下也为真”,“命题在特殊情况下为假,则在一般情况下也为假”.排除法、特殊化法是解某些非常规选择题的有效途径.

2.3 处理极值点问题

例3(2019年合肥市模考题)若函数f(x)=axlnx—ex存在唯一的极值点,则实数a的取值范围是___.

解析由题意知,f′(x)=alnx+a-ex=0 有唯一正实数根,即alnx+a=ex,令g(x)=alnx+a,h(x)=ex,其图象在第一象限只能有唯一公共点.

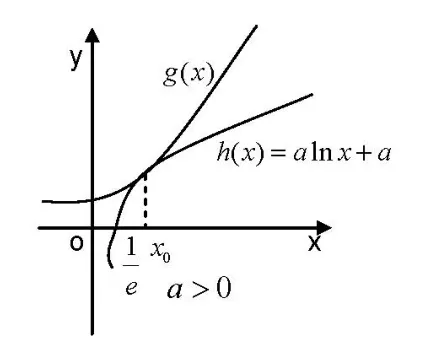
图4

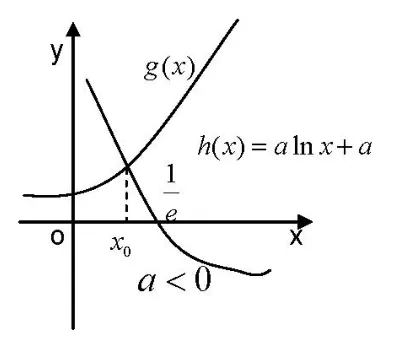
图5

当a＞0 时,在x0附近,始终有g(x)＞h(x),则f′(x)＞0,保号,此时x0不是f(x)极值点.当a＜0 时,在x0附近,f′(x)异号.此时x0是f(x)唯一的极值点.故实数a的取值范围是(-∞,0).

点评本题考查函数的极值点问题,是对数函数与指数函数的复合型函数,“一分为二”成两个函数y=g(x)(动曲线)和y=h(x)(定曲线),则问题立即转化为动曲线与定曲线的位置关系,结合极值点的含义(在极值点两旁附近f′(x)异号),确定参数a的取值范围.

2.4 处理恒成立问题

例4 (2019年济南市模考题) 设f(x)=xlnx,若f(x)≥kx-2(k+1)(k ∈Z) 对任意x＞2 恒成立,求整数k的最大值.

解析令g(x)=kx-2(k+1),显然直线g(x) 过定点(2,-2).利用导数可以画出曲线y=f(x) 的草图.由图象可知,直线y=g(x) 的极限位置是与曲线y=f(x) 相切,设切点是M(x0,y0),则切线方程是y-x0 ln x0=(1+ln x0)(x-x0).

将 点(2,-2) 代 入 得,2-x0lnx0=(1+lnx0)(2-x0),即x0-2 lnx0-4=0.则k≤1+lnx0.令h(x)=x-2 lnx-4,x＞2,则h′(x)=1-＞0,h(x)在(2,+∞) 内单增.又因为h(8)=6 ln 2-4=2(ln 8-lne2)＞0,h(9)=4 ln 3-5＜0,在x0-2 lnx0-4=0 中x0∈(8,9).于是故整数k的最大值是3.

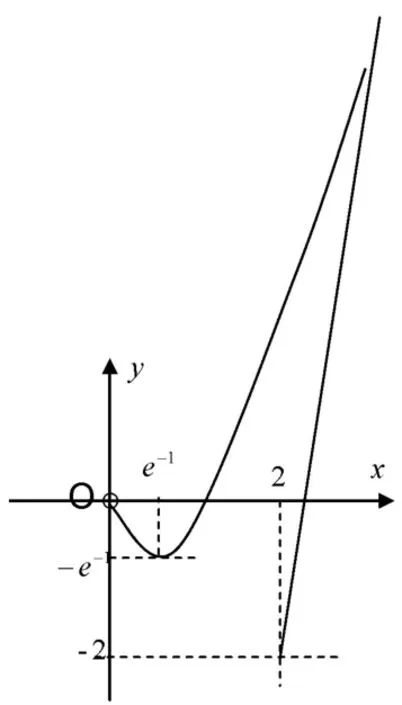
图6

点评本题考查恒成立不等式中整数参数的最值,是近期模考中出现的一种新题型,在继承传统的前提下,增加了思维深度和运算难度.利用“一分为二”思想,原不等式化成两个函数f(x)=xlnx(曲线大致形状利用导数确定)与g(x)=kx-2(k+1)(动直线,过定点),它们值的大小关系,则立即转化为定曲线与动直线的位置关系.整个过程体现了“数→形→数”之间的对应,直观想象、逻辑推理和数学运算三种核心素养贯穿其中.

2.5 处理切线问题

例5(2014年高考北京卷试题) 已知函数f(x)=2x3-3x.若过点P(1,t)存在3 条直线与曲线y=f(x)相切,求实数t的取值范围.

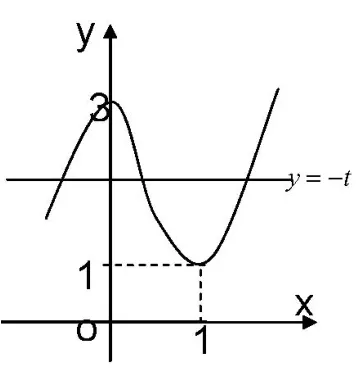
图7

解析设切点为A(x0,y0),则y0=2x30-3x0.因为f′(x)=6x2-3,所以f′(x0)=6x20-3,则切线方程是y-y0=f′(x0)(x-x0),即t-

点评这里如果从函数φ(x)=4x3-6x2+t+3 有三个零点出发,求导、求极值运算、画图中都要涉及到参数t,这比“一分为二”成“定曲线y=g(x)与动直线y=-t有3 个不同的交点”复杂得多.

上文给我们的启示是：好的高考题往往具有典型性、示范性和拓展性,如果教师认真思考、认真研究、认真比较,就能从中得到有价值的东西,并在课堂教学中恰当的运用,提升课堂教学层次.