2019年全国Ⅰ卷理科第19题的解法研究与推广
广东省湛江一中培才学校(524037) 魏 欣
广东省雷州市第八中学(524232) 邓春梅
高考中考查直线与圆锥曲线的位置关系的问题是常考的题型,久经不衰.此类问题计算量较大,尤其是多元字母运算,是考生的难点.纵观近年来的高考题,在解析几何中,直线与圆锥曲线相交时常把直线设成y=kx+b或x=my+t代人圆锥曲线方程中消元,代入圆锥曲线方程,应用韦达定理、求根公式与弦长公式求解.本文对高考中的直线与圆锥曲线的位置关系的问题进行了性质研究,通过剖析2019年全国Ⅰ卷理科第19 题的特点,提炼出针对性的解法,帮助学生把握问题本质、提高思维品质.使学生在问题解决的过程中发展数学抽象、逻辑推理、数学建模、数学运算、直观想象等数学核心素养,体会数形结合、等价转化等数学思想.
一、试题展示与评析
题目(2019年全国Ⅰ卷理科第19 题) 已知抛物线C:y2=3x的焦点为F,斜率为的直线l与C的交点为A、B,与x轴的交点为P.
(Ⅰ) 若|AF|+|BF|=4,求直线l的方程;
(ⅠⅠ) 若=求|AB|.
评析本题以解析几何最常见的抛物线为载体,考查抛物线的简单几何性质、直线的方程、斜率,直线与圆锥曲线相交的弦长等综合问题;在解题过程中,将问题坐标化,将交点化归为方程组的解,通过消元得到一元二次方程,涉及到函数与方程、数形结合、转化与化归思想,以及代入法和消元法等重要数学思想方法,重点考查数学运算、逻辑推理和直观想象等核心素养.
二、解法探究
解析(Ⅰ) 设A(x1,y1)、B(x2,y2)、P(t,0)(t>0),则直线l的方程为:对于抛物线y2=3x,所以由抛物线定义知所以
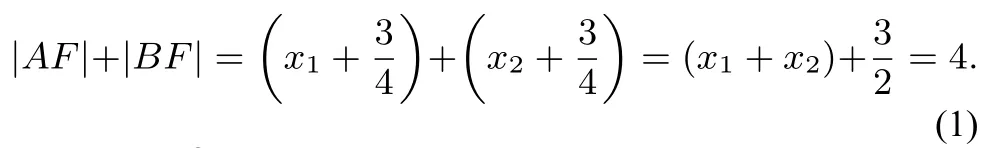
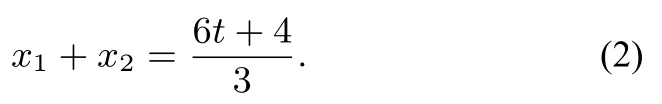
(ⅠⅠ)解法一设A(x1,y1)、B(x2,y2)、P(t,0)(t>0),因为所以-y1=3y2,即y1+3y2=0.因为直线l的斜率为所以设l的方程为由得y1=-3y2.联立得y2-2y-3t=0.即解得t=1.所以
(ⅠⅠ)解法二设A(x1,y1)、B(x2,y2)、P(t,0)(t>0),因为所以-y1=3y2,即y1+3y2=0.由得y2-2y-3t=0.所以所以解得t=1.所以即所以所以
(ⅠⅠ)解法三设A(x1,y1)、B(x2,y2)、P(t,0)(t>0),则直线l的方程为
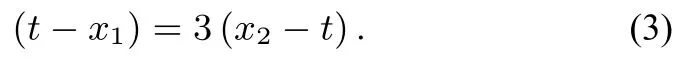
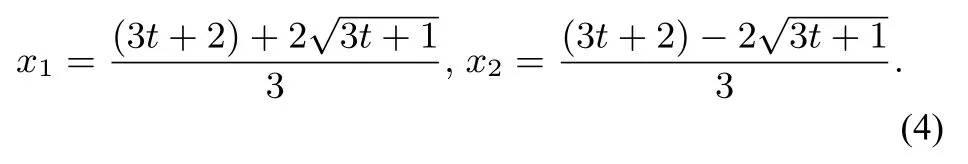
将(4)式代入(3)式,得
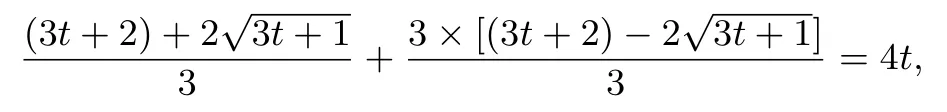
评析在第二问中,首先将向量问题坐标化,将交点化归为方程组的解,通过消元得到一元二次方程.然后设而不求,通过根与系数的关系进行求解.在求解的过程中,采用设直线方程为或代人圆锥曲线方程中消元,设直线方程为的形式来简化运算,减少运算量.一般来说,设过x轴上的直线方程时,设为方程x=my+n的形式与设y=kx+b的形式相比,运算较为简单,应该引起足够的重视.
二、教材寻根
高考题的命题有些是来源于教材,但往往又高于教材,因而我们的课堂教学需要回归教材,扎根教材,根深才能叶茂,源远方能流长.2019年全国Ⅰ卷理科第19 题来源于新课标人教A 版选修1-1 第61 页例4 题.教材是命制高考试题的一个源头,这也符合“源于教材,高于教材”的命题理念,这就要求我们了解高考试题的来龙去脉,领悟教材和高考试题的功能,这对跳出题海,正确把握高考复习方向,有着重要的意义和作用.
题目(新课标人教A 版选修1-1 第61 页例4)斜率为1的直线经过抛物线y2=4x的焦点,且与抛物线交于A、B两点,求|AB|.
教材中的例、习题具有典型性与代表性,能有效检查学生对重点知识的掌握及灵活应用的程度.分析历年的高考试题,可以发现,很多高考试题的原型都来自于课本教材,适当地进行一些改编和创新.高考的命题指导思想中也指出,要考查学生对基础知识、基本能力的掌握程度和运用所学知识分析、解决问题的能力.因此,对教材例、习题的探究是高考备考复习的重要方式之一.
三、结论研究
结论一已知抛物线C:y2=2px的焦点为F,斜率为k的直线l与抛物线C的交点为A、B,与x轴的交点为P.
(Ⅰ) 若|AF|+|BF|=m(其中m≥2p,m为常数),则直线l的方程为y=kx-其中直线l过
证明(Ⅰ) 设A(x1,y1)、B(x2,y2)、P(t,0)(t>0),则直线l的方程为由抛物线定义知|AF|=所以所以

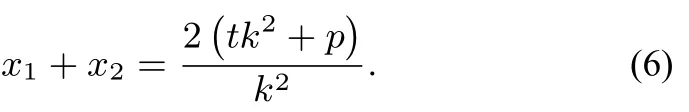

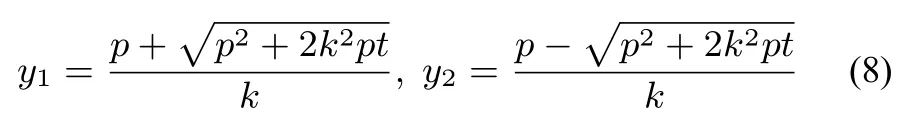
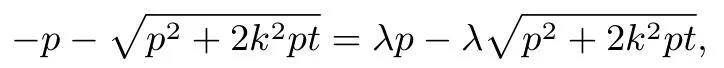
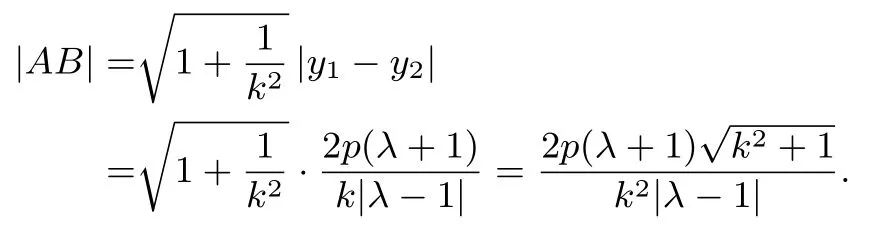
结论二已知抛物线C:y2=2px(p>0),过P(t,0)的直线l交C于A,B两点,且l的斜率则
(1) 当P位于A、B之间时,
(2) 当P位于A、B两侧时,
证明(1) 当P位于A、B之间时,设A(x1,y1)、则 直线l方程为x=my+t.因 为所以所以联立得所以同理,可以证明(2).
结论三若二次曲线过点P(t,0)的直线l交C于A,B两点,且l的斜率则
(1) 当P位于A、B之间时,
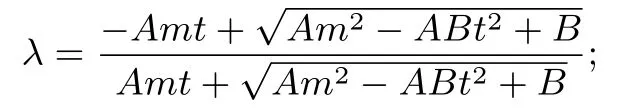
(2) 当P位于A、B两侧时,
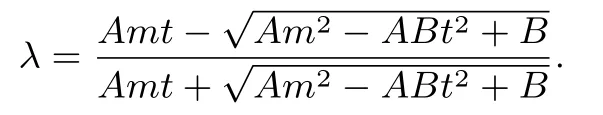
证明(1) 当P位 于A、B之 间 时,设A(x1,y1)、则直线l方程为x=my+t.因为所以所以联立得所以
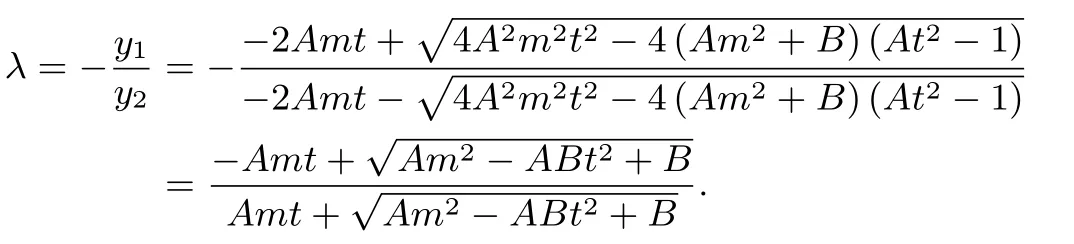
同理,可以证明(2).
结论四对于特殊的二次曲线Ax2+By2=0(AB<0且为常数),过点P(t,0) 的直线l交C于A,B两点,且l的斜率则
(1) 当P位于A、B之间时,
(2) 当P位于A、B两侧时,
证明(1) 当P位于A、B之间时,设A(x1,y1)、则直线l方程为x=my+t.因为所以所以联立得(Am2+B)y2+2Amty+At2=0.
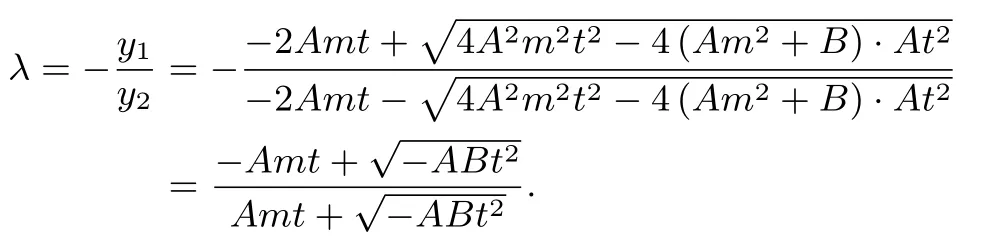
同理,可以证明(2).
四、真题回顾
由以上结论不难发现,在2013年全国ⅠⅠ卷文科第10题、2019年全国Ⅰ卷理科第10 题、2019年全国Ⅰ卷理科第16题,都源于以上圆锥曲线的性质结论,均可以用上述的通性通法来解答,体现了高考试题“常考常新,推陈出新”的理念.由于篇幅关系,此处只作简析.
1.(2013年全国ⅠⅠ卷文科第10 题)设抛物线C:y2=4x的焦点为F,直线l经过F且与抛物线C交于A、B两点.若|AF|=3|BF|,则直线l的方程为( ).
A.y=x-1 或y=-x+1
B.y=或y=
C.y=或y=
D.y=或y=
解由结论一,p=2,λ=3,F(1,0),代入直线l经过定点所以所以解得所以直线l的方程为或故选择C.
2.(2019年全国Ⅰ卷理科第10 题)已知椭圆C的焦点为F1(-1,0),F2(1,0),过F2的直线与C交于A,B两点.若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为( ).
解所以|AF2|=a.即A为椭圆的上顶点或下顶点.不妨设A为上顶点,由结论三,即t=1,常数A=常数B=且 点F2位于点A,B之间.即代入c=1,得a2=3.所以椭圆C的方程为a2=3.故选择B.
3.(2019年全国Ⅰ卷理科第16 题)已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1、F2,过F1的直线与C的两条渐近线分别交于A、B两点.若则C的离心率为____.
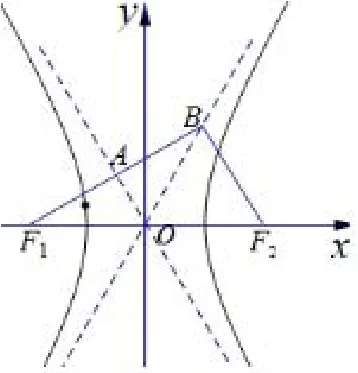
图1
解如图所示,双曲线的渐近线方程分别为由A、O分别为F1B、F1F2的中点,利用结论四,所以AB的斜率为即常数常数且点F1位于点A、B两侧.代入λ=得
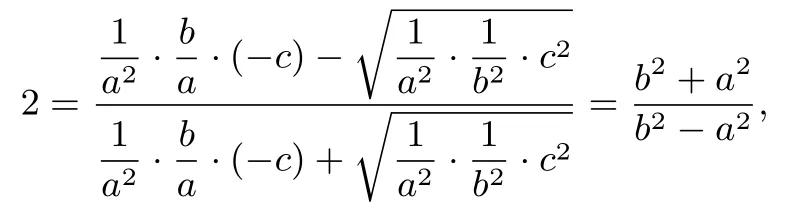
所以b2=3a2,即故双曲线的离心率为e=2.
五、备考建议
G.波利亚有句名言:“掌握数学就是意味着善于解题,如果我们在日常的教学中,能对课本例习题作深入的研究,一题多解,一题多变,多题一法进行变式教学,立根课本,必定能取得丰硕的成果”.
在数学教学中,我们要善于挖掘教材的潜在教学功能.教材中有一些典型性题目,它们或者是重要的结论,或者体现某种数学思想方法,或者是某个一般数学命题的具体形式,它的延伸、转化和拓广,可以呈现出丰富多彩的数学内容.我们必须充分重视课本典型例题、习题的探究,这是“用教材教”之根本,也是教师专业成长的必有之路.
随着新一轮高中课程改革的实施,教师对解析几何的教学应由传统的“结果性教学”转变为素养立意的“过程性教学”,这就要求教师在教学过程中,不仅要让学生知其然,更要知其所以然,同时引导学生了解甚至主动去探究解析几何问题的本“源”,学会举一反三,而不是就题解题,机械模仿.一方面,教师探寻解析几何问题的本“源”,追溯数学思维发展的源泉,可以提升教师自身数学专业素养和专业化水平;另一方面,教师把握解析几何问题的“流”[4],可以培养学生多维度思考问题的习惯,登高望远,拓展视野,如全国ⅠⅠ卷的第(ⅠⅠ)问,能够培养学生思维的深度和广度,提高学习数学的兴趣,挖掘数学学习的潜能.

