对2019年全国Ⅰ卷理数第23题的赏析

广州大学附属中学(510006) 陈经纬

题目已知a,b,c为正数,且满足abc=1,证明：

(2) (a+b)3+(b+c)3+(c+a)3≥24.

在课本《不等式选讲4-5》中,贯彻本书重要内容是基本不等式(包括两个或多个正数的),绝对值不等式、柯西不等式,所以本题考查基本不等式是情理当中的,也是符合新课标精神的,本题两问均可利用基本不等式证明,参考答案如下：

方法一(1) 因为a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ac,又abc=1,故有a2+b2+c2≥ab+bc+ca=所以

(2) 因为a,b,c为正数且abc=1,故有(a+b)3+(b+当且仅当a=b=c时等号成立.

点评虽说基本不等式可以完整地证明此题,高考题区别一般模拟题的一个重要特征就是解题入口比较宽,可以从不同角度处理,例如本题中第(1)问,考虑到不等式右边是平方式,容易联想到柯西不等式；

第(1)问相对较简单,以下重点讨论第(2)问,我们都清楚不等式是选考内容,有些高中侧重极坐标与参数方程教学,淡化不等式,导致部分考生即使学习过三个正数的基本不等式,也不能够灵活运用,本题最大的亮点是使用两个正数的基本不等式也可以解决；

方法二因为a,b,c为正数且abc=1,故有(a+b)3=

同理

二要认真落实云南与周边省区市及长江沿岸省区市签订的战略合作协议，深入推进与长江流域、成渝经济区和周边省区的交流合作，加强资本引进、渠道建设、市场对接，深度开展资本和产业合作。

点评解题成功的关键要素是代数变形的灵活应用,本题中技巧是将3 次降为2 次处理,若变形能力足够强大,再退一步,此题仅用初中的知识也可以解决.

方法三(a+b)3+(b+c)3+(c+a)3

根据(1)问得

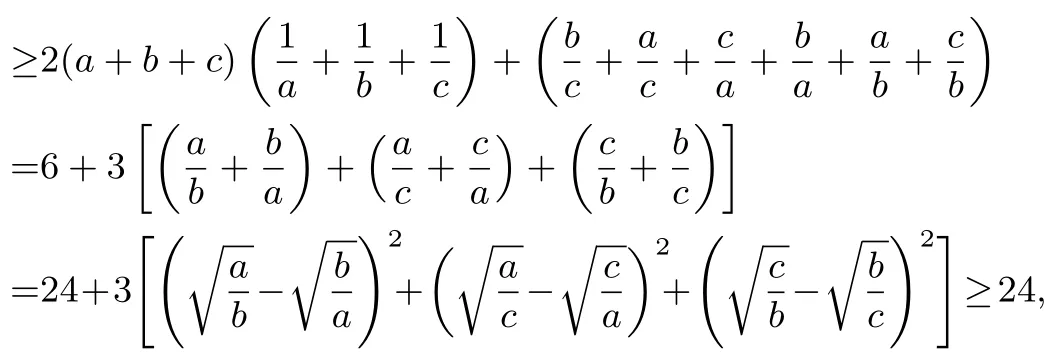
当且仅当a=b=c时等号成立.

点评运用此方法虽然只需要具备初中知识,但变形技巧要求高,对于高中生来讲有点绕圈子,不推荐使用.此方法的介绍,主要目的是让我们感受数学的美.

我们在学习导数的时候不可回避地接触到函数的凹凸性,由函数的凹凸性衍生出来的琴生不等式也可以很好地证明此题

琴生不等式

若f(x) 在区间I上为凸函数,则对x1,x2,···,xn ∈I,总有当且仅当x1=x2=···=xn时取等号.

方法四构造函数f(x)=x3(x＞0),因为f′′(x)=6x＞0,所以f(x)在(0,+∞)是递增的凸函数,即整理得当且仅当a=b=c时等号成立.

有一定竞赛基础的考生都知道权方和不等式是一个锐利小巧的不等式,它具有条件简明、结构优美、使用方便等特点,本题也可以使用权方和不等式证明；

权方和不等式

已知a1,a2,···,an,x1,x2,···,xn均为正数,若m＞0,则有

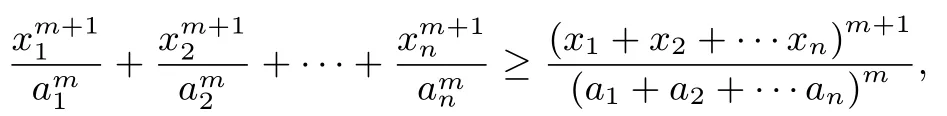
方法五(a+b)3+(b+c)3+(c+a)3当且仅当a=b=c时等号成立.

结束语

笔者所处的广东省采用全国Ⅰ卷,据了解,在选做题的处理上大部分中学都鼓励学生选择极坐标与参数方程,

由于不等式选讲内容长期得不到足够的重视,而今年全国Ⅰ卷的极坐标与参数方程突然难度加大,整个考生一片“哀嚎”.

本文采用五种方法对2019年不等式选讲高考题进行多角度分析,充分说明不等式选做题的命制有一定的规律,解决方法也是多种多样的,同时不等式与高中数学其他板块内容结合比较紧密,特别是解决最值问题,有独到的优势,学好不等式对后续的学习也有很大的帮助.所以在今后的教学中,我们一线教师一定要对不等式选讲的教学加以重视.