外接球问题的本位探究

东华理工大学(344000) 汕头市潮阳第一中学(515100) 刘叶丛

外接球问题不仅促使数学抽象和直观想象相结合,考察逻辑推理和数学运算,而且充分展示球这个几何体的本质,很好地考察学生的数学学科素养,深受命题者的喜爱,是高考和各类模拟考甚至自主招生考试的高频考点.据统计,在2011年、2012年、2013年、2017年、2019年全国一卷的数学试题中均有涉及.

本位指本来的位置,比喻原始的地位,神话中常有下凡仙佛回归本位的说法.外接球问题灵活多变,确定球心的位置是解决此类问题的切入点,也是解题的难点[1].我们要抓住几何体外接球球心的本质特征：

(1) 到几何体各个顶点距离相等的点即外接球球心；

(2) 外接球球心是任意两条直径的交点；

(3) 外接球球心在几何体任意一条棱的中垂面上；

(4) 外接球的球心在经过几何体任意一个平面的外心且与此平面垂直的垂线上.基于此,本文结合实例对最常见的三类外接球问题及其表现形式进行本位探究,以供大家参考.

一、圆锥的外接球及其表现形式的本位探究

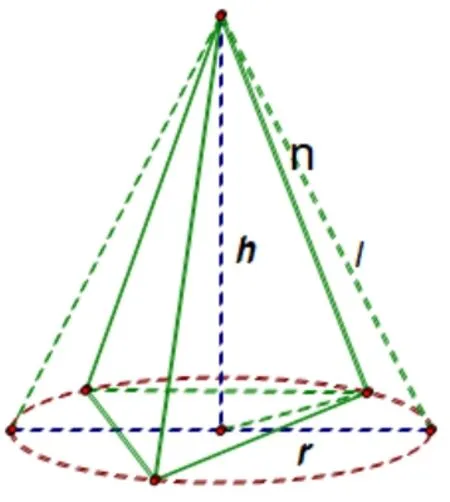
图1-1

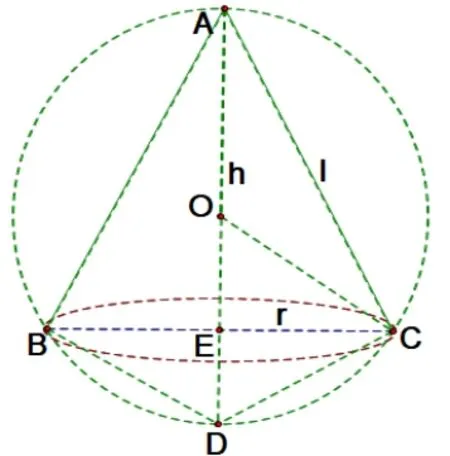
图1-2

对于侧棱相等的棱锥,可作其外接圆锥,如1-1,则此棱锥的外接球和其外接圆锥的外接球是同一个球,设外接球的半径为R,棱锥的侧棱长为l,底面外接圆的半径为r,高为h,则如图1-2,在Rt△ACD中,根据射影定理,可得外接球的半径R满足：

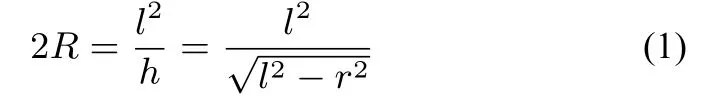
圆锥的外接球问题的表现形式有：

1.圆锥的外接球问题；

2.正棱锥的外接球问题；

3.侧棱相等的锥体的外接球问题；

4.顶点射影为底面外接圆圆心的几何体的外接球问题.

对于这四种外接球问题,都只需找到侧棱即母线的长和底面外接圆的半径,就可用公式(1)解决.

例1(2019年高考全国Ⅰ卷第12 题) 已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2 的正三角形,E、F分别是PA、PB的中点,∠CEF=90o,则球O的体积为( )

图1-3

解析该题显然是正棱锥的外接球问题,根据本位探究法,该题的难点是确定侧棱即母线的长.如图1-3,不妨设侧棱长PA=PB=PC=2a,在边长为2 的正△ABC中,CF=√底面外接圆半径r=在Rt△EFC中,CE2=在△PAC和△AEC中根据余弦定理可得cos ∠PAC=解得侧棱长PC=2a=根据公式(1),三棱锥√P-ABC的半径满足2R=即R=所以外接球的体积为V=

二、长方体的外接球及其表现形式的本位探究

如图2-1,设长方体的长、宽、高分别为a、b、c,长方体的体对角线的交点即为外接球球心,体对角线即外接球的一条直径,可得外接球的半径为R满足：

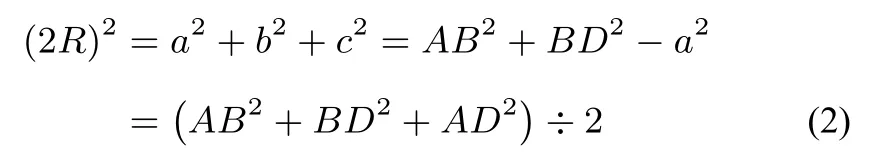
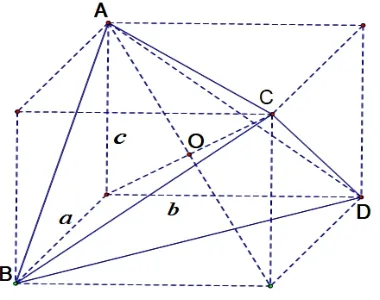
图2-1

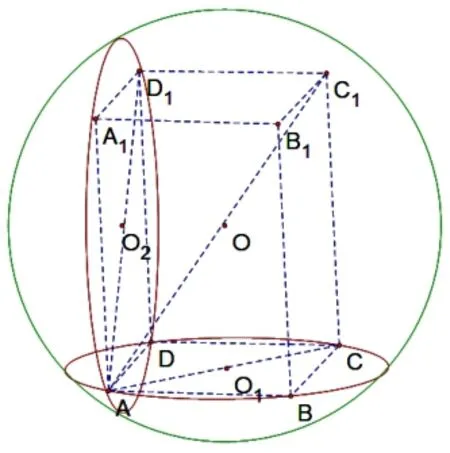
图2-2

引理如图2-2,圆O1和圆O2分别是球O上的两个截面圆,且圆O1和圆O2所在的平面互相垂直,若两圆的半径分别为r1、r2,公共弦为a,则球O的半径R满足：

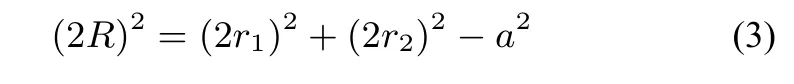
即外接球的直径的平方,等于两个小圆的直径的平方和减去公共棱的平方.

证明如图2-2,从公共棱AD出发分别在圆O1和圆O2做内接矩形,就可以在球O内构造内接长方体ABCD-A1B1C1D1,则该长方体的外接球即球O,根据公式(2) 中第二等式,可得球O的半径R满足(2R)2=(AC)2+(AD1)2-AD2=(2r1)2+(2r2)2-a2.引理得证.

长方体的外接球问题的表现形式有：

1.长方体的外接球问题；

2.三组对棱分别相等的三棱锥的外接球问题；

3.有一个侧棱垂直于底面的几何体的外接球问题；

4.有一个侧面与底面垂直的几何体的外接球问题；

5.顶点射影在底面的边缘的几何体的外接球问题.

表现形式1 可以直接用公式(2)的第一个等式解决；表现形式2,可以补全长方体(见图2-1),用公式(2)的第三个等式解决；表现形式3、4 和5 的本位可以归为长方体外接球问题,根据引理,可用公式(3)解决.此法优点在于不再需要做辅助线,不再需要确切的球心位置,只需找到对应的长方体或两垂面的外接圆即可作答.下面举例说明.

例2某三棱锥三组对棱长相等,分别为求该三棱锥外接球的半径.

解析三组对棱分别相等的三棱锥,符合表现形式2,可以放到长方体中进行求解,如图2-1,由公式(2)的第三等式可得,外接球半径满足(2R)2=(AB2+BD2+AD2)÷2=14,所以该三棱锥外接球的半径为

例3(2019年汕头一模第11 题)三棱锥P-ABC中,PA⊥面ABC,∠ABC=30o,△APC的面积为2,则三棱锥P-ABC的外接球体积的最小值为____.

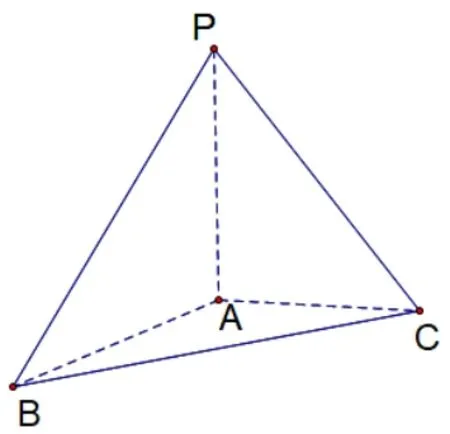
图2-3

解析如图2-3,由条件知PA⊥面ABC符合表现形式3,利用引理作答.设公共棱AC=x,则PA=在△ABC中根据正弦定理得外接圆半径满足2r1==2x,Rt△ACP的外接圆半径满足根据公式(3),三棱锥P-ABC的外接球的半径满足得当且仅当x=时,等号成立.

例4 如图2-4,已知在梯形ABCD中AB//CD,AB⊥AD,AB=2,AC=CD=1,将梯形ABCD沿对角线AC折叠成三棱锥D-ABC,如图2-5,当二面角D-AC-B是直二面角时,三棱锥D-ABC的外接球的体积为_____.

图2-4

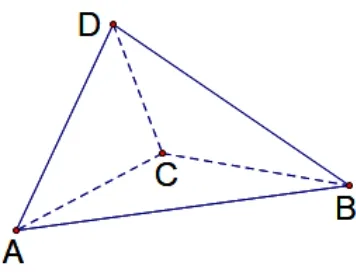
图2-5

解析由条件知面ACD⊥面ABC,符合表现形式4,利用引理作答.易得Rt△ABC的外接圆半径满足2r1=AB=2,Rt△ACD的外接圆半径满足2r2=AC=公共棱为AC=根据公式(3),三棱锥D-ABC的外接球的半径满足(2R)2=(2r1)2+(2r2)2-AC2=4 所以R=1,外接球的体积为

三、菱形折叠的外接球及表现形式的本位探究

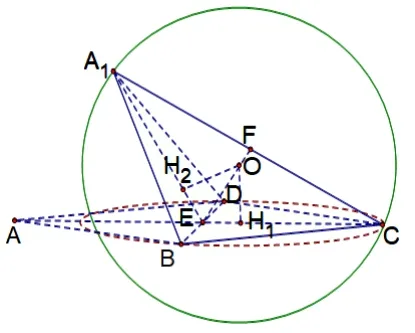
图3-1

如图 3-1,在边长为a的 菱形ABCD中,连AC交BD于E,对角线BD=b,沿BD折成二面角A1-BD-C,A1C=c,取A1C的中点F,三棱锥A1-BCD的外接球的球心必在BD的中垂面A1EC上,且在A1C和BD的公垂线EF上.

第一步：如图3-1,先找出△BCD外心H1；第二步：过H1作面BCD的垂线与EF交点即为球心O,或过H1和H2(△A1BD的外心)分别作BCD和面A1BD的垂线,两垂线的交点即为球心O；第三步：解△OEH1,算出OH1,在Rt△OCH1中,勾股定理OH21+CH21=OC2=R2.[2]

菱形折叠的外接球问题的表现形式有：

1.菱形沿对角线折叠的几何体的外接球问题；

2.两个全等的等边三角形拼在一起的几何体的外接球问题(也可以归于圆锥的外接球问题)；

3.两个全等的等腰三角形拼在一起的几何体的外接球问题.

例5(2019年清华自招题第1 题)一个四面体棱长分别为6,6,6,6,6,9,求外接球的半径.

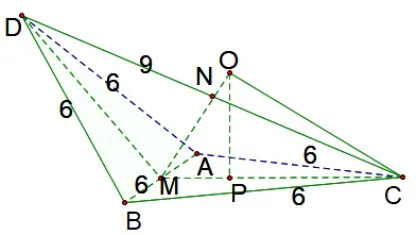
图3-2

解析一如图3-2,在四面体D-ABC中,AB=BC=AC=BD=AD=6,CD=9,可以看成边长为6 的菱形沿对角线折叠而成,符合表现形式1.取AB,CD的中点M,N,易得AB⊥面CDM,MN是AB,CD的公垂线,且面CDM⊥面ABC,等边△ABC的外心P在CM上,过P作PO⊥面ABC,则PO在面CMD中,交MN的延长线于点O,则OA=OB=OC=OD,即O为四面体ABCD的外接球球心.易得MC=MD=6×∠CMD=120o,所以∠NMC=60o,PO=根据勾股定理得OC=即外接球的半径为

解析二换个角度看如图3-2,在四棱锥B-ACD中,侧棱BA=BC=BD=6,可以归为圆锥的外接球问题,在底面△ACD中,sin ∠ACD=,根据正弦定理得,底面外接圆半径满足得根据公式(1),四面体外接球的半径满足即外接球的半径为

四、感悟与反思

对于一般多面体的外接球,都可以建立空间直角坐标系,设球心坐标为(x,y,z),利用球心到各顶点的距离相等建立方程组,解出球心坐标,从而得到球的半径长,此法虽为通性通法,然而实际解题中,建系写坐标及建立方程组求解的过程,存在较大运算量.归根到底,外接球问题意在考察学生的空间想象能力,综合性强、难度大、灵活性强、区分度大.在日常命题与教学中,不应以孤立的刷题为目的,要注重挖掘外接球问题典型题的几何本位,充分展示解题的思维过程,暴露解题思维,多多引导学生提炼解题思维模型,关注通性通法,从“题海战术”中解放,达到以解有穷道题的思维方法获得无穷道题解题方法的成功之道.