由一道初等数学题引发的猜想及其高等证明与推广

合肥市第一中学(230601) 谷留明

在高二下学期讲授导数时,有学生问了这样一个题目：设函数f(x)=(x-a)(x-b)(x-c),a,b,c ∈R 且两两不相等,则

有感于此题解答过程中的美妙的数学形式和对称轮换性,笔者讲解后又追问了该生一个变式思考题：设且两两不相等,则

发现结果也是0.进一步推广到类似的5 次多项式函数,经计算机模拟,结果仍是0.由此提出以下的

猜想设f(x)=(x-a1)(x-a2)···(x-an),a1,a2,···,an ∈R 且两 两不相等,n ∈N 且n ≥3,则

此猜想经教研组同事内部讨论仍未得到证明或者证伪.于是将它张贴到教研组门口的公告板上,面向全校师生进行征解.有两位学竞赛的同学来分享了根据拉格朗日插值公式得到的证明思路.因为知识受限,他们表达得很不清楚严谨,只是感性的一些描述.看来都感觉到了这个看起来简单的初等问题,得寻求高等数学知识来解答.笔者又重新拾起来了高等代数等大学数学知识,得到了以下4 种证明.

下文中,对i=1,2,···,n记

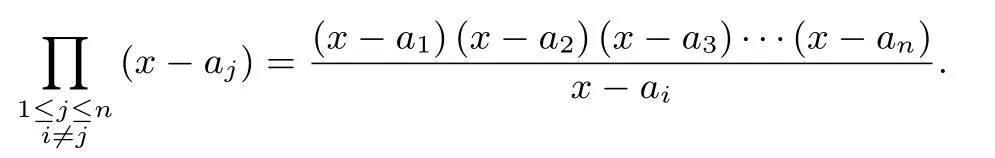
方法1 由得

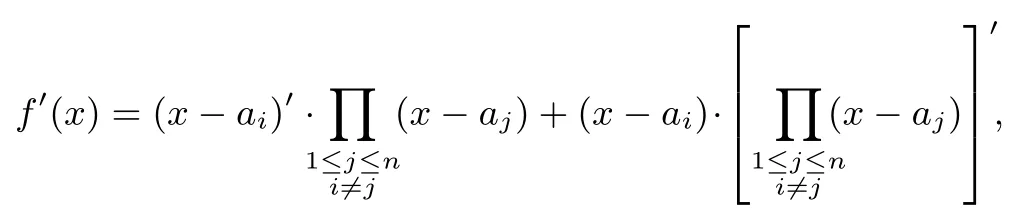
所以

由拉格朗日插值公式得

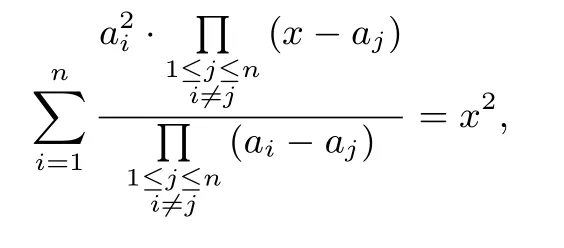
令x=0,得

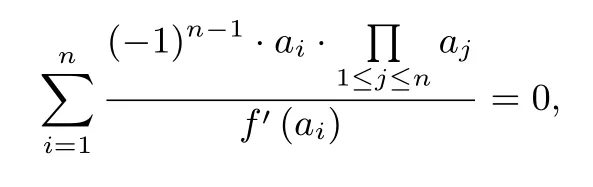
即

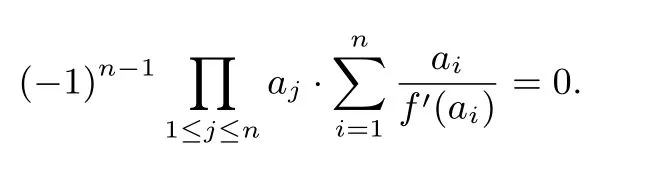
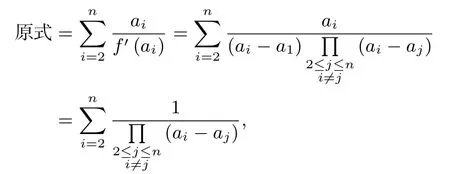
由拉格朗日插值公式,得x=0,得即

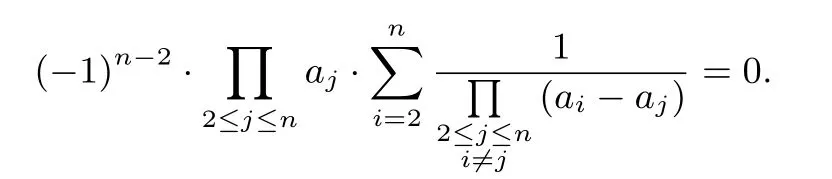
方法2 设则deg(fi(x))=n-1,以R[x]n表示由所有次数不超过n-1的实系数多项式所构成的线性空间,则fi(x)∈R[x]n,可以证明：f1(x),f2(x),···,fn(x) 是R[x]n中的一组基,且因为x ∈R[x]n,所以存在不全为0 的b1,b2,b3,···bn ∈R,使得把x=ai代入,得故又3),故对比xn-1项的系数得即得证.

方法3 由n阶范德蒙德行列式得

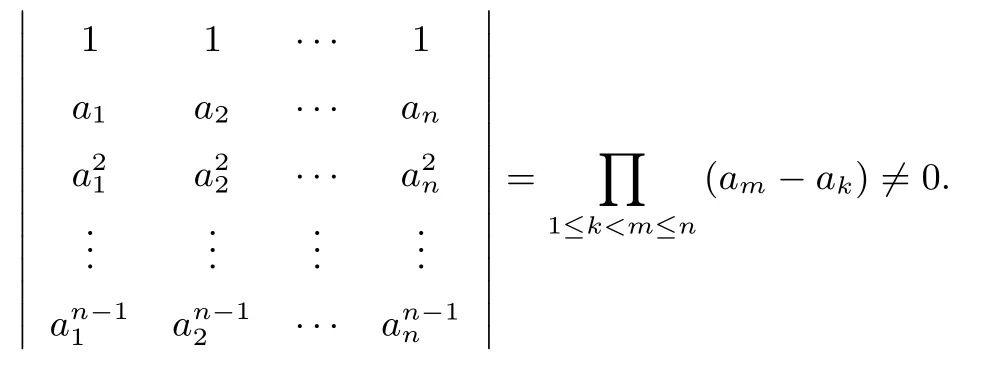
而

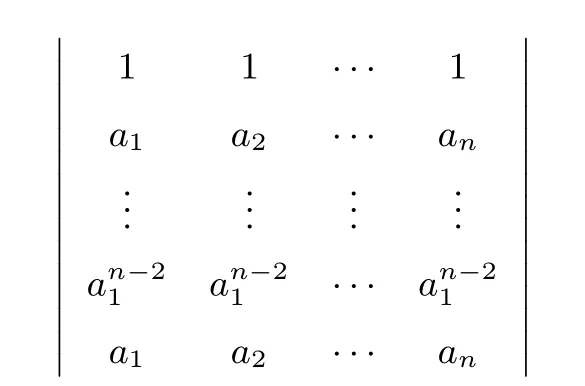
按第n行展开的展开式.因为此行列式的第2、n行相同,所以此行列式的值为0,即

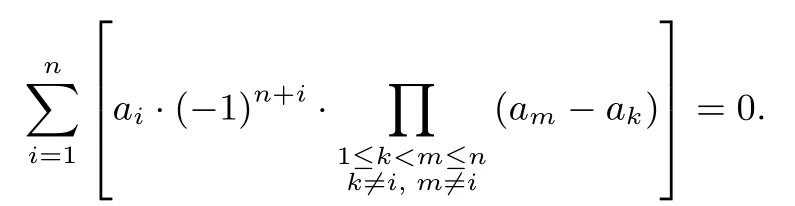
由此证明了上述猜想,这个猜想在结构上,在证明过程中,以及利用作图软件作图探究中,都能感受到对称之美和数学的奇妙.其实中学里,还有类似的题目.例如：设函数f(x)=(x-a)(x-b)(x-c),a,b,c ∈R 且两两不相等,则

其结果也是0.再结合上述证明中的体会和感悟,还可提出以下

猜想2设f(x)=(x-a1)(x-a2)···(x-an),a1,a2,···,an ∈R,且两两不相等,n ∈N,n ≥2,则

用上述三种方法,仍可类似地证明,下面用新的方式来证明.

证明设a1,a2,···,an ∈R且互不相等),则f′n(ai)=由拉格朗日插值公式,存在唯一的次数不超过n-1 的多项式函数

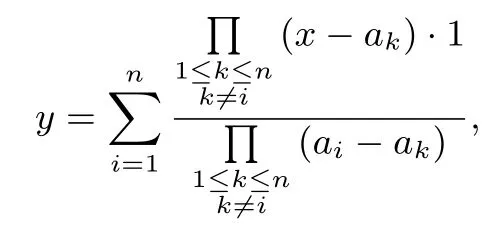
其图像经过平面上的给定的n个点 (a1,1),(a2,1),···,(an,1).而y=1 就是经过这n个点的次数不超过n-1 的多项式函数,所以

即

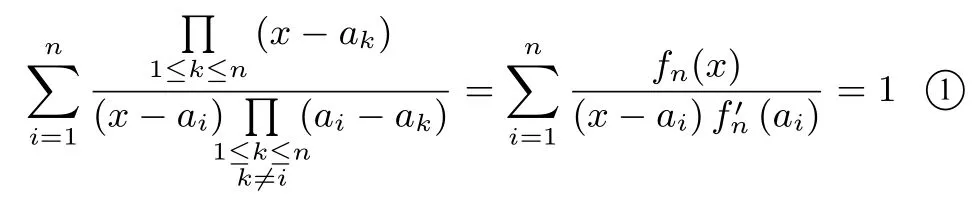
同理,

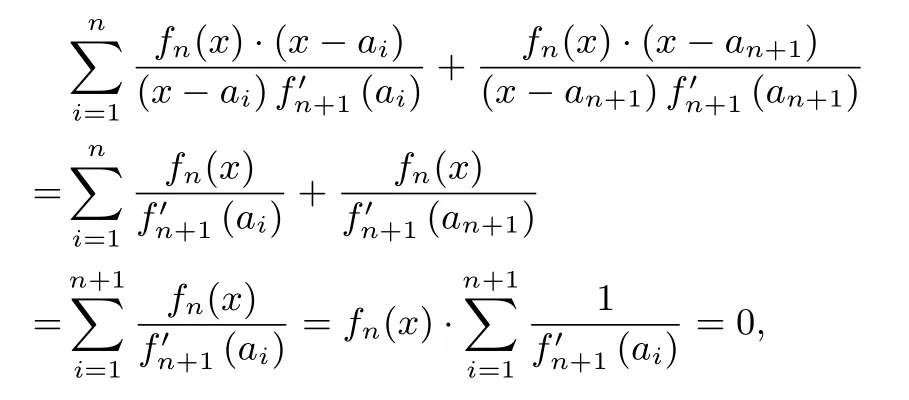
又因为fn(x) 不恒为0,所以有即

由上述两个猜想的结构特征,利用证明猜想1 的方法2和方法3,容易进一步推广,得：

推广设f(x)=(x-a1)(x-a2)···(x-an),a1,a2,···,an ∈R 且两两不相等.当时,恒有

证明(按方法3)因为

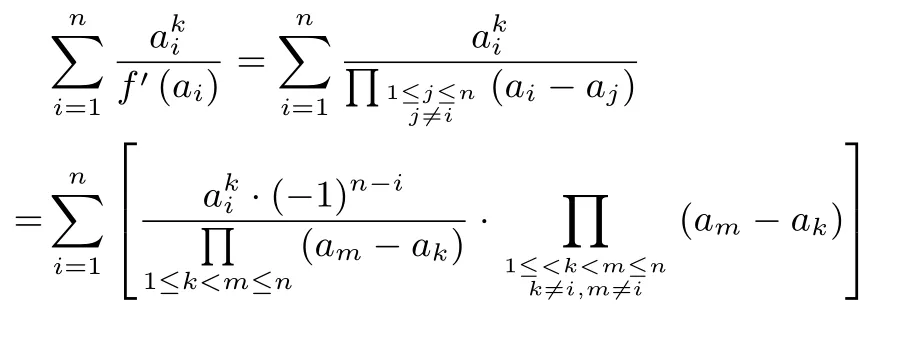
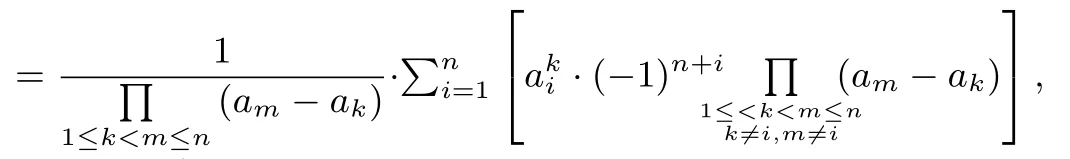
所以当k≤n-2 时,

由这个更一般的结论,很容易命制以下初等题目：

(1) 已知f(x)=(x-a)(x-b),(a,b ∈R 且不等,则

(2)f(x)=(x-a)(x-b)(x-c),a,b,c ∈R 且两两不等,则

(3)f(x)=(x-a)(x-b)(x-c)(x-d),a,b,c,d ∈R且两两不等,则

(4)f(x)=(x-a)(x-b)(x-c)(x-d),a,b,c,d ∈R且两两不等,则

(5)f(x)=(x-a)(x-b)(x-c)(x-d),a,b,c,d ∈R且两两不等,则

这系列题的难点不在导数,换种形式,也可以命制以下证明题.已知a,b,c,d ∈R 且两两不相等,证明：

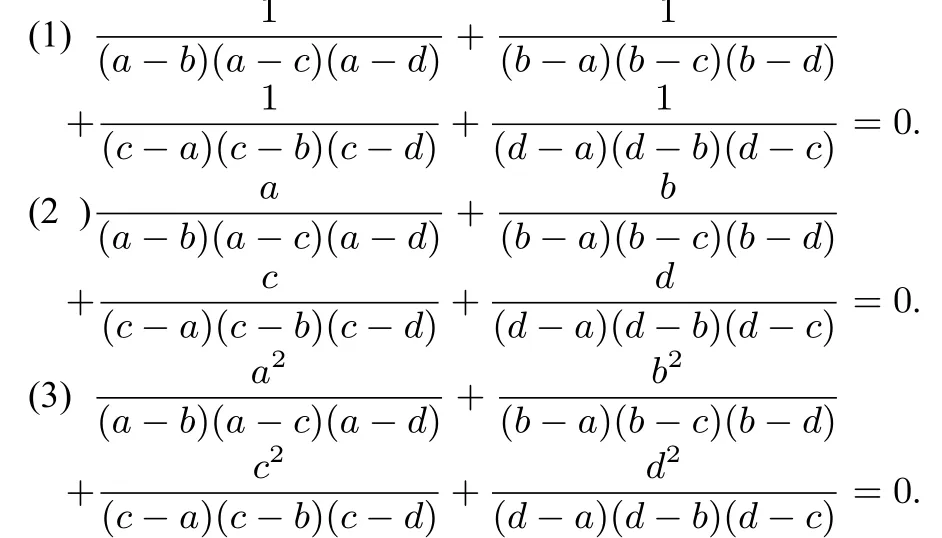
由此,可见教学相长的重要性；教师平时教学中更是要以身作则,坚持举一反三、发散思考；在如今双一流大学更倾向于自主招生的潮流下,面对部分数学优等生,教师远远不能自满,掌握适当的高等数学知识,才能高屋建瓴,给予学生更“高端的指导”.