例谈面面垂直的证明策略
广东省英德中学(513000) 陈国宗
一、概述
立体几何是高中数学的重点内容,也是高考的必考考点之一,问题的考查形式分为位置关系的证明与相关量的计算,其中位置关系的证明会直接或间接地影响相关量的计算,尤其是面面垂直的证明,然而笔者发现学生对面面垂直的证明得分率偏低,原因在于学生对面面垂直的证明理解不够深刻,知其然而不知其所以然,缺乏具体的证明策略.为此,笔者对面面垂直的证明题型进行归纳分类,结合具体实例揭示出证明面面垂直的本质与细节,培养学生直观想象与逻辑推理的数学核心素养.
二、例题分析
类型一公共棱上存在(易作)垂线
例1(2017 全国新课标Ⅲ理科节选) 如图1,四面体ABCD中,△ABC是 正 三角形,△ACD是直角三角形.∠ABD=∠CBD,AB=BD.
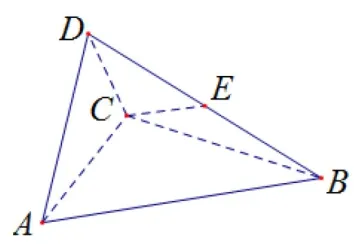
图1
求证:平面ACD⊥平面ABC.
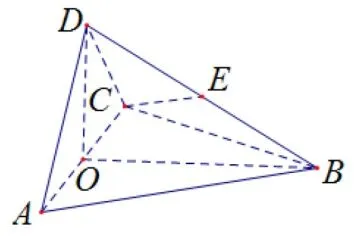
图2
证明取AC中点为O,连接BO,DO,因为△ABC为等边三角形,所以BO⊥AC.令|AB|=a,则|AB|=|AC|=|BD|=a.因为△ACD是直角三角形,故所以|OD|2+|OB|2=|BD|2,由勾股定理的逆定理可得OB⊥OD.因为OD ∩AC=O,所以OB⊥平面ACD,又OB ⊂平面ABC,所以平面ACD⊥平面ABC.
评注对于上述证明过程,笔者曾对学生提出一个问题:你是如何想到去构造辅助线OB,并证明OB⊥平面ACD的? 学生的回答大多是“直观想象”又或者是“只可意会不可言传”,当然笔者并不否定学生直观想象的能力,但担忧在某些情况下可能无法直观想象出来.事实上,从逆推的思想出发,假设平面ACD⊥平面ABC成立,根据面面垂直的性质定理,其中一个平面内垂直公共棱的直线垂直另外一个平面,这就是为什么要构造辅助线OB,并证明OB⊥平面ACD的原因.其本质为面面垂直的判定定理与性质定理之间的逻辑转化.
类型二公共棱上无明显的垂线
例2(2018年深圳一模理科节选) 已知三棱柱ABC-A1B1C1中,底面ABC为边长为的等边三角形,BB1=4 且A1C1⊥BB1,且∠A1B1B=45o.
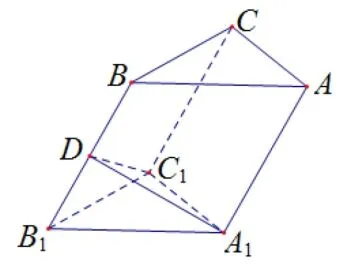
图3
求证:平面BCC1B1⊥平面ABB1A1.
证明作A1D⊥BB1,垂足为D.已知底面ABC是边长为的等边三角形且∠A1B1B=45o,所以A1D=2,因 为A1C1⊥BB1且A1C1∩A1D=A1所以BB1⊥平面A1C1D,故∠B1DC1=90o.又B1A1=B1C1且BD1=BD1,所以△A1B1D∽=△C1B1D,故C1D=A1D=2,所以C1D2+A1D2=A1C21,从而C1D⊥A1D,又C1D ∩BB1=D,所以A1D⊥平面BCC1B1,且A1D ⊂平面ABB1A1,所以平面BCC1B1⊥平面ABB1A1..
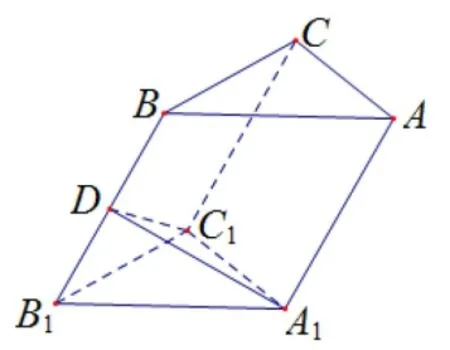
图4
评注本题的特点是两个平面的公共棱上没有明显的垂线,同时也成为了解题的难点.此时可考虑在其中一个平面内向公共棱作垂线且垂足的位置确定,将问题转化为类型一,从而成功地将问题转化为线面垂直的证明.
类型三公共棱上无法作出垂线
引理若α⊥β,n ⊂α,m ⊂β且n⊥m,则n⊥β或m⊥α.
证明①若n⊥β,则结论成立.
②若n不垂直β,如图5所示设α ∩β=l,n ∩l=A,在平面α内以A为垂足作AB⊥l.已知α⊥β,则AB⊥β,又m ⊂β故AB⊥m,又n⊥m,n ∩AB=A且n ⊂α,AB ⊂α,所以m⊥α.
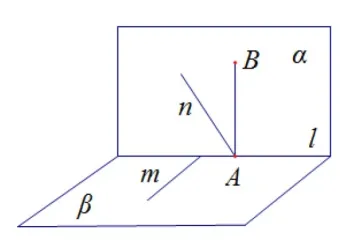
图5
评注该引理可理解为面面垂直性质定理的推广:如果两个平面垂直,则这两个平面内互相垂直的两条直线中至少有一条垂直另外一个平面.该引理为我们在证明面面垂直转化为证明线面垂直时提供了有力依据.
例3在直棱柱ABC=A1B1C1中,AB=AC,BC=CC1,D,E分别是棱BC与CC1的中点.求证:平面ABE⊥平面AB1D.
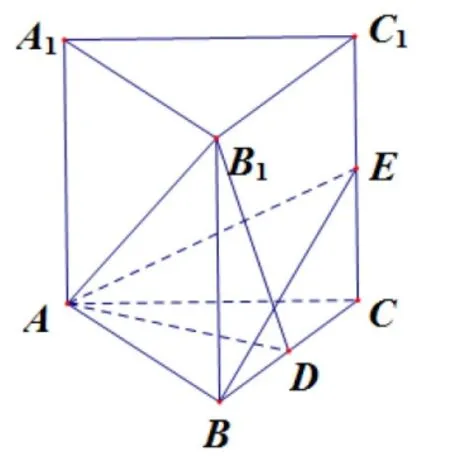
图6
证明在直棱柱ABC-A1B1C1中,B1B⊥平面ABC,AD ⊂平面ABC,所以B1B⊥AD,又AB=AC,D为棱BC中点,BE ⊂平面BCC1B1,所以AD⊥BE,又BC=CC1,故四边形BCC1B1为正方形.所以所以∠BB1D=∠EBC,故∠BB1D+∠B1BE=∠EBD+∠B1BE=90o,所以BE⊥B1D,又AD ∩B1D=D,故BE⊥平面AB1D且BE ⊂平面ABE.所以平面ABE⊥平面AB1D.
评注本题的难点在两平面的公共棱上没有明显的垂线,且不容易在其中某个平面内向公共棱作垂线.分析题目的已知条件,发现这两个平面存在互相垂直的直线即AD⊥BE根据引理,结合几何体的结构特征以及逆推的思想,实现将面面垂直的证明转化为线面的证明即BE⊥平面AB1D.
三、巩固练习
习题1 如图6,四边形ABCD是边长为2 的正方形,E为CD的中点,以AE为折痕把△ADE折起,使点D到达点P的位置,且∠PAB=60o.求证:平面PEC⊥平面PAB.(提示:尝试证明PE⊥平面PAB.)
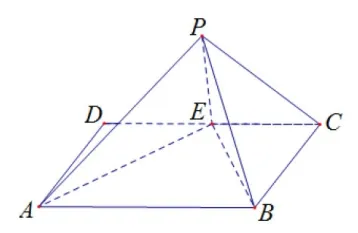
图7
习题2 设D是直角△ABC斜边AC的中点,AB=将△CBD沿着BD翻折,使得点C到达P点位置,且AP=求证:平面PBD⊥平面ABD.(提示:作BD中点O连接OP,尝试证明OP⊥平面ABD.)
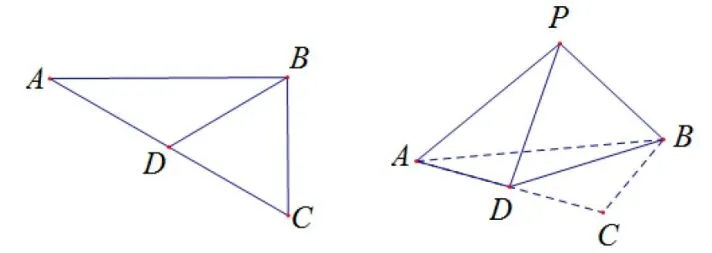
图8
四、结束语
通过本文例题的分析,我们发现证明面面垂直的本质实际上将其转化为证明线面垂直,然而我们教师在面面垂直证明的教学中不能只是简单抽象地概括为转化两个字,还应充分揭示转化的细节,引导学生在不同的情景中归纳出转化的方式,培养学生直观想象的同时发展学生的逻辑推理能力,这样我们的教学才能更进一步地提升学生的数学核心素养.

