伪卫星辅助复杂地形卫星标定方法研究

谢瑞煜，孙瑾

(海军航空大学，山东 烟台 264001)

0 引言

在现代战争中，空袭与反空袭已经成为了一种常见的作战样式。为了提高反空袭能力，防空武器系统有时根据任务需要，需要在一些复杂地形进行部署。在实际部署中，复杂地形特别像峡谷地形虽能有效保护己方设备，但是在用卫星标定时，因为受到地形遮挡，往往标定精度达不到要求。伪卫星作为一种局域增强系统，能有效弥补卫星信号受遮挡的问题，近几年来受到了广泛的关注。

伪卫星是一种基于地面或空中的能够传播类似卫星信号的简易信号发生器。当卫星不能满足定位要求时，可以把伪卫星作为对卫星的补充来进行定位；它通过改善卫星的几何分布，来提高整体定位精度[1-2]。

为了提高战时标定的可用性，文中采用北斗卫星(BDS)进行定位，鉴于目前BDS正在高密度发射期，卫星分布比较差，使用伪卫星能有效提高定位精度。在BDS平台上，目前主要的伪卫星系统有两种模式，分别是伪卫星增强BDS系统和独立伪卫星系统[3-4]。

1 理论基础

1.1 绝对精度因子

在t时刻，对第j颗卫星的测相伪距观测值方程为

(1)

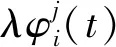
(2)

式中：ΔI为接收机观测噪声；ΔT为卫星观测噪声。

若记A1为设计矩阵，即

(3)

根据最小二乘法则，可得t时刻的协因数阵为

(4)

几何精度因子为

(5)

该系数阵只能用在空间直角坐标系上，对使用纯伪卫星布局时可以使用；如果将伪卫星和BDS卫星进行组合定位，必须将系数阵进行转化，使之能用在站心坐标系上[6]。

转换阵H为

(6)

则基于站心坐标系的协因数阵为

(7)

平面位置精度因子为

(8)

式中：NH=11;EE=22。

1.2 相对精度因子及改进

在实际卫星定位时，定位精度受到电离层和对流层折射影响，卫星高度角越低，影响越大。根据这一特点，在计算精度时可以引入观测值权阵，从而减弱影响。同时为提高定位精度，文中采用双差相对定位法。

目前伪卫星和卫星组合定位的观测值权重确定还没有进行研究，本文提出一种基于高度角的组合定位权阵确定法。伪卫星在布置时，一般与观测站的距离较近，通常是在地面附近，不会受到电离层和对流层折射的影响，文中将系数定位常数1，而卫星部分则将系数设置成与高度角相关[7-8]。观测值权阵为

(9)

式中：ES为组成双差观测值的另一个卫星在观测时段中的平均高度角；EJ为参考卫星J在观测时段中的平均高度角；n为两站同时观测卫星数。

记A2为双差定位的设计矩阵，X为未知数向量，L为常数向量[9-11]，即

(10)

X=(δxi，δyi，δzi，cδti)T.

(11)

误差方程的矩阵形式为

V=AX+L，

(12)

式中：V为残差，根据最小二乘法得

(13)

基于站心坐标系的协因数阵为

(14)

平面位置精度因子为

(15)

2 基于伪卫星的标定方案

在实战背景下，使用伪卫星需要克服几个难点：①伪卫星作为一种新技术，方兴未艾，多布置在城市而不在野外；②防空武器系统在不同的地形部署时，为了达到标定精度，伪卫星的布局需要优化；③为了提高布置效率，需要用最少的伪卫星来满足定位精度。

2.1 方案设计

根据部署地地形地貌和可观测到的BDS卫星数量，本文将其分为3类：第1类，部署地四周及天空无遮挡，可观测到的卫星数量平均在8颗以上，这种称之为开阔地形；第2类，部署地四周及天空部分遮挡，可观测到的卫星数量平均在4～7颗，这种称之为半开阔地形；第3类，部署地四周及天空严重遮挡，可观测到的卫星数量平均在3颗以下，这种称之为峡谷地形。

防空武器系统在标定时，第1步对该地形进行简单测绘，搜索可用的卫星数量，第2步布置一定数量的移动伪卫星，第3步优化伪卫星布局，第4步通过计算并判断精度因子(DOP)大小，当DOP小于3时，伪卫星部署完成；若DOP大于3时，则继续添加1颗伪卫星，重复上述步骤，直至DOP符合要求。流程图如图1所示。

2.2 快速布置方案

根据2.1节设计方案，如果每次防空武器系统变换部署阵地后，伪卫星都要重新布置，这将会严重影响标定的效率。本文提出将多种典型地形事先进行伪卫星布局实验，经过2.1节的流程，得出一系列典型地形的布局预案，供下次部署时参考应用。有了这些预案，标定前步骤为先测绘部署地的地形，并寻找与之相类似的布局预案，根据预案添加伪卫星并直接布局。这过程中省去了寻找最优布局的环节，节省时间并减少工作量，能使标定效率大大提高。流程图如图2所示。

图1 伪卫星布置流程图Fig.1 Pseudo satellite layout flow chart

图2 快速标定流程图Fig.2 Quick calibration flow chart

3 仿真分析

为了确定不同地形所采用的伪卫星布局方案，本文通过仿真运算，模拟几个典型地形，来得出相应的伪卫星最优布局。由于第1类开阔地形不受到遮挡，不需要伪卫星，这里不再进行仿真。

3.1 模拟第2类半开阔地形

该地形中防空武器系统部署在长10 km，宽1 km，坡顶到坡底水平距离为0.1 km的地形中。如图3所示。

图3 半开阔地形部署图Fig.3 Semi-open terrain deployment map

如图3建立空间直角坐标系，五角星代表指挥单元，坐标为(5,0.5,0) km，三角形代表武器单元，坐标分别是(3,0.1,0) km，(3,0.9,0) km，(7,0.1,0) km，(7,0.9,0) km。斜坡设置成3种不同的坡度，分别为45°，60°和75°。

在这一地形中，可观测到的卫星较多，一天中的数量如图4所示。

考虑到BDS还未发射完成，文中采用Matlab仿真GPS卫星运行[12]，在(6 400,0,0) km这一站心坐标系坐标位置，图4是坡度分别是45°，60°，75°时观测到的卫星数量。这里采用伪卫星和卫星组合差分相对定位的方法。

图4 3种坡度的可见卫星数目Fig.4 Number of visible satellites on three slopes

3种坡度的伪卫星采取的布置坐标相同，在图3空间直角坐标系中布置时，添加1颗星坐标为(5,-0.1,0.1) km；添加2颗星坐标为(0,-0.1,0.1) km，(5,-0.1,0.1) km；添加3颗星坐标为(5,-0.1,0.1) km,(0,0,0) km，(10,0,0) km。

它们的HDOP变化情况如图5～7所示。

图5 45°坡HDOP变化情况Fig.5 HDOP changes at 45° slope

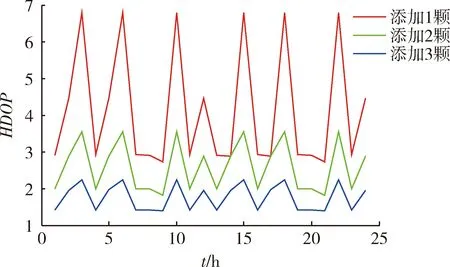
图6 60°坡HDOP变化情况Fig.6 HDOP changes at 60° slope

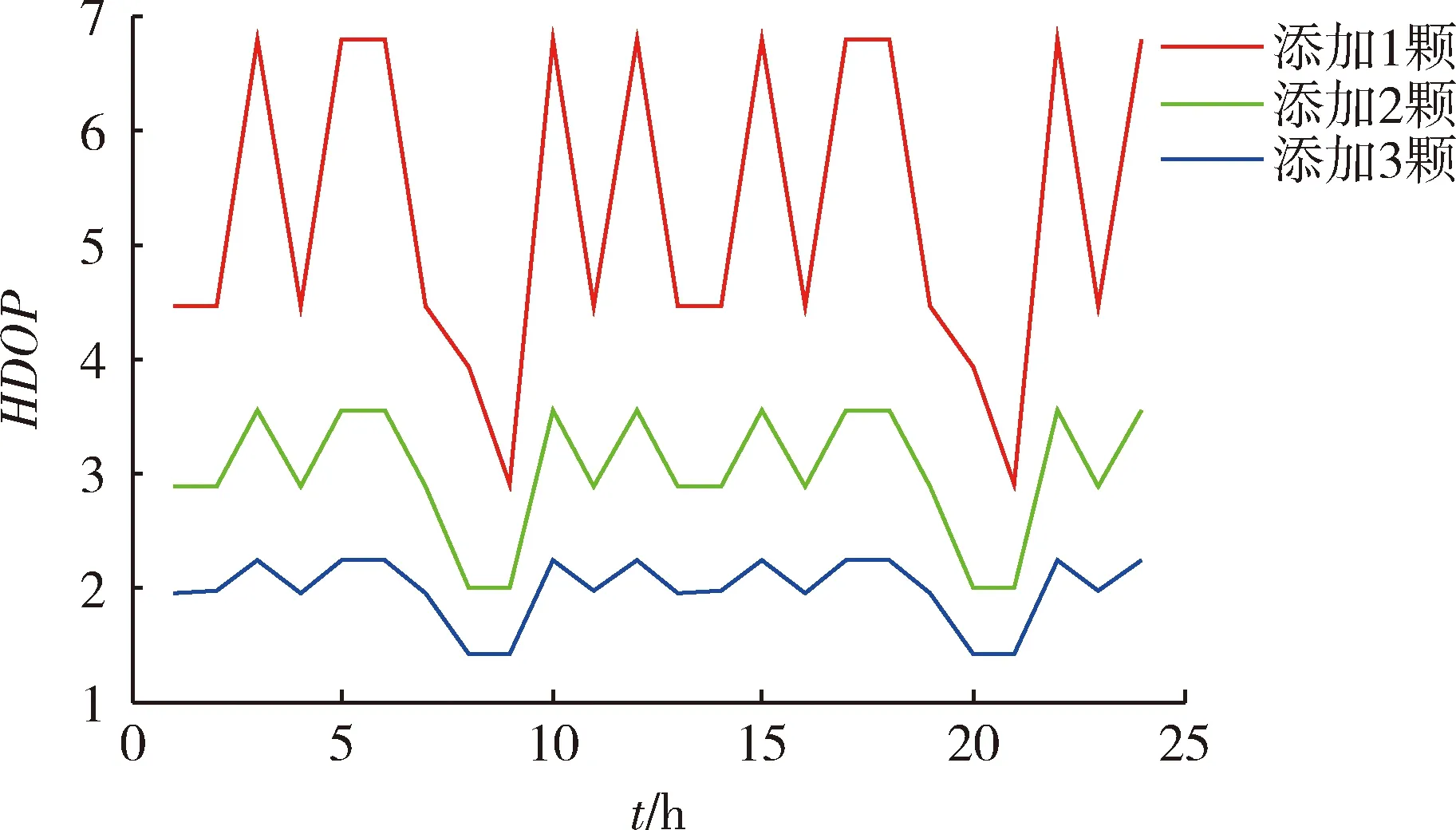
图7 75°坡HDOP变化情况Fig.7 HDOP changes at 75° slope

图5中添加1颗星HDOP 24 h平均值为2.943 7，添加2颗星HDOP 24 h平均值为1.981 6，添加3颗星HDOP 24 h平均值为1.438 5。

图6中添加1颗星HDOP 24 h平均值为4.118 7，添加2颗星HDOP 24 h平均值为2.584 7，添加3颗星HDOP 24 h平均值为1.747 8。

图7中添加1颗星HDOP 24 h平均值为5.250 9，添加2颗星HDOP 24 h平均值为3.109 4，添加3颗星HDOP 24 h平均值为1.979 7。

按照DOP小于3才可以标定的原则，45°坡时添加1颗，2颗，3颗都可以满足要求，但考虑到布置时间及布置成本的因素，选择1颗星布置为佳；同样方法，60°时选择2颗星布置为佳；75°时选择3颗星布置为佳。

3.2 模拟第3类峡谷地形

该地形中防空武器系统部署在长10 km，宽1 km，坡顶到坡底水平距离为0.1 km的地形中。如图8所示。

图8 峡谷地形部署图Fig.8 Canyon terrain deployment map

如图8建立空间直角坐标系，武器系统部署坐标和坡度设置与图3一致。

在这种地形中由于观测到的卫星很少，一天中数量在0～3颗变化，考虑到卫星数量少，而且组合定位影响因素较多，这里采用基于伪距绝对定位的纯伪卫星布局法[13-14]。每种坡度的伪卫星布置数量分别采用4颗，5颗，6颗，考虑到伪卫星布置在坡底影响武器部署，使它只能布置在坡上；布局位置采用粒子群算法进行优化，粒子种群数为100，迭代次数为300，适应值函数为指挥单元和武器单元GDOP的平均值[15-16]。

经算法优化计算，斜坡为45°时，4颗星的布置坐标为(0,0,0) km，(5,0.5,0) km，(10,0,0) km，(5,1.1,0.1) km；5颗星的布置坐标为(0,0,0)，(5,0.5,0)，(10,0,0) km，(5,1.1,0.1) km，(5,-0.1,0.1) km；6颗星的布置坐标为(0,0,0) km，(0,1,0) km，(10,0,0) km，(10,1,0) km，(5,-0.1,0.1) km，(5,1.1,0.1) km。

斜坡为60°时，4颗星的布置坐标为(0,0,0) km，(5,0.5,0) km，(10,0,0) km，(5,1.1，0.173 2) km；5颗星的布置坐标为(0,0,0) km，(5,0.5,0) km，(10,0,0) km，(5,1.1,0.173 2) km，(5,-0.1,0.173 2) km；6颗星的布置坐标为(0,0,0) km，(0,1,0) km，(10,0,0) km，(10,1,0) km，(5,-0.1,0.173 2) km，(5,1.1,0.173 2) km。

斜坡为75°时，4颗星的布置坐标为(0,0,0) km，(5,0.5,0) km，(10,0,0) km，(5,1.1,0.373 2) km；5颗星的布置坐标为(0,0,0) km，(5,0.5,0) km，(10,0,0) km，(5,1.1,0.373 2) km，(5,-0.1,0.373 2) km；6颗星的布置坐标为(0,0,0) km，(0,1,0) km，(10,0,0) km，(10,1,0) km，(5,-0.1,0.373 2) km，(5,1.1,0.373 2) km。

3种坡度的GDOP进化曲线如图9～11所示。

图9 45°角GDOP进化曲线Fig.9 45° GDOP evolution curve

图10 60°角GDOP进化曲线Fig.10 60° GDOP evolution curve

图9中4颗星GDOP收敛值为2.968 1，5颗星GDOP收敛值为2.547 4，6颗星GDOP收敛值为2.271 6。图10中4颗星GDOP收敛值为3.331 5，5颗星GDOP收敛值为2.664 5，6颗星GDOP收敛值为2.374 5。图11中4颗星收敛值为3.998 3，5颗星收敛值为3.067 4，6颗星收敛值为2.516 5。

武器系统在谷底布置时，如果布置位置变更，需要重新计算该布置点坐标的GDOP值。为了减轻工作量依据不同坡度的最佳伪卫星布置方案，用三维曲面图来表示GDOP值，如图12是75°角6颗伪卫星GDOP分布图，可以直观地知道该坐标点的GDOP值，省去重新计算时间。

通过仿真计算，采用2.1伪卫星数量选择法，45°坡时选择4颗星布置为佳；60°时选择5颗星布置为佳；75°时选择6颗星布置为佳。通过仿真可以得出可观测卫星数，地形地貌，需要布置伪卫星数量之间的关系，如表1所示。

图11 75°角GDOP进化曲线Fig.11 75° GDOP evolution curve

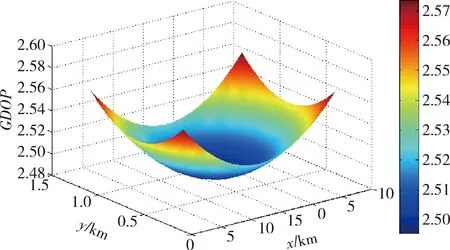
图12 75° 6颗伪卫星峡谷谷底GDOP分布图Fig.12 GDOP distribution of the bottom of 6pseudo-satellite valleys at 75°

类型第1类第2类第3类地貌无遮挡部分遮挡遮挡严重可观测卫星[8,+∞][4,7][0,3]应添加伪卫星0[1,3][4,6]

4 结束语

针对复杂地形标定精度的问题，本文根据不同地形特点和可观测的卫星数量，提出了基于伪卫星增强BDS定位的方案.该方案有效解决了复杂地形因信号遮挡带来的标定精度不高的问题，通过模拟不同的地形地貌，得出不同地形下采取的伪卫星布局方案，在部署时可以缩减伪卫星布置时间，减少工作量，提高标定效率。同时，本文提出了加入观测值权阵来提高BDS和伪卫星组合相对定位精度的方法，但是本文没有进行验证试验，这一项工作有待于进一步的研究。