无人直升机航路跟踪控制系统设计与仿真

孙岭，吴超，周伟，王珂

(1.空军装备部驻景德镇地区军事代表室，江西 景德镇 333002；2.陆军航空兵学院，北京 101123；3.中国陆军航空兵部队兰州代表处，甘肃 兰州 730070)

0 引言

无人直升机是一个多输入/多输出的强耦合非线性欠驱动系统。在设计其飞行控制系统时，被控对象模型的建模误差难以完全消除，建模精度将直接影响控制效果；且无人直升机在悬停和小速度时由于存在纵向长周期发散模态，受扰后(质量变化、惯量变化和风)直升机运动将出现发散运动。因此，无人直升机航路跟踪飞行控制系统需具备良好的鲁棒性和抗干扰性。

典型无人直升机航路跟踪飞行控制系统由内至外常分为角速率增稳、姿态控制和航路控制(速度和位置)3个层级。角速率增稳起到内回路阻尼增稳的作用；姿态控制是速度和航路控制的基础必须拥有良好的姿态控制能力，即具备一定的解耦性和鲁棒性；航路控制回路(常规飞行科目)尽可能消除侧滑角，同时还须具备良好的鲁棒性。

基于线化的状态空间方程，文献[1-2]通过经典PD控制，实现无人直升机姿态解耦控制。基于“一拍”实现跟踪控制的假设，文献[3-4]设计了矩阵形式的显模型跟踪姿态控制内回路，文献[5]则基于该回路搭建了速度和位置控制回路。基于H∞控制理论，文献[6-8]将Raptor-90内回路的特征根配置到理想位置，设计了具有一级飞行品质的内回路姿态控制系统，并应用完全跟踪控制技术实现了突风下的空间航路控制。然而这些算法依赖于被控对象的建模精度，或是针对单一扰动进行设计和验证[9]。

基于定常旋翼挥舞动力学方程，文献[10-11]基于受模型精度影响较小、鲁棒性较强的增量非线性动态逆控制算法，搭建了有人直升机多回路控制系统，实现了对速度的跟踪控制。通过引入一阶命令预测滤波器，文献[12]在固定翼无人机上采用增量动态逆控制方法实现了姿态控制。然而该算法并没有实现完整的航路跟踪控制。

鉴于此，本文在非线性飞行动力学模型的基础上，搭建无人直升机的三回路姿态控制器，内回路和中间回路分别基于扩展非线性动态逆实现对三轴角速率和姿态角的控制，外回路基于PI控制器实现对航迹和空速的控制[13]，基于扩展非线性动态逆实现对垂向速度和高度的控制。

1 飞行动力学模型

1.1 全机动力学和运动学方程

力和力矩方程：

(1)

(2)

式中：V=(u,v,w)T为线速度；W=(p,q,r)T为角速度；F为合外力(包括重力);M为外力矩;I为全机惯性矩阵;Ω为叉乘向量算子，定义如下：

欧拉运动和导航方程为

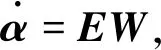
(3)

(4)

1.2 旋翼挥舞动力学方程[14]

(5)

式中：τe为带稳定杆的等效旋翼时间常数；uw,vw和ww分别为风在机体坐标系下3轴的速度；δlon,δlat和δcol分别为纵、横向和总距操纵输入；Alon和Blat分别为周期变距到桨叶挥舞角的增益系数；λ和μ分别为前进比和入流比；a1和b1分别为一阶纵向和横向挥舞角；aMR和σMR分别为主旋翼升力线斜率和桨盘实度；Kμ为速度到桨叶挥舞角的增益系数；Ω和R分别为旋翼转速和旋翼半径。

1.3 合外力和合外力矩

合外力包含气动力和重力2部分，合外力矩由气动力矩产生。气动力分为旋翼、尾桨、尾翼和机身4部分进行计算。

旋翼和尾桨均基于叶素理论计算气动载荷：

(6)

式中：FMR和MMR为旋翼气动力和气动力矩;FTR和MTR为尾桨气动力和气动力矩。

平尾和垂尾产生的升力和阻力为

(7)

式中：qHS和qVF为平尾和垂尾动压；SHS和SVF为平尾和垂尾面积；CLHS和CLVF为平尾和垂尾升力系数；CDHS和CDVF为平尾和垂尾阻力系数。

由式(6)可计算出尾翼合力FEM和合力矩MEM。

机身产生的气动力Ffus为

(8)

式中：ρ为大气密度；Sx，Sy和Sz为机体轴3个方向的有效阻力面积；ua，va和wa为3轴空速分量；vimr和vfus为旋翼诱导速度和机身气动中心合速度。

全机重力投影到机体坐标系下得FG。

综上，式(1)～(5)构成了非线性状态方程组

(9)

式中:U=(δcol,δlon,δlat,δTR)T,X=(V,W,α,P,a1,b1)T分别为操纵输入和状态量。

2 增量非线性动态逆控制原理

一个多输入/多输出系统的状态空间方程为

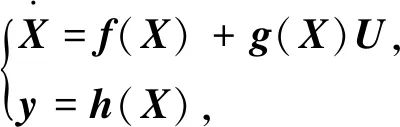
(10)

式中：X,U和y分别为状态量、输入量和输出量。

考虑模型扰动，式(10)可写为

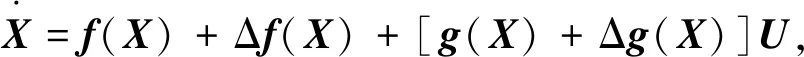
(11)

式中：Δf(X)和Δg(X)为模型扰动。

常规非线性动态逆的控制律为

u=g-1(X)[v-f(X)],

(12)

式中：v为虚拟控制量。

将式(12)带入式(11)可得

[In×n+Δg(X)g-1(X)]v.

(13)

式(10)状态方程作一阶泰勒级数展开，可得

g(X0)(U-U0)，

(14)

当系统采样时间足够小时，X-X0的变化可以忽略，式(14)可化简为

(15)

增量非线性动态逆控制律即为

(16)

由式(16)的控制律可看出增量非线性动态逆控制的优点，无需知道∂fi(X,U)/∂X，而常规非线性动态逆控制必须获知与状态量直接相关部分的模型，而该模型的估计和计算精度依赖于建模精度。

考虑模型扰动，式(15)可变为

(17)

将式(16)带入式(17)得

(18)

式中：C=Δg(X0)g-1(X0)。

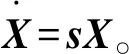
sX=-sCX+(In×n+C)K(Xr-X).

(19)

对于第i个通道，被控量(状态量)与参考量的传递函数为

(20)

采用简单的控制器通道间仍可以取得较好的解耦控制控制效果，且系统的稳定性可得到保证(特征根为s=-Ki(s))。

3 航路跟踪控制系统的设计

3.1 角速率控制内回路

为了方便表述，上文采用式(10)形式的方程进行增量非线性动态逆控制原理的分析(分为f(X)和g(X)2部分)，而直升机飞行动力学方程组为式(9)形式(两者耦合在一起)，因此下文针对式(9)形式的方程进行控制律设计和计算。

对式(2)进行泰勒级数展开(保留到一阶)：

(21)

(22)

无人直升机滚转、俯仰和航向运动是分别通过δlat，δlon和δTR进行控制，总距操纵δcol保持配平值不变，无需计算对总距的偏导数。本文采用中心差分法在线数值计算3×3的偏导数矩阵Brot。

由式(22)可得到控制量的表达式为

(23)

式中：v为内回路虚拟控制量。

系统输入输出变为一阶线性化系统，为了控制输出跟踪参考输入信号的速度，引入反馈增益对角矩阵K1。基于增量动态逆的角速率内回路控制系统如图1所示。虚拟控制量v的计算式为

v=K1(Wr-W0)，

(24)

式中：Wr为角速度参考信号。

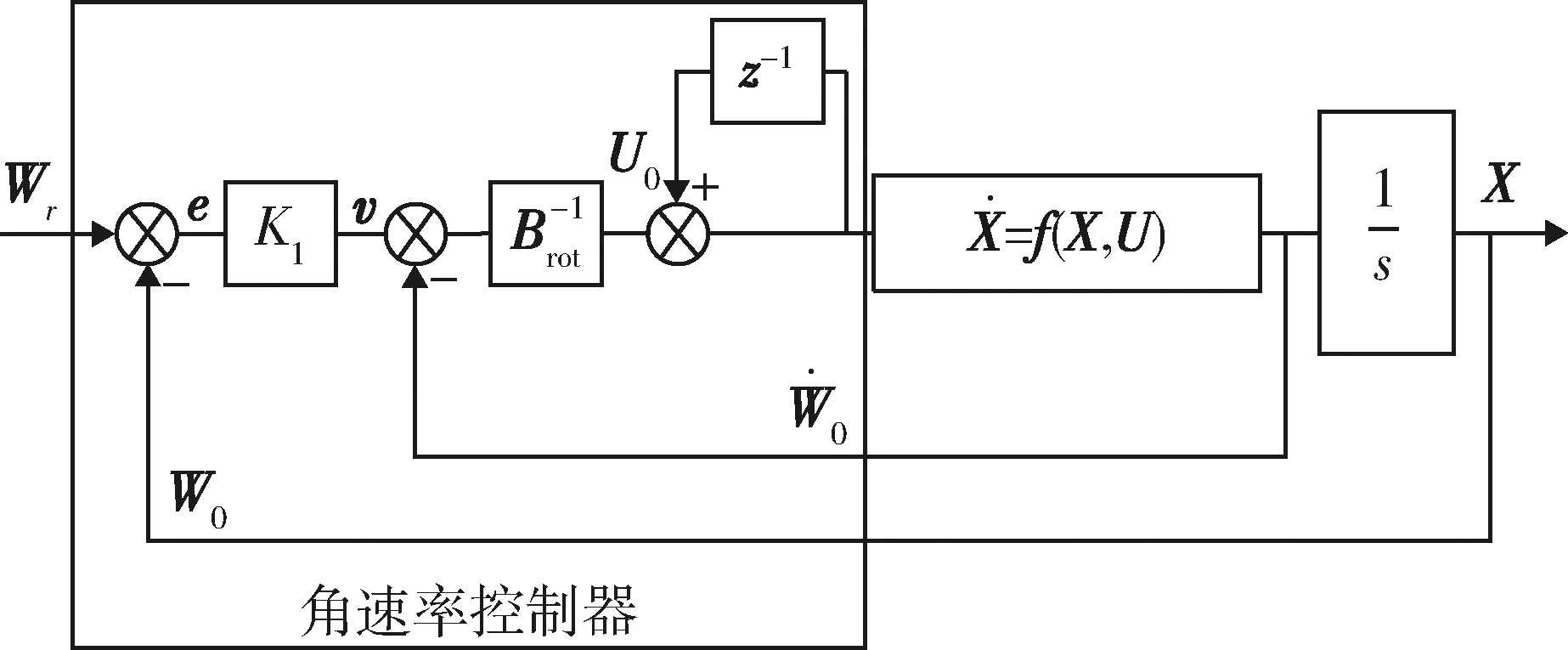
图1 角速率控制回路Fig.1 Angular rate control loop

3.2 姿态控制内回路

由式(3)可得到如下表达式：

(25)

为外回路虚拟控制量。为了控制姿态响应跟踪参考信号的速度，引入反馈增益对角矩阵K2。基于增量动态逆的姿态回路如图2所示。虚拟控制量vα的计算式为

vα=K2(αr-α0).

(26)

图2 姿态控制回路Fig.2 Attitude control loop

3.3 航路控制回路

3.3.1 航迹角控制

航迹角χ计算公式为

χ=atan2(Vy,Vx),

(27)

式中：Vx，Vy为北向和东向速度。

航迹角控制结构如图3所示。一方面航迹控制指令通过PI控制器生成滚转角指令信号，通过滚转角(图1)和滚转角速率控制器(图2)后控制直升机滚转，使旋翼拉力矢量存在一个侧向分量，直升机的投影将在做曲线运动，实现对外回路航迹角的控制；另一方面航迹控制指令直接作为偏航角的控制指令，使偏航角去跟踪航迹角从而控制侧滑角β=χ-ψ=0，实现协调转弯。

图3 航迹角控制回路Fig.3 Course angle control loop

3.3.2 空速控制

速度控制指令通过PI控制器生成俯仰角控制指令，经过俯仰角(图1)和俯仰角速率(图2)控制器实现对速度的控制，参见图4所示。

图4 空速控制回路Fig.4 Airspeed control loop

3.3.3 高度控制

(1) 垂向速度控制内回路

由式(3)可得

(28)

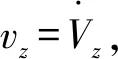
(29)

总距控制量计算表达式为

(30)

式中：δcol,0为当前时刻总距，Bcol定义为

与角速率控制内回路类似(图1)，基于增量动态逆的垂向速度控制回路如图5所示。

(2) 高度控制外回路

定义虚拟控制量vh为

(31)

基于增量动态逆的高度控制回路如图6所示。

图5 垂向速度控制回路Fig.5 Vertical velocity control loop

图6 高度控制回路Fig.6 Altitude control loop

4 仿真验证

4.1 角速率跟踪

3个通道同时给定幅值为5(°)/s的双峰参考信号，如图7所示。选取增益矩阵K1=diag(8,8,10)，其响应和控制输入如图8和图9所示。

图7 双突峰角速率参考指令信号Fig.7 Doublet angular rate reference signals

图8 角速率响应Fig.8 Angular rate responses

图9 操纵输入Fig.9 Control inputs

图10 双突峰姿态参考指令信号Fig.10 Doublet attitude reference signals

3个通道均能较好地跟踪双峰指令信号，在双峰阶跃点附近三轴角速率均有较小的振荡现象，这是由于偏导数矩阵Brot的数值误差带来的。

4.2 姿态跟踪

3个通道同时给定幅值为5°的双峰参考信号，如图10所示。选取增益矩阵K2=diag(2,2,2)，姿态响应如图11所示，角速率响应和控制输入如图12和图13所示。

图11 姿态响应Fig.11 Attitude responses

图12 角速率响应Fig.12 Angular rate responses

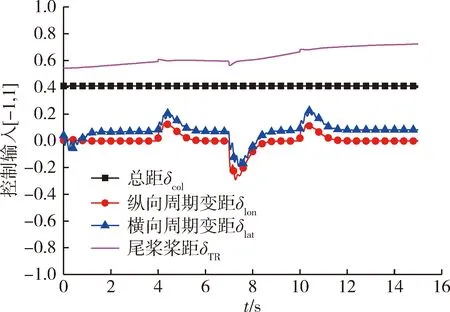
图13 操纵输入Fig.13 Control inputs

3个通道均能较好地跟踪双峰指令信号，滚转角和俯仰角0时刻为配平值，1 s后跟踪上0姿态角的指令，0～1 s俯仰角速率较大，角速率和控制输入均在双峰阶跃点附近有突峰现象。

4.3 航路跟踪

算例直升机0 s时刻在10 m高开始朝正北飞行，其航路点如表1所示，空速参考指令为Vc=3 m/s。算例直升机在以下4种工况进行综合仿真：

(1) 无扰动；

(2) 叠加图14中的1-cos(·)突风扰动[15]，机体坐标系下x,y和z轴的峰值均为5 m/s；

表1 航路点Table 1 Waypoints

(3) 2中的突风扰动+质量m(-0.2m)扰动+惯性矩扰动I(-0.2I)；

(4) 2中的突风扰动+质量m(+0.2m)扰动+惯性矩扰动I(+0.2I)。

算例直升机的状态响应参见图15。

图14 突风扰动Fig.14 Gust wind

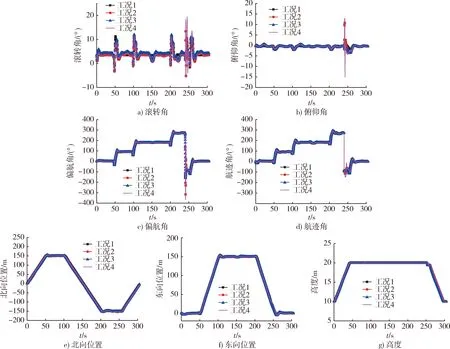
图15 算例直升机响应曲线Fig.15 Example helicopter response curves

由图15可以看出4种工况下算例直升机的状态量几乎完全相同，本文搭建的控制器具有较好的鲁棒性和综合抗扰效果(外部扰动：风，内部扰动：质量和惯性矩扰动)。图16为导航平面2D图，可以看出本文搭建的控制器在4种工况下均能较好跟踪矩形的航迹，过渡较为平滑。图17为飞行轨迹3D图，由图17可以看出4种工况下算例直升机均能较好地跟踪参考航路，实现直升机的“五边飞行”科目。图18为对应的操纵量，操纵量也均在物理可实现的范围之内。

图16 2D导航平面航迹Fig.16 2D Navigation plane flight path

图17 3D飞行轨迹Fig.17 3D flight path

图18 操纵输入Fig.18 Control inputs

5 结束语

基于增量非线性动态逆实现了内回路角速率和中间回路姿态角的跟踪控制，外回路航迹和空速控制则采用PI控制器跟踪指令信号，而高度控制仍基于增量非线性动态逆实现垂向速度和高度控制，由此搭建了无人直升机航路跟踪控制系统。通过4种工况下的飞行仿真表明该系统合理有效，能较好地实现对航路的跟踪控制，且具有良好的鲁棒性和综合抗扰效果。