多谐差相信号激励下的频率特性测试方法研究

宿常鹏，王雪梅，许哲，李骏霄，王迪

(1.火箭军工程大学，陕西 西安 710025；2.火箭军士官学校，山东 青州 262500)

0 引言

伺服机构作为导弹控制系统的执行机构，其动态性能直接影响了导弹飞行控制的精度。频率特性作为衡量动态性能的重要指标，是伺服机构测试的重要内容。目前，伺服机构的频率特性测试仍采用传统的正弦相关分析法，该方法虽然测试精度高，但是测试速度慢、测试效率低的问题十分突出。

近年来，在频率特性的快速测试方面已经取得了许多进展，如文献[1]提出了一种基于调频脉冲扫频信号的频率特性测试方法，可在起始频率和终止频率按线性或指数方式充分激励系统，提高了测试速度和测试效率，但对干扰信号敏感。文献[2]提出了基于伪随机信号相关辨识的测试方法，能够实现频率特性的在线测试，但可重复性差，测试精度不高。文献[3]提出了以多频声信号为激励信号，采用相关分析法进行数据处理的频率特性测试方法，该方法明显缩短了测试时间，但是信号波动程度大影响测试精度。文献[4]研究了以多谐差相信号为激励信号，采用最小二乘法进行数据处理的频率特性测试方法，显著提高了测试精度和速度，但求解过程中容易遇到数字病态问题。

本文从激励信号和数据处理算法2个方面对多谐差相信号测试法进行了改进。首先，提出了功率调制和相位修正2种方法降低多谐差相信号的峰值因子。其次，通过采用镜像映射法进行数据处理，有效避免了方程求解的数字病态问题。最后，以某型导弹的伺服机构为测试对象，分别在无噪声和有噪声的条件下进行仿真，对比正弦相关分析法的测试结果，验证了改进方法的有效性。

1 多谐差相信号研究

Schroeder M.R[5]于1970年提出了多谐差相信号(Schroeder phased harmonic signal，SPHS)的概念。它是一种由若干个功率、周期和初相有一定关系的余弦波叠加而成的多频信号。其表达式为

(1)

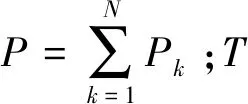
多谐差相信号采用Schroeder相位编码准则调整各余弦分量初相，以降低信号的峰值因子，表达式为

(2)

(3)

在许多应用中，相角必须限制为0和π，这对应于在时间上对称的波形。将相位编码公式舍入到π的整数倍后，式(2)简化为

(4)

式中：[*]表示向0取整运算。

对于均匀功率谱信号，式(3)可简化为

(5)

作为衡量信号波动幅度大小和激励是否均匀平稳的标准[6]，峰值因子的定义为

(6)

以参数为N=16，T=0.5 s，P=1 W的多谐差相信号为例，均匀功率谱的多谐差相信号峰值因子为1.89，其波形如图1所示。若对谐波功率采用正弦调制方式产生非均匀功率谱信号，信号的峰值因子降为1.64。正弦调制的通式为

(7)

若在均匀功率谱信号的相位编码公式中添加修正项ε，根据取整运算的性质可得ε∈(0,1)。修正项的选取属于只含上下限约束的单目标优化问题，可以通过遗传算法确定使信号的峰值因子最优时ε的取值。故ε取0.5时，信号的峰值因子降为1.74。加修正的相位编码公式为

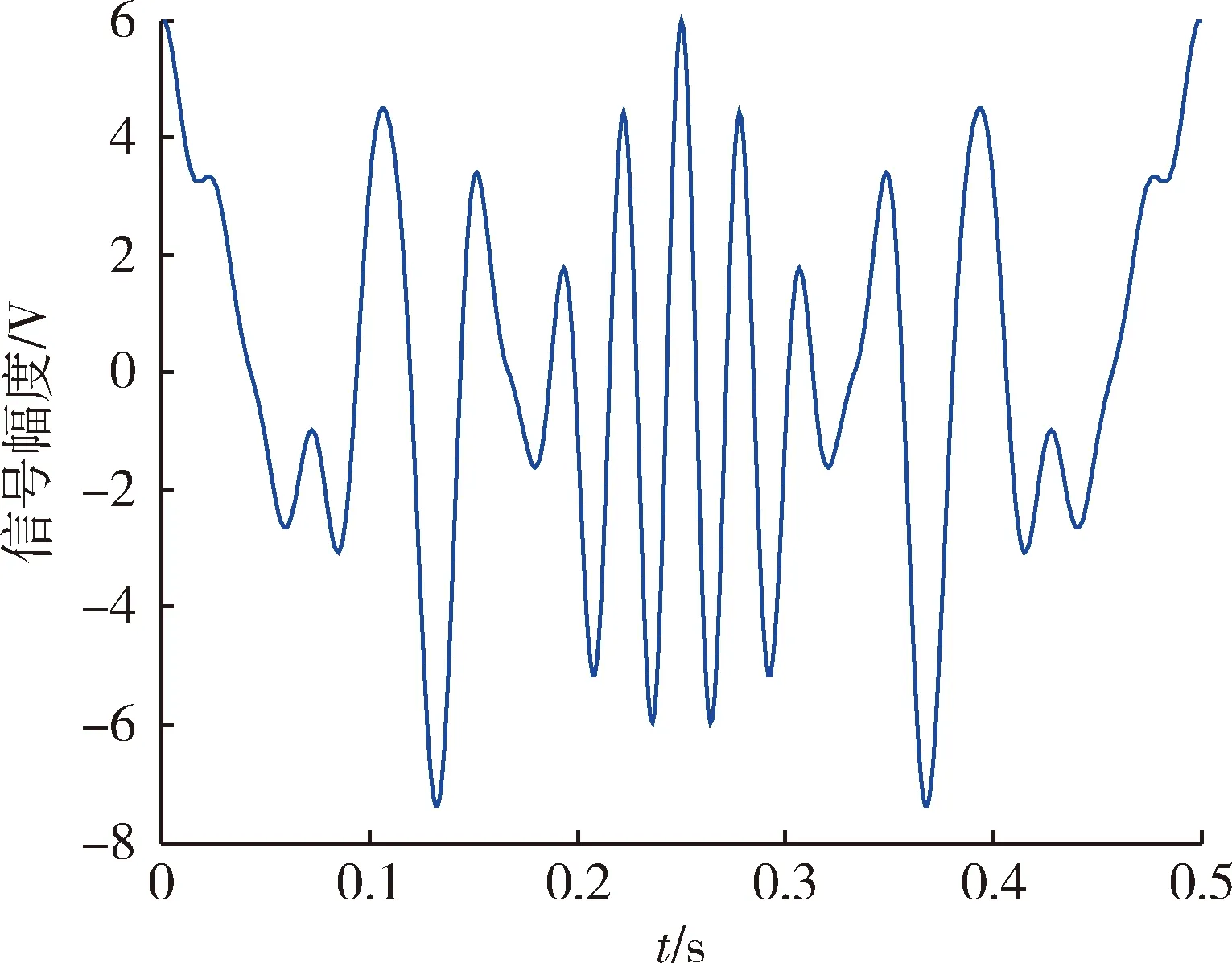
图1 多谐差相信号波形Fig.1 Waveform of SPHS

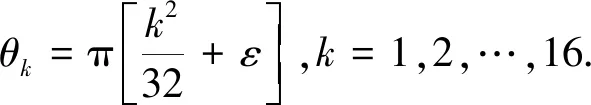
(8)

由图1可得，多谐差相信号以基波周期T为周期，作快速傅里叶变换时可通过整周截断避免谱泄漏[8]。而且信号的频谱是离散的，只在基频的整数倍上有能量，可以抑制大部分的噪声干扰[9]。通过改变基波周期T和谐波数N可以调整测试频带，实现对任意频率点模态的激活[10]。此外，该信号可以一次性激励多个频率点的模态，提高了测试速度。

2 多谐差相信号测试法改进

(9)

式中：ak，θk分别为激励信号第k次谐波的幅值和初相；bk，φk分别为系统响应第k次谐波的幅值和相移。将式(9)按照余弦函数和角公式展开得

(10)

Yn×1=An×2NC2N×1，

(11)

式中：

YT=[y(0),y(ts),y(2ts),…,y((n-1)ts)]1×n；

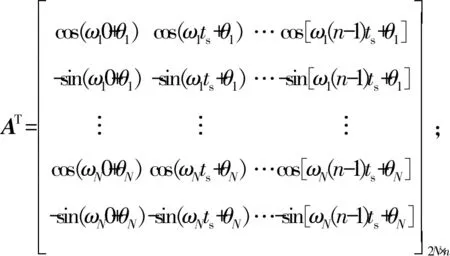
矩阵A由多谐差相信号各次谐波的角频率和初相构造，Y通过对系统的输出y(t)采样得到。当采样点数n足够大,方程个数超过未知数个数，式(11)变为超定方程组。通过求解超定方程组的C阵，即可得到系统响应中各次谐波的幅值bk和相移φk，进而得到系统的频率特性。

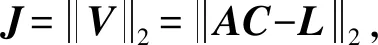
设存在正交矩阵Hn×n，使得

(12)

记Hn×nL中前2N个元素为m，其余元素记为g，对残差方程进行正交变换

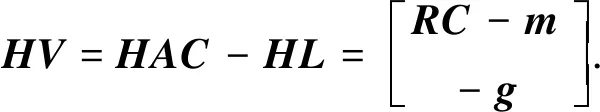
(13)

在正交变换下，向量的长度不变，对式(13)取二次范数得

(14)

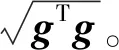
由此可得，角频率ωk对应的幅值比L(ωk)和相位差φ(ωk)为

针对奖学金、优团优干以及优秀毕业生等评优工作，也可以利用大数据对学生进行多个维度的考核。综合学生自身的上课出勤、发言以及作业质量、社团活动、课外竞赛等多个方面，利用具体提供的数据对学生展开评比，更加全面地掌握学生的学习态度、实践能力、探索精神、人际关系以及意志等多个方面。多维度的评估工作不仅仅局限于对学生的智力进行考核，还需要对学生的内在元素进行挖掘，这样也能为学生提供相应的引导，进而优化学习的模式，使学生能够更好地适应社会的发展需要，促进高校人才培养质量的提升。

(15)

(16)

上述过程可用图2表示。

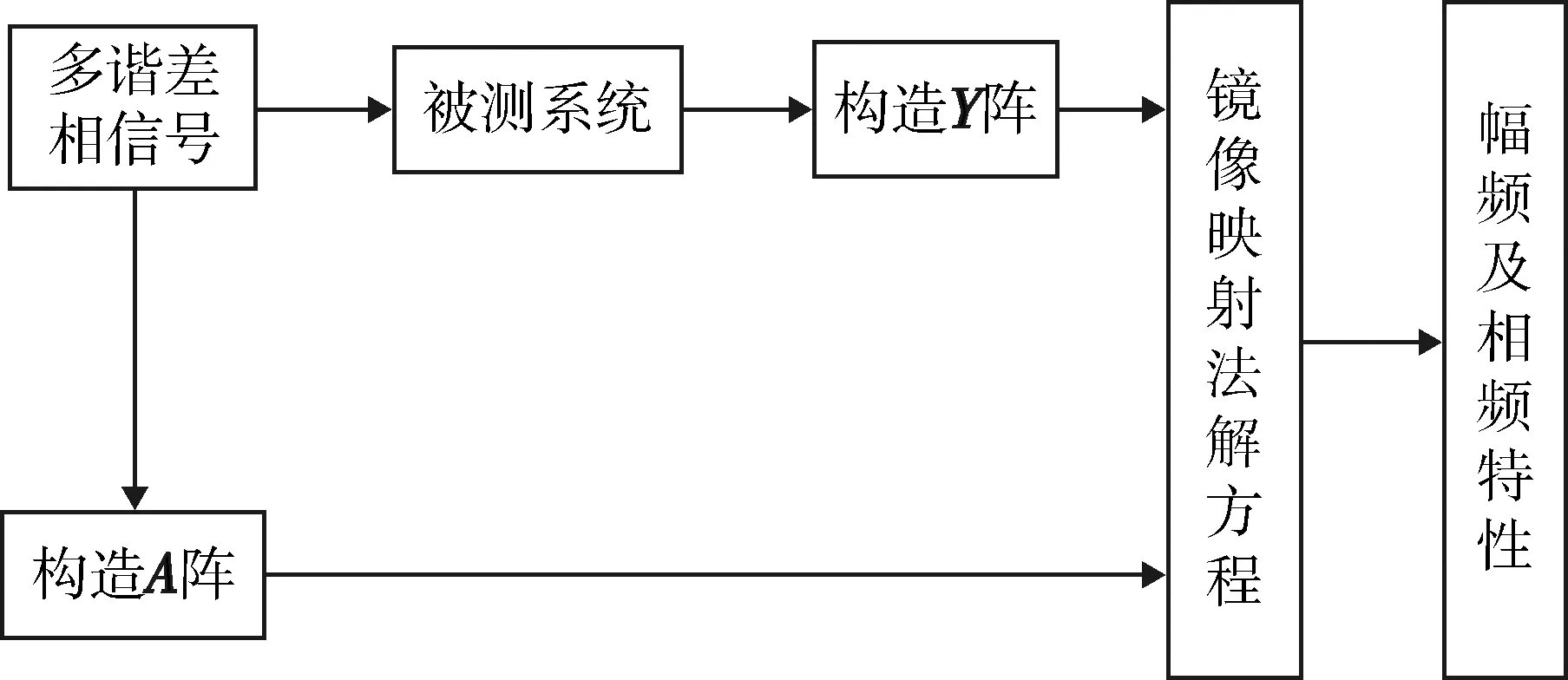
图2 多谐差相信号测试法原理Fig.2 Schematic diagram of SPHS test method

3 仿真实验与分析

为验证改进的多谐差相信号测试法的测试效果，以某型导弹的电液伺服机构为测试对象，分别使用传统的正弦相关分析法和改进的多谐差相信号测试法进行仿真。忽略系统中电液伺服阀的动态特性、结构变形和非线性摩擦等因素的影响[12]，本文研究的伺服机构由于高阶项系数较小，且频率测试范围较小，可近似为二阶的线性定常系统，其传递函数为

(17)

3.1 测试效果分析

考虑到伺服机构的最大工作频率为20 Hz，故将正弦相关分析法的测试频率选取0.1,0.5,1,5,10,15,20 Hz，多谐差相信号测试法测试频率范围0.1～20 Hz。测试信号的幅值一般取系统额定工作信号的5%～25%，且幅值尽可能大些，在同等噪声条件下可以提高信噪比[13]。故正弦相关分析法各频率点处的正弦激励信号的幅值取1 V，多谐差相信号的参数设置为：N=200，T=10 s，P=1 W，此时信号的幅值约为2 V，满足上述要求。对于参数为N=200，T=10 s，P=1 W的多谐差相信号，均匀功率谱信号、加修正的均匀功率谱信号和非均匀功率谱信号的峰值因子分别为2.26,2.03,2.17，故选择加修正的均匀功率谱信号作为激励信号，此时修正项ε=0.3，信号波形如图3所示。

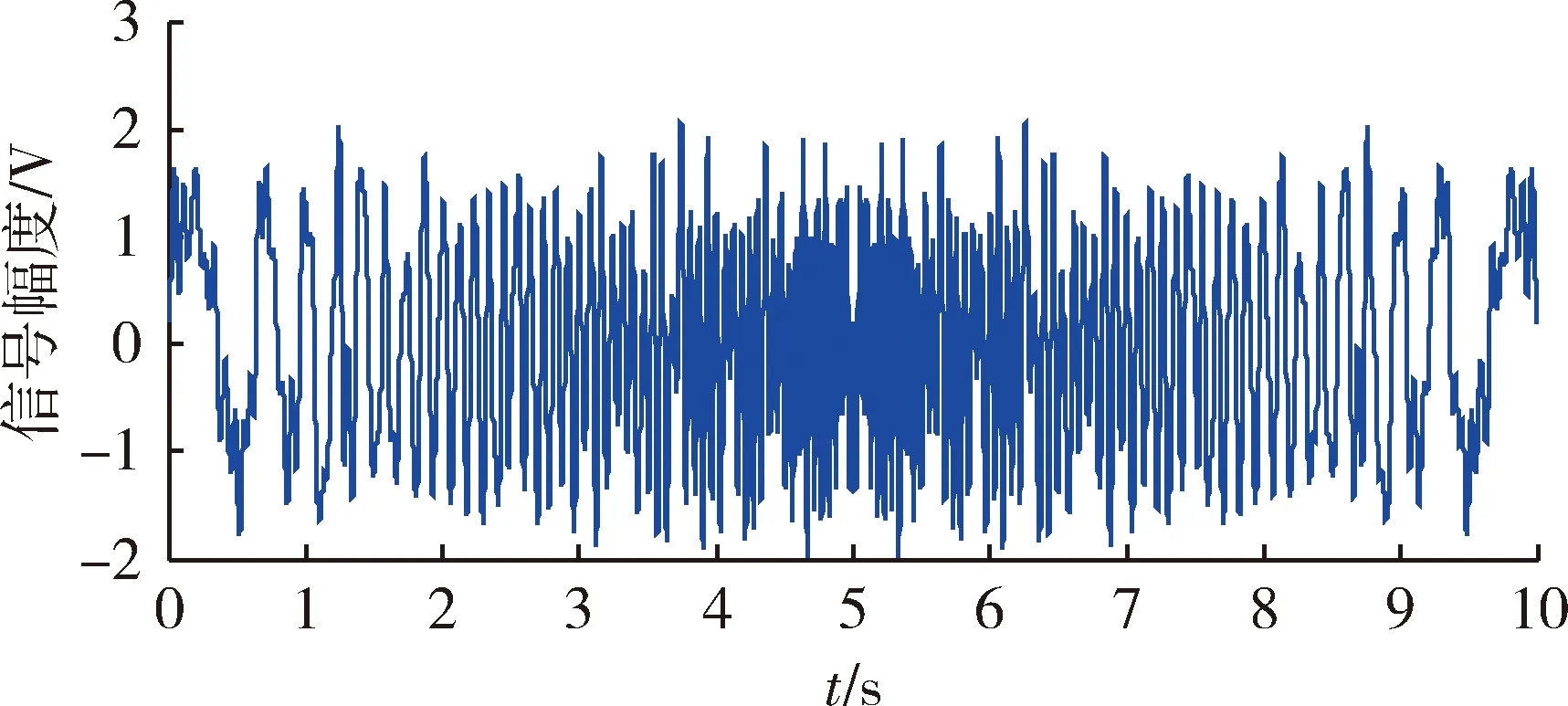
图3 激励信号波形Fig.3 Waveform of excitation signal

工程中，信号的采样频率一般选取最高频率分量的20～50倍。当选择的采样频率较低时，难以保证测试精度。当采样频率过高时，又增加了计算量，降低测试速度。由于仿真过程中信号的最高频率为20 Hz，故采样频率选择1 kHz。以伺服机构的传递函数得到的理论频率特性为基准，研究方法的测试效果。

对于正弦相关分析法，仿真过程中各频率点的扫频时间取测试频率点的最大周期。由于测试中正弦激励信号的最小频率为0.1 Hz，故每个频率点正弦信号的扫频周期为10 s。应用正弦相关分析法测得的频率特性曲线及其误差曲线如图4所示。

对于多谐差相信号测试法，频率特性的测试精度受激励时间的影响。激励时间越长，其频率特性的测试误差越小。当施加4个周期的多谐差相信号时，此时再增加激励时间对提高测试精度的作用不再明显，故选择施加4个周期的激励信号进行仿真。应用多谐差相信号测试法测得的频率特性曲线及其误差曲线如图5所示。

由图4和图5可得，在测试精度方面，正弦相关分析法的幅频特性测试误差约为0.03 dB，相频特性测试误差约为1.5°，多谐差相信号测试法的幅频特性测试误差约为0.79 dB，相频特性测试误差约为0.6°。可见，正弦相关分析法的幅频特性测试精度更高，多谐差相信号测试法的相频特性测试精度更高。在测试时间方面，正弦相关分析法需要对7个频率点处的频率特性进行测试，每个频率点正弦信号的扫频周期为10 s，故施加激励信号时间共计70 s。而多谐差相信号测试法则一次性测试200个频率点处的频率特性，施加4个周期的多谐差相信号共计40 s，时间缩短了43%，有效提高了测试速度和测试效率。

图4 正弦相关分析法测得频率特性及误差曲线Fig.4 Frequency characteristic and error curve obtained by sinusoidal correlation analysis method

3.2 抗干扰能力分析

实际测试会受到噪声干扰，为研究多谐差相信号测试法受噪声干扰的影响，在模型输出端加入均值为0、方差为0.01的高斯白噪声进行仿真[14]。

加噪声后正弦相关分析法测得的频率特性及其误差曲线如图6所示。由图6可得，正弦相关分析法由于相关运算对噪声的抑制作用较强，测试误差较小，其幅频特性测试误差约0.1 dB，相频特性测试误差约2°。

加噪声后多谐差相信号测试法仿真的响应信号如图7所示，可见伺服机构的响应信号信噪比较低。

图5 多谐差相信号测试法测得频率特性及误差曲线Fig.5 Frequency characteristic and error curve obtained by SPHS test method

多谐差相信号测试法测得的频率特性曲线及其误差曲线如图8所示。由图8可得，多谐差相信号测试法抗噪声干扰能力弱，在噪声干扰下的测试误差较大，随着频率的增加，系统响应幅值减小，噪声占很大比重，测试误差在较大范围内波动。

3.3 滤波效果分析

多谐差相信号测试法受噪声影响较大，需对采集信号进行滤波处理。为保证滤除噪声干扰的同时低频响应不被衰减，选择巴特沃斯低通滤波器[15]。设置通带截止频率为20 Hz，通带衰减为1 dB，阻带截止频率为100 Hz，阻带衰减为50 dB，可得巴特沃斯低通滤波器的阶数为4，归一化截止频率为0.05。

在同等噪声条件下使用多谐差相信号测试法进行仿真，应用巴特沃斯低通滤波器对采集信号进行滤波，得到滤波后的响应信号如图9所示。与图7相比，响应信号中的噪声已经基本滤除。

滤波前后测得频率特性及其误差曲线如图10所示。由图10可得，滤波前最大幅频特性测试误差约10dB，最大相频特性测试误差约45°，滤波后最大幅频特性测试误差约1.2 dB，最大相频特性测试误差约3°。采用巴特沃斯低通滤波器能有效滤除测试过程中的噪声干扰，显著提高频率特性的测试精度，测试误差与正弦相关分析法的测试误差相差不大，能够替代正弦相关分析法进行快速准确的频率特性测试。

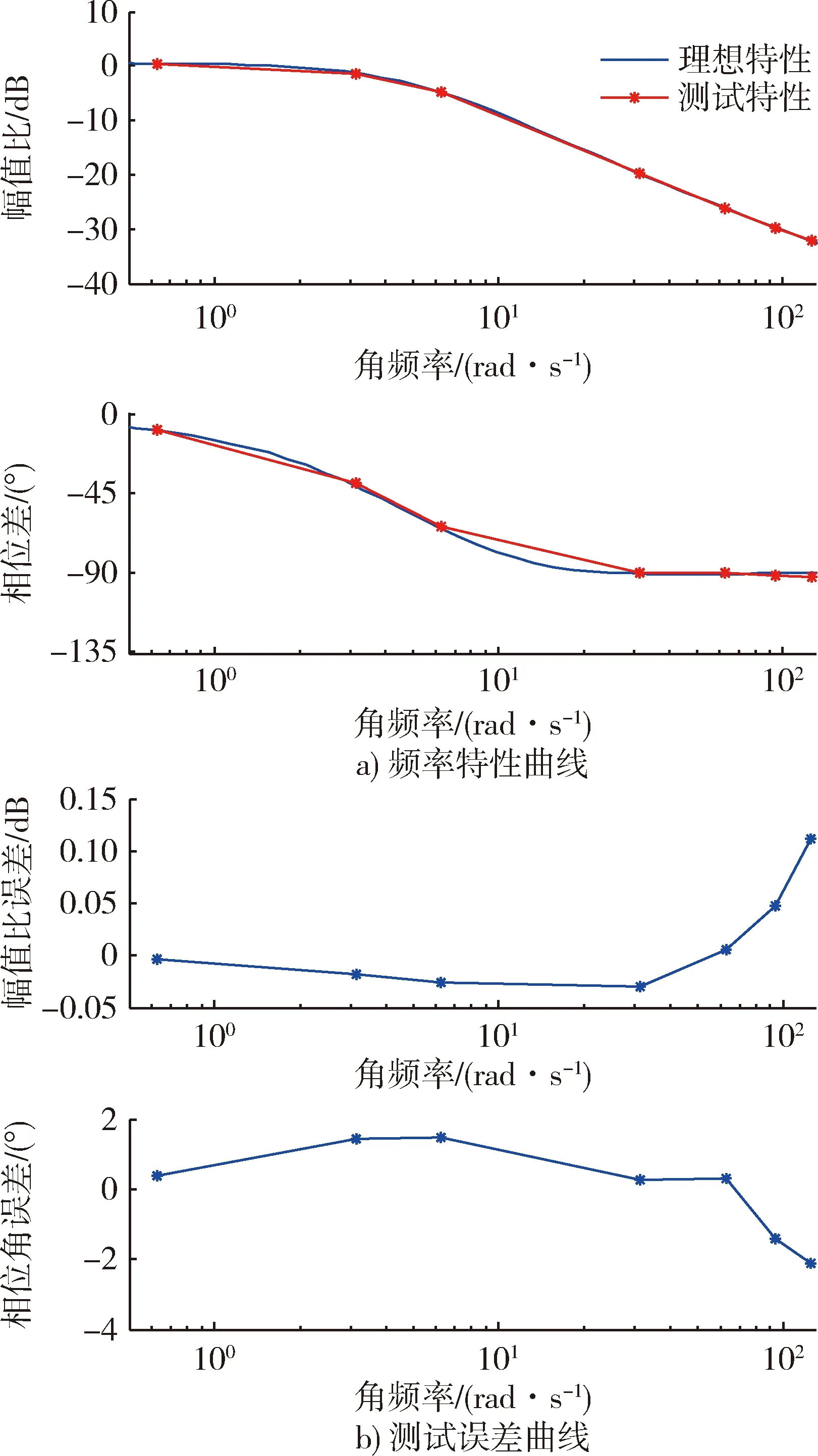
图6 正弦相关分析法测得频率特性及误差曲线Fig.6 Frequency characteristic and error curve obtained by sinusoidal correlation analysis method

图8 多谐差相信号测试法测得频率特性及误差曲线Fig.8 Frequency characteristic and error curve obtained by SPHS test method

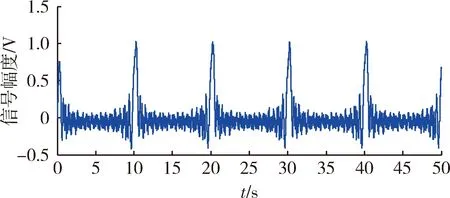
图9 滤波后的响应信号波形Fig.9 Waveform of filtered response signal

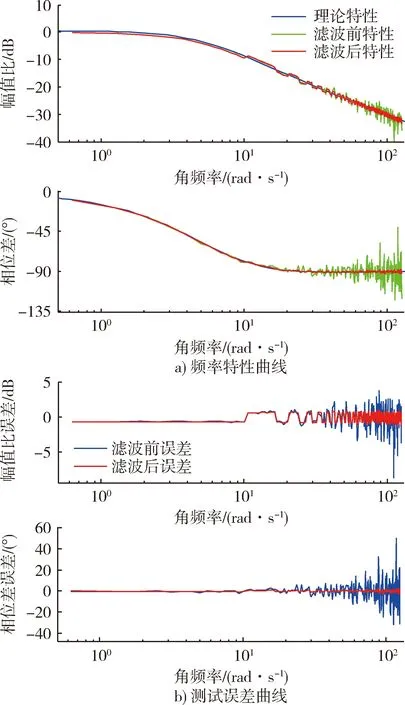
图10 滤波前后测得的频率特性及误差曲线Fig.10 Frequency characteristic and error curve before and after filtering

4 结论

本文对多谐差相信号测试法进行了改进，并以某型导弹的伺服机构为测试对象，分别在无噪声和有噪声的条件下使用传统的正弦相关分析法和改进的多谐差相信号测试法进行仿真。主要结论如下：

(1) 无噪声条件下，正弦相关分析法的幅频特性测试精度更高，多谐差相信号测试法的相频特性测试精度更高。相比之下，多谐差相信号测试法的测试速度更快，测试效率更高。

(2) 同等噪声条件下，正弦相关分析法的抗干扰能力更强，多谐差相信号测试法需要对采集信号进行滤波处理。

(3) 对多谐差相信号测试法采用巴特沃斯低通滤波能够有效滤除测试中的噪声干扰，显著提高了测试精度，可以替代正弦相关分析法进行快速准确地频率特性测试。