反辐射无人机抗同步闪烁诱饵诱偏方法

张逸楠，彭世蕤，冷毅，任明秋

(空军预警学院，湖北 武汉 430019)

0 引言

反辐射无人机是一种利用敌方雷达辐射的电磁信号发现、跟踪以至最后压制或摧毁雷达的武器系统[1-3]。当今无论是反辐射无人机或反辐射导弹装备的导引头上都广泛采用单脉冲测角跟踪技术，在导引头设计中，为消除信号的多径效应对导引头产生的影响，多采用脉冲前沿跟踪技术[4]。为了保护雷达自身，雷达信号前沿会被诱饵辐射的信号前沿掩护，从不同诱饵子站的信号前沿超前雷达信号的方式看，有诱饵前沿固定超前、诱饵慢速闪烁、诱饵快速闪烁、相干诱饵等[5]。导引头采用前沿测向可进行正确测向，但测向结果将随诱饵前沿变化而变化，导致命中概率降低[6]。仅仅通过前沿跟踪，只能引导反辐射武器靠近雷达阵地，识别并剔除其中前沿超前的那个诱饵，无法从中识别出雷达[5]。因此，反辐射无人机攻击配诱饵雷达系统的一种战术思想可确立为先摧毁诱饵，再攻击雷达。对于抗闪烁诱偏而言，本文先通过量测转换将实时变化的角度测量信息转换成相对固定的目标位置信息，将该目标位置信息形成一个知识样本空间，然后利用基于灰色理论的数据处理方法进行异常值剔除、灰色距离测度与灰色关联熵计算，得出同步闪烁诱饵的闪烁周期，最后调整无人机的末制导测角机动调整周期等于该同步闪烁周期，使无人机始终跟踪某一个诱饵，而忽略其他诱饵，达到有效毁伤至少一个诱饵的目的。

1 目标位置量测转换

闪烁诱偏在时序上划分为同步闪烁诱偏和异步闪烁诱偏[7]，异步闪烁诱偏的诱饵独立地发射诱偏信号，没有时序上的严格限制；同步闪烁诱偏的诱饵按时序周期性地发射诱偏信号，在任一时刻只有一个诱饵发射诱偏信号，如图1所示，其中，诱饵的“闪烁模式”和“闪烁周期”是分析反辐射导引头截获多点源辐射信号的重要因素。

图1 雷达诱饵同步闪烁时序示意图Fig.1 Schematic diagram of the timing sequence between radar and decoys

“闪烁模式”主要是指多点源信号在辐射持续时间、相对先后次序上的各种组合情况；“闪烁周期”则主要是指完成1次“闪烁模式”所需的时间。由于配诱饵的雷达系统(雷达和诱饵)多为固定目标[8]，可以通过量测转换将随反辐射无人机姿态和位置变化的指向角度信息转换成相对固定的目标位置信息。

1.1 无人机末制导攻击建模

无人机末制导攻击模型主要参考文献[9]中反辐射导弹运动模型的位置简化递推算法。当无人机未进入俯冲攻击阶段时，作平飞运动，无俯仰面的姿态调整，仅调整方位面；当导引头框架角大于某一固定值时，无人机进入俯冲攻击阶段，分别根据俯仰面与方位面的测角情况进行俯仰面与方位面的姿态调整，再进行运动的合成，最终形成无人机的攻击轨迹。

1.2 目标地面位置估计

建立大地坐标系Oxyz、机体坐标系Oxmymzm、天线坐标系Oxpypzp与平动坐标系Oxdydzd,如图2所示，坐标系间转换关系可参考文献[9]。

图2 4个坐标系定义Fig.2 Definition of four coordinates

设目标雷达及其诱饵位于Oxz平面上，反辐射无人机处于空间某点。无人机测得的辐射源角度信息用天线坐标系下单位矢量的指向表征，经过一系列坐标转换可得到其在平动坐标系下的矢量，求解这个矢量与地面的交点，可得到目标在大地坐标系下的位置信息。

设反辐射无人机在天线坐标系下的测角信息为(α,β)，α为方位角测角值，β为俯仰角测角值，描述了目标偏离波束指向中心的角度。建立目标在天线坐标系下的目标指向单位矢量e=(cosβcosα,sinβ,cosβsinα)，经过由天线坐标系转换到机体坐标系，再转换到平动坐标系，可以得到这个矢量在平动坐标系下的坐标e=(xd,yd,zd)。通过机载的导航定位系统，可以实时得到无人机的航向、姿态、速度及位置等参数，设此时的无人机在大地坐标系下的位置为c=(xc,yc,zc)，如图3所示，A点为平动坐标系原点在大地坐标系Oxz平面的投影点，B点为目标单位矢量与Oxz平面的交点，即目标位置点，可知A点在平动坐标系中的坐标为a(0,-yc,0)，大地坐标系Oxz平面在平动坐标系中的坐标为y=-yc，建立以下方程组：

(1)

解出目标位置B点在平动坐标系中的坐标后，再经过平动坐标系与大地坐标系的坐标转换矩阵，可得出大地坐标系下的目标位置。

图3 实时解算目标位置示意图Fig.3 Schematic diagram of calculating the target position in real time

2 基于灰色理论的闪烁周期估计

灰色系统理论主要用于求解无经验、数据较少的不确定性问题。而反辐射无人机攻击配诱饵雷达过程中获得的数据样本量较小、分布规律随机变化，因而数据样本集是一个典型的灰色系统。

设无人机经过量测转换得到目标二维位置点集P={x1,x2,…,xn}，灰色理论要求数据样本中的数据数目不得低于3个[8]，将目标位置点集P中的元素按照3个位置信息作为一组形成一个数据样本集，按照时序，用测得新位置代替旧位置，形成一系列的样本集P1={x1,x2,x3},P2={x2,x3,x4},…。

首先，确定作为参考的被估计参数x0，即某一诱饵的估计位置。由同步闪烁诱饵的工作模式易知，无人机经过实时量测转换得到的目标位置点集将体现3个诱饵位置的周期性变化，可利用前几个测得的样本集二维数组各行的均值的周期性确定被估计值x0，该均值出现突变时，即为目标位置点集中某一诱饵位置与另一诱饵位置之间的转换点。因此，选取均值突变点前一个值作为被估计值x0，即随机选取了某一个诱饵的估计位置值。

然后，将样本集Pi={xi,xi+1,xi+2}与被估计参数x0进行灰色关联。数据样本xi与被估计参数x0的灰色距离测度通过式(2)[8]计算得到：

(2)

被估计参数x0与样本集Pi={xi,xi+1,xi+2}的灰色关联熵Shi的计算方法如下：

(3)

从灰色关联熵的定义可以看到，灰色关联熵是被估计值x0与样本集Pi灰色距离测度的加权求和。因此灰色关联熵可以看作估计值与样本集之间的灰色关联度的度量，也可以看作估计值与样本集在拓扑和距离上的关联紧密程度的度量[11]。

因导引头存在测角误差，测角误差导致诱饵位置信息转换的误差，因此导引头多次测得的同一个诱饵的位置信息将在诱饵真实位置信息的一定范围内波动。由于位置误差的存在，先对各样本集内位置信息进行异常值剔除，异常值剔除步骤参考文献[8]。

剔除完各样本集内异常值后，实时计算每一组样本集与被估计值x0的灰色关联熵，计算流程如图4所示。首先设定一个均值突变门限Δ，确定被估计值x0；然后设定灰色关联熵门限η，实时计算每一个样本集被估计值x0的灰色关联熵Sh，其应呈现出周期性，选取非临近的、过门限的2个灰色关联熵之间的间隔时间作为闪烁周期的估计值；若有2个及以上不为0的闪烁周期估计值且其差值在一个诱饵持续发射诱偏信号的时间内，则以此为最终闪烁周期值；若算出的最终闪烁周期值比无人机机动调整周期小，则取最终闪烁周期刚好大于无人机机动调整周期的最小整数倍的数值，以此为依据改变无人机机动调整周期，即无人机2次调整飞行姿态之间的间隔时间。这样使反辐射无人机稳定跟踪被估计值x0所对应位置的诱饵，而不跟踪其他诱饵信号，最终达到对该诱饵的毁伤目的。

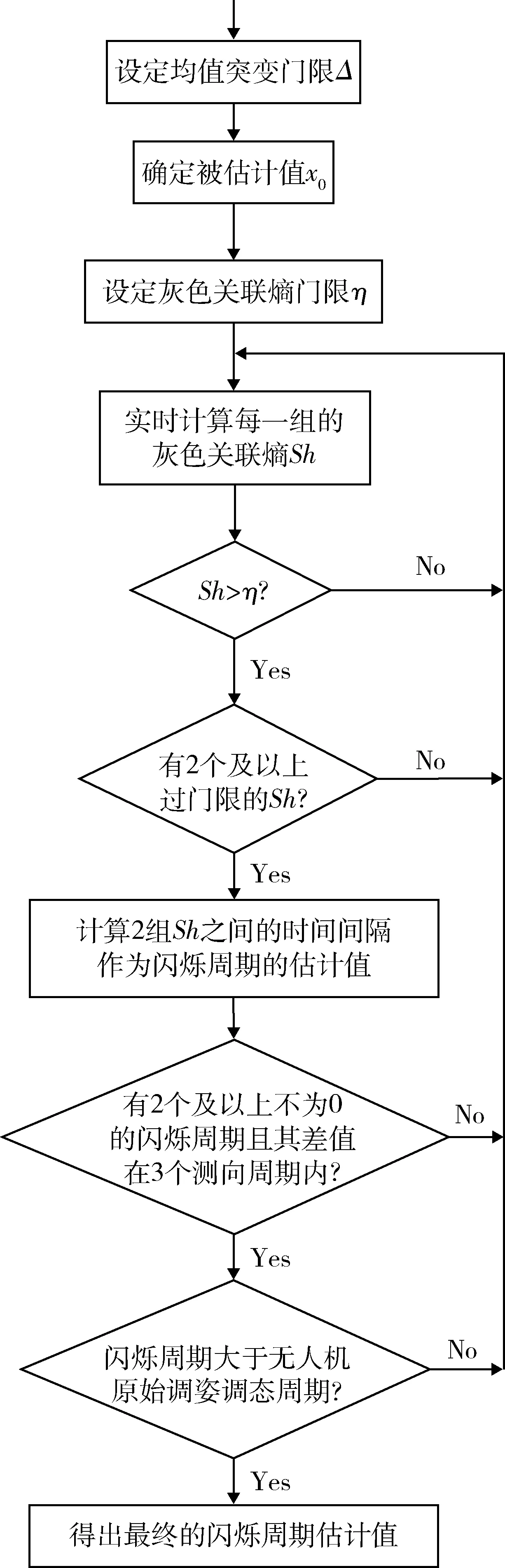
图4 闪烁周期计算流程Fig.4 Calculation process of the blinking period

3 仿真校验

3.1 算法校验

设无人机攻击目标为一雷达配备3闪烁诱饵系统，雷达与诱饵间距离为300 m的菱形布阵，以使雷达及诱饵获得较高的生存概率[12]。雷达初始坐标(-260，0，0) m，诱饵1(0，0，150) m，诱饵2(260，0，0) m，诱饵3(0，0，-150) m，η=0.8[9]，如图5所示。仿真条件为：反辐射无人机初始飞行高度2 000 m，初始坐标(-4 924，2 000，868) m，设入侵角为无人机攻击时飞行方向在大地坐标中投影与Ox轴的夹角，本次仿真取-10°；取由噪声引起的测角误差为0.036°[13]，Δ=1.26；诱饵辐射场初始相位对雷达诱饵生存概率影响相对较小，设雷达与3诱饵发射信号的初相皆为0，发射信号频率为3 GHz；诱饵闪烁模式为：按照诱饵1、诱饵2与诱饵3的顺序依次发射信号，闪烁周期取0.75 s；无人机水平与俯仰平面分别采用双基线干涉仪比相法测向体制，半波束宽度为60°，天线间间隔为0.05 m，巡航速度为50 m/s，初始天线指向角为-10°，即导引头天线法向与无人机机身的夹角，向下为负；俯冲攻击角度为-75°，横向过载2，俯冲向下过载4，测向传输周期为0.03 s，初始无人机机动调整周期为0.03 s。无人机直接打击同步闪烁诱饵的仿真如图5～7所示；无人机采取文中算法打击同步闪烁诱饵进行的仿真如图8～10所示。

给出的2组仿真实验对比了应用算法前后的无人机方位面、俯仰面测角变化情况与无人机攻击航迹；算法在无人机俯冲攻击后运行，主要关注无人机俯冲攻击前后的测角情况。图5,8给出无人机攻击航迹；图6,7,9,10给出无人机测角变化情况。本次仿真中无人机俯冲攻击时刻约为无人机起飞后的第89 s，则截取无人机飞行第60 s到最终落地爆炸的测角变化进行说明。

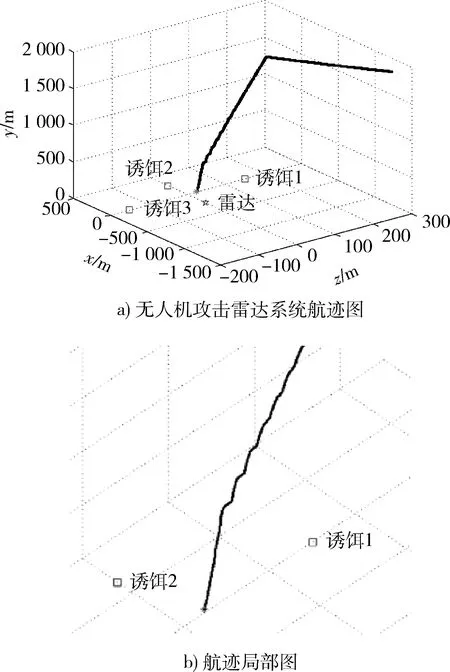
图5 未加算法的无人机末制导攻击情况Fig.5 Situation of UAV′s terminal guidance without algorithm

图6 未加算法的无人机方位角变化情况Fig.6 Changing of UAV′s azimuth without algorithm

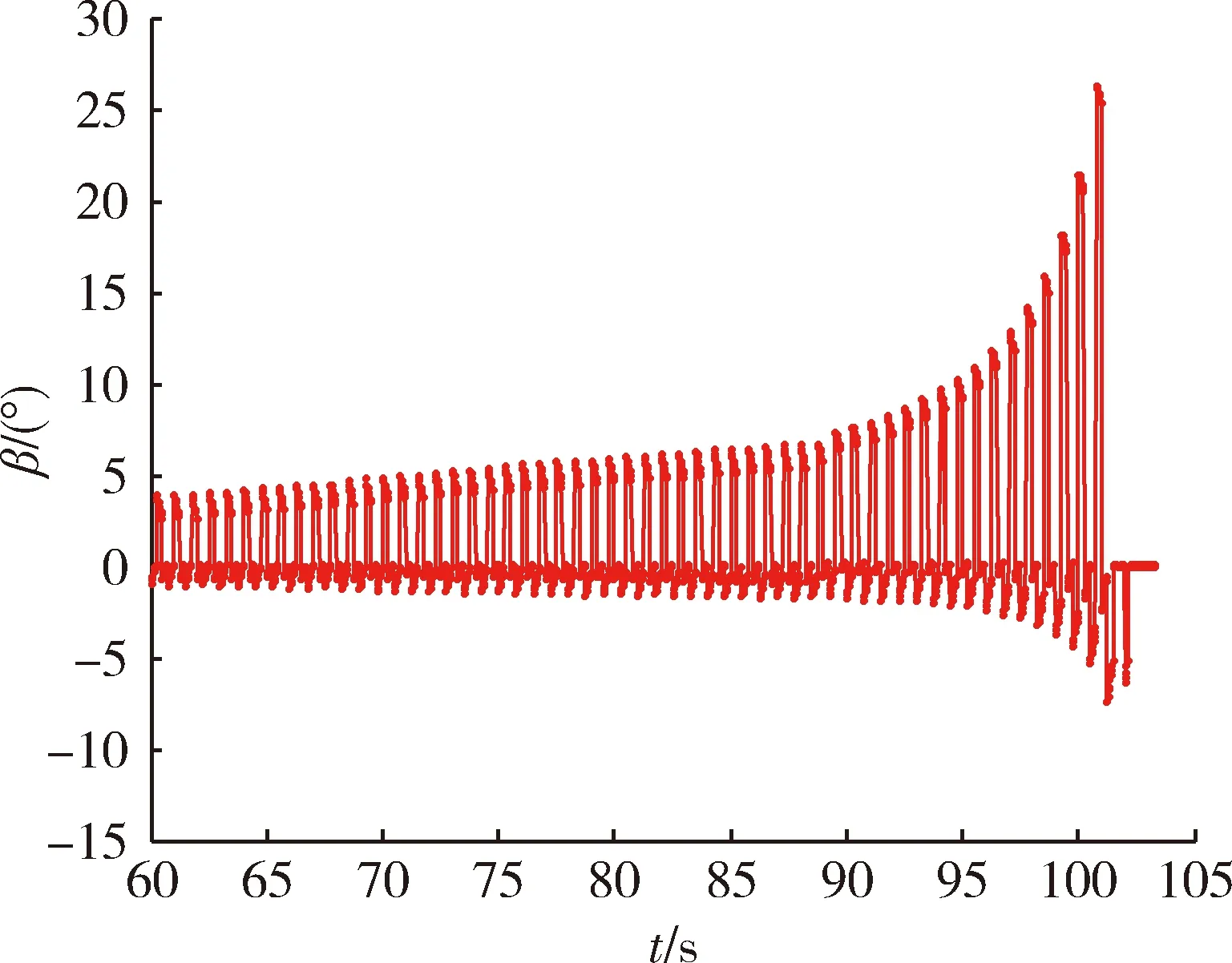
图7 未加算法的无人机俯仰角变化情况Fig.7 Changing of UAV′s pitch angle without algorithm

图8 加算法后的无人机末制导攻击情况Fig.8 Situation of UAV′s terminal guidance with algorithm

由图5可见，攻击路径粗糙，即使最后有诱饵脱离了无人机的视场范围，无人机也因无法及时机动，最终无法造成有效毁伤。由图6,7可见：反辐射无人机测角变化从数据跳变大小和方向可以大致判断出有3部诱饵且交替变化。这说明，在末制导攻击阶段，导引头天线在方位面和俯仰面测角数据随着诱饵交替靠前的变化而呈周期跳变样式；在3诱饵交替靠前时刻，导引头测得的跳变角度数据大小也不一样；从数据的不断跳变到归零的变化趋势可以看出，无人机飞控系统将按照导引头末制导测角采样周期上传的测向数据适时调整攻击姿态，使无人机始终朝着误差角减小的方向调整，由于导引头天线数据在3诱饵间不断跳变，从而控制机体反复跟踪3诱饵。

图9 加算法后的无人机方位角变化情况Fig.9 Changing of UAV′s azimuth with algorithm

图10 加算法后的无人机俯仰角变化情况Fig.10 Changing of UAV′s pitch angle with algorithm

由图8可见，无人机在俯冲攻击后，很快锁定跟踪某一诱饵(在本次仿真中为诱饵3)，攻击路径平滑，最终无人机落地爆炸点离诱饵3距离为1.725 3 m，对诱饵3进行了有效毁伤。由图9,10可见：采取本文的算法后，无人机测角采样周期未改变，但在第92 s时，即从俯冲攻击开始约3 s时，算法估算出同步闪烁诱饵闪烁周期，然后依据该闪烁周期调整无人机的机动调整周期，无人机的机动调整周期变长，并且每次依据的角度值都为同一诱饵的测角值，无人机不再产生追摆；随着无人机的机动调整，测角值在不断减小或几乎为0，说明无人机已锁定该诱饵进行跟踪。

3.2 闪烁周期对算法精度的影响

以闪烁周期0.3 s为例，取反辐射无人机的有效毁伤圆概率误差为20 m，用蒙特卡罗的方法重复1 000次攻击过程仿真，统计无人机落地点的频数，画出无人机应用算法后攻击落点频数分布图如图11,12所示。

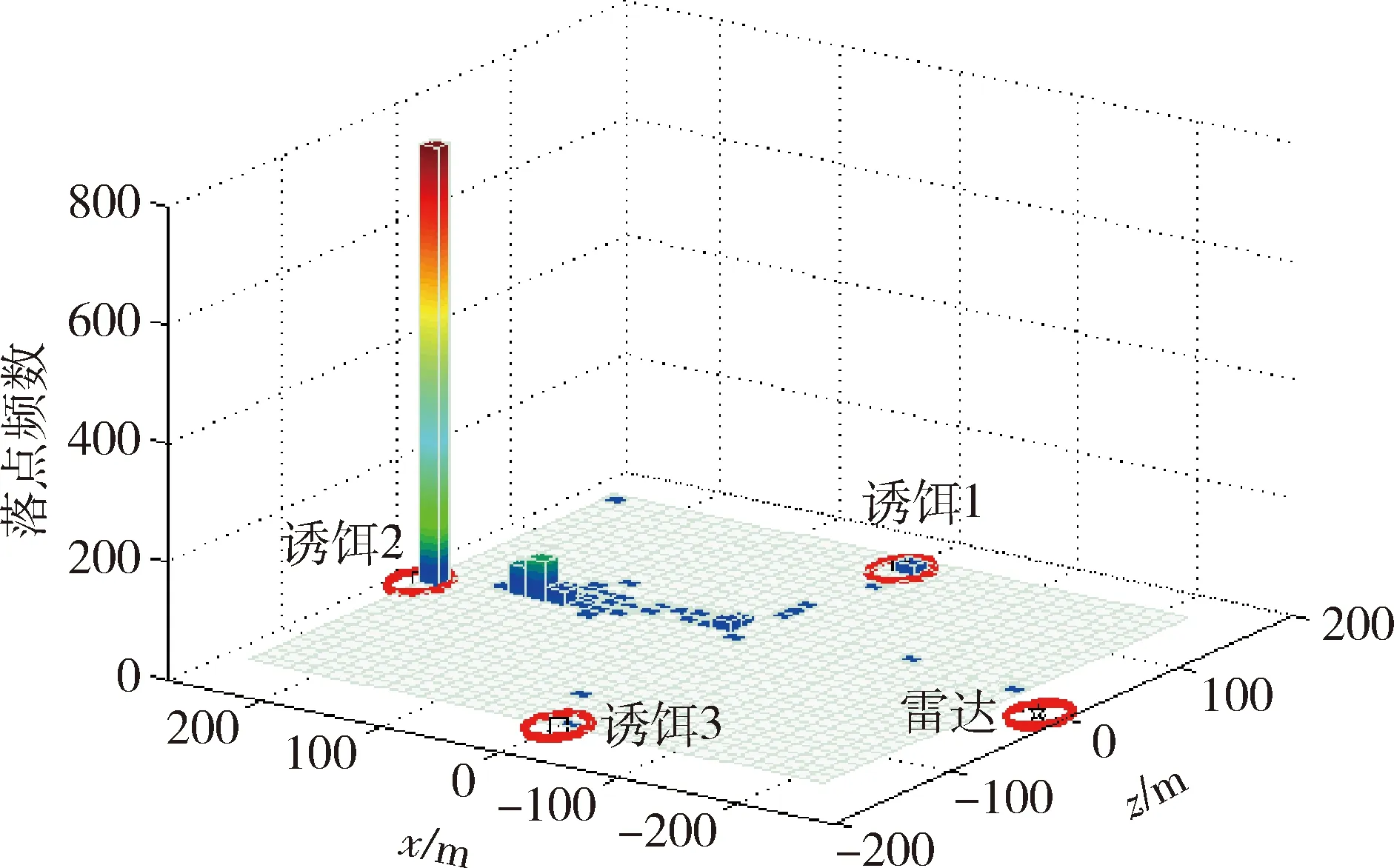
图11 无人机落点分布频数三维图Fig.11 Frequency of UAV′s hitting points

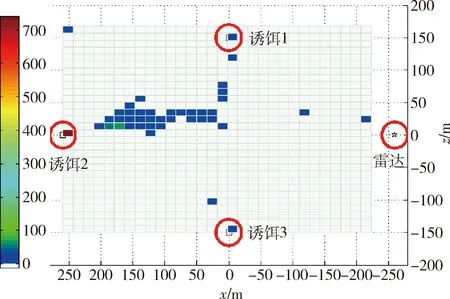
图12 无人机落点分布二维图Fig.12 Two-dimensional map of UAV′s hitting points

无人机有效毁伤诱饵1的次数为16次、有效毁伤诱饵2的次数为741次、有效毁伤诱饵3的次数为1次，有效毁伤诱饵的概率达到了75.8%，不能百分百打中诱饵的原因是存在由噪声引起的测角误差，若去掉测角误差影响，则在该情况下可100%有效毁伤诱饵。

在影响诱偏效果的参数中，闪烁周期是一个非常重要的参数，如果闪烁周期过低，导引头会平均误差，跟踪诱饵源的能量重心位置；如果过高，导引头会稳定跟踪诱饵源之一[14]。参考文献[15]中闪烁周期的设置范围，本文假设在闪烁周期大于0.015 s时，导引头天线都可检测出不同辐射源振幅变化情况，取闪烁周期分别为3，2，1.5，0.9，0.75，0.6，0.3，0.24，0.15，0.09，0.04，0.03，0.024，0.018,0.015 s,其余仿真条件与3.1一致的条件下，用蒙特卡罗的方法重复1 000次攻击过程仿真，计算无人机打中诱饵的概率。

由图13可以看出：当诱饵的同步闪烁周期不大于且能整除导引头的测角采样周期时，导引头可以稳定地跟踪某一诱饵并完成对该诱饵的有效毁伤。此结论不难理解：此时导引头的每一次测角将刚好测到同一个诱饵发出的诱偏信号，可以稳定地跟踪该诱饵；除了这种情况以外，无人机无法有效毁伤配同步闪烁诱饵的雷达系统。

图13 无人机在无算法的情况下毁伤诱饵概率描点图Fig.13 Damage probability of UAV without algorithm

由图14可以看出：在应用了算法后，无人机有效毁伤诱饵的概率随着诱饵的同步闪烁周期的变化而变化；根据仿真结果，可以将同步闪烁周期大致分为3段：第1段为闪烁周期为1 s及以上;第2段为闪烁周期为导引头测角采样周期(在仿真中为0.03 s)至1 s;第3段为导引头测角采样周期(0.03 s)及以下；当闪烁周期的值处于第1段时，无人机有效毁伤诱饵的概率普遍较低，随着闪烁周期的值增大，无人机有效毁伤诱饵的概率越来越低，当闪烁周期的值增大到一定程度，无人机无法有效毁伤诱饵，原因在于应用该算法使得无人机机动调整周期与闪烁周期一样较长，末制导攻击时无人机机动调整间隔较长，由于机动能力的限制，无人机反而机动更慢，无法有效毁伤诱饵；当闪烁周期的值处于第2段时，无人机有效毁伤诱饵的概率普遍较高，随着闪烁周期的值减小，无人机有效毁伤诱饵的概率越来越高，当闪烁周期的值减小到一定程度，即闪烁周期的值比较接近无人机测角采样周期值时，无人机能完全有效毁伤诱饵，原因在于，算法能及时算出闪烁周期值，无人机机动调整时间也较短，可以及时进行对某一诱饵的机动调整；当闪烁周期的值处于第3段，诱饵的同步闪烁周期不大于且能整除导引头的测角采样周期时，与不应用算法一样，无人机能有效毁伤诱饵，其他情况下，应用算法后无人机的毁伤概率也较高。

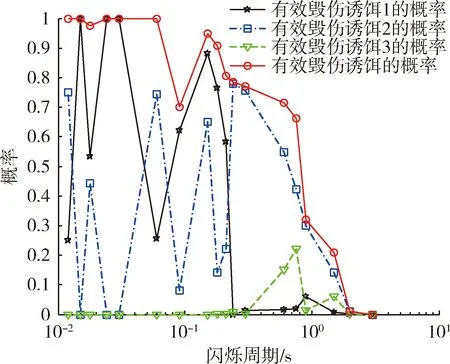
图14 无人机在有算法的情况下毁伤诱饵概率描点图Fig.14 Damage probability of UAV with algorithm

4 结束语

本文首先分析了闪烁诱饵诱偏反辐射无人机的原理及效果；提出了一种通过提取闪烁周期来对抗同步闪烁诱饵的方法；最后，进行Matlab仿真分析了该算法的有效性及诱饵的闪烁周期对该算法的影响。仿真结果表明，在一定的诱饵闪烁周期内，本文所提出的方法可以有效对抗同步闪烁诱饵，为反辐射无人机抗诱饵诱偏提供了一种新方法。