核心素养下高中数学概念课教学策略①
蔡海涛 林运来
(1.福建省莆田第二中学 351131 2.福建厦门大学附属实验中学 363123)
1 问题提出
中学数学是由概念、命题经推理组成的逻辑体系.概念、命题和推理是逻辑思维的三大基本形式.其中,概念是逻辑思维的细胞,是反映事物本质属性和特征的思维形式.数学概念是反映现实世界空间形式和数量关系本质属性的思维过程.可见,数学概念在数学学习中占有重要位置.因此,数学概念的教学理应回归概念的本源.但是,在概念教学中,教师往往采用“一个定义,几项注意”的方式,讲完概念就做题,做了题才发现学生对概念一知半解,则让他们做更多的题,凡此种种,导致课堂上给学生带去的不是享受、成功、体验,而是单调、无趣和一知半解.
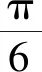
A.37.5分钟 B.40.5分钟
C.49.5分钟 D.52.5分钟
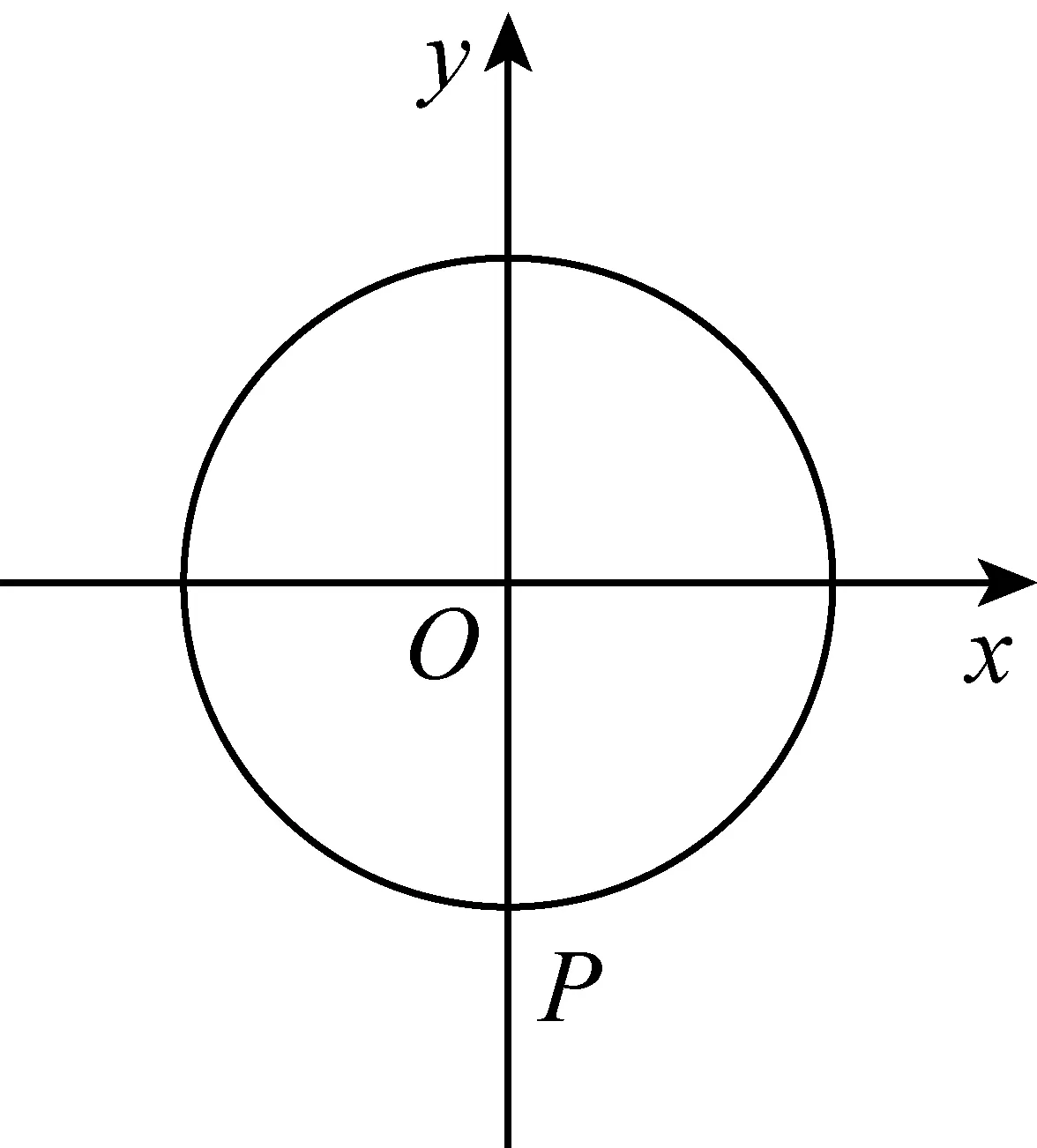
图1
本题以匀速圆周运动为背景,考查任意角三角函数的定义、三角函数的图象与性质等基础知识.根据任意角三角函数的定义、三角函数的图象与性质等知识,或结合平面几何知识进行直观判断,不难得出正确选项.可是全省实测均分仅为1.8分,让人感到出乎意料.考试结束后对部分考生进行访谈,了解其答题情况后,发现很多学生错误的原因在于不会从题目中获取有用信息,不会利用三角函数的概念来解答.
在高考复习中,是不是我们在刷题的路上走得太远了?是否应该停下来思考我们丢了什么?新时期的高考已经从能力立意到素养导向,所以概念教学需要与时俱进,改变教学方法,以培养学生的数学核心素养为目标.笔者谈谈自己的一些思考与体会,期与同行交流.
2 核心素养下的高中数学概念教学
2.1 合理制定教学目标,明确核心素养的植入点
案例1椭圆的概念
建构椭圆的概念,可制定的教学目标是:经历从具体情景中抽象出椭圆的过程,利用细绳画椭圆的方法将椭圆定义具体化,加强椭圆的定义和图形特征的理解,掌握椭圆的定义,提升直观想象素养.完成该教学目标可做如下教学设计:
通过多媒体展示生活中图形(图2)及卫星的运行轨迹(图3),让学生经历从具体情境中抽象出椭圆的过程,通过观察、探究揭示椭圆的几何特征,发展直观想象素养.

图2
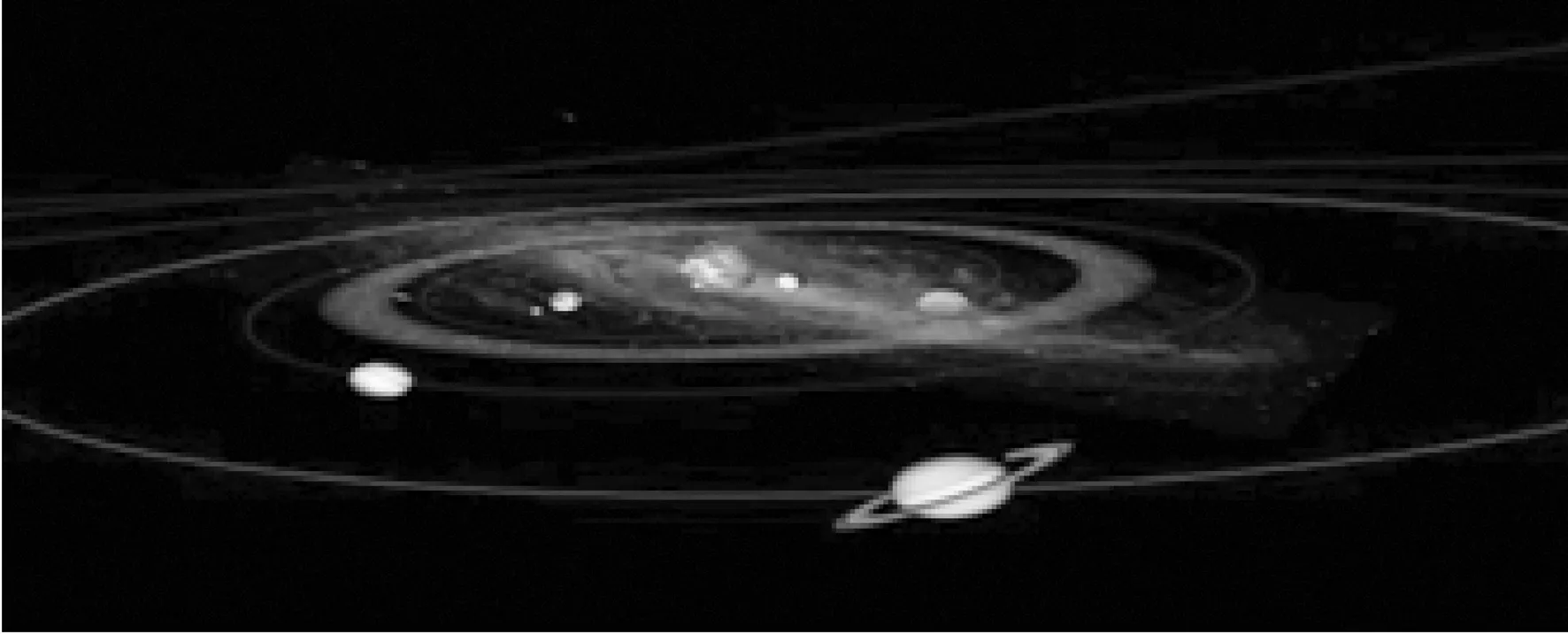
图3
接下来,引导学生拿出事先准备好的绳子,小组合作做如下的实验:
(1)取一条细绳;
(2)把它的两端固定在板上的两点F1,F2;
(3)用铅笔尖把细绳拉紧,在板上慢慢移动,观察画出的图形(图4、图5).
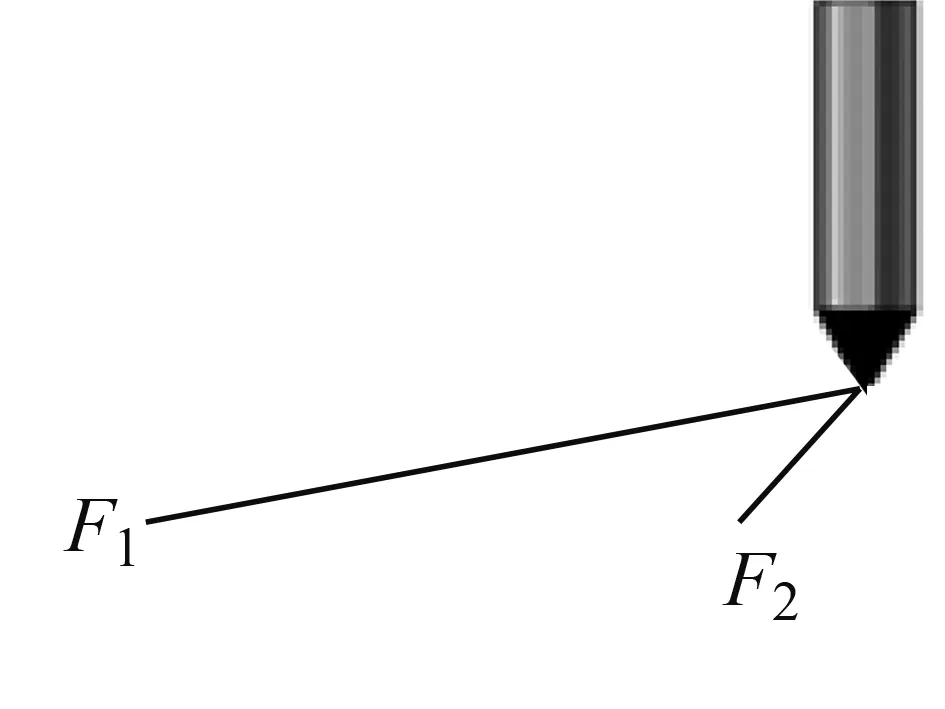
图4
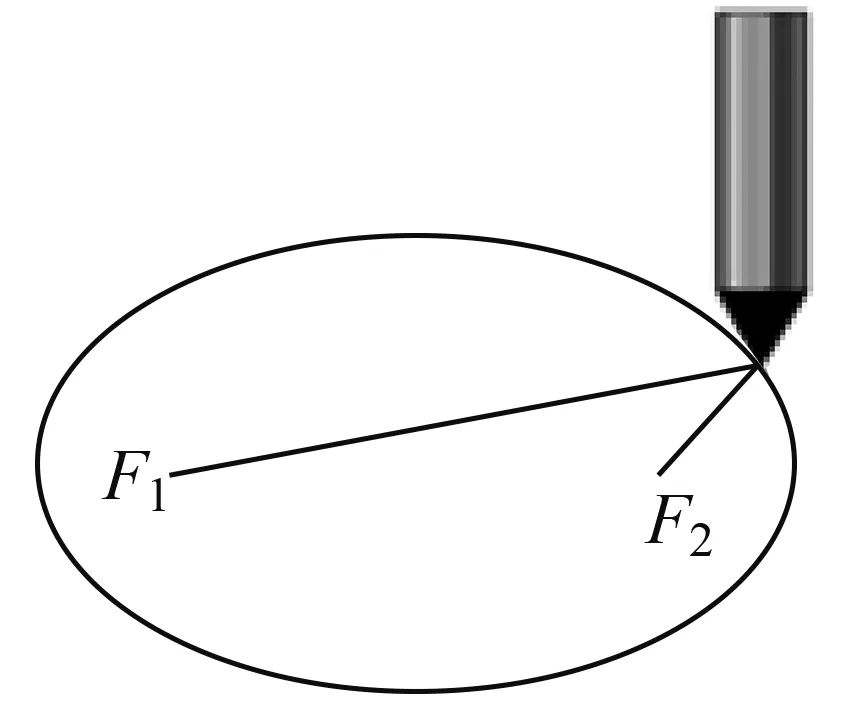
图5
学生画好后,教师利用几何画板验证椭圆的形成过程,通过实验,容易观察得到的图形为椭圆.在几何画板的展示中,引导学生思考在椭圆的形成过程中哪些量改变,哪些量不变?通过观察,学生发现到铅笔尖对应点M与F1,F2的距离|MF1|,|MF2|改变,而|MF1|+|MF2|及|F1F2|的值不变.接着,教师引导学生类比圆的定义引出椭圆的定义.此时,学生往往会回答:平面内与两个定点距离之和为定值的点的轨迹为椭圆.教师应引导学生再仔细考虑有没有不足之处,提出如下问题:
问题1改变两图钉之间的距离,使其与绳长相等,画出的图形还是椭圆吗?

图6
问题2绳长能小于两图钉之间的距离吗?

图7
由此得到结论:绳长记为2a,两定点间的距离记为2c(c>0).
(1)当2a>2c时,轨迹;
(2)当2a=2c时,轨迹;
(3)当2a<2c时,轨迹;
由以上的数学实验再类比圆的定义,引导学生对椭圆进行定义.在学生观察实验中,从提出问题、建立模型、求解模型、检验结果再完善模型,发展了数学建模的素养.
2.2 精心设计问题情境,抓准核心素养的着力点
案例2对数的概念
对数概念对高一学生有一定的难度,为了更好地让学生理解,可设置一些问题,找准核心素养的着力点.
教师创设问题情境:“一尺之棰,日取其半,万世不竭”.
问题1(1)取5次,还有多长?(2)取多少次,还有0.125尺?
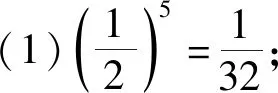
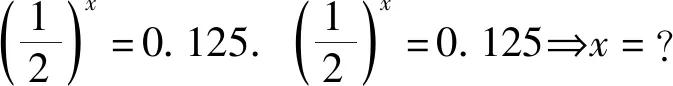
设计意图好的开端是成功的一半,情境引入对后续的学习有重要的作用.这个情境融入数学文化,体现了学习对数的人文价值,让学生觉得亲切自然,然后根据题意,设未知数,列出方程,思考如何表示x,激发其对学习对数的兴趣,抓住了学生认识新知的逻辑起点,渗透方程、转化等思想,发展学生数学抽象和数学建模素养.
由问题1引出对数的定义:一般地,如果ax=N(a>0,a≠1),那么数x叫做以a为底N的对数,记作x=logaN,其中a叫做对数的底数,N叫做真数.此时学生往往对概念的理解还是不到位的,仅仅是了解对数式与指数式可以互化:ab=N⟺b=logaN.于是提出问题2.
问题2(1)为什么对数的定义中要求底数a>0且a≠1?(2)是否是所有的实数都有对数呢?
设计意图让学生明确对数式与指数式形式的区别,a,b和N位置的不同,在互化中发展逻辑推理与数学运算素养.
问题3
1.将下列指数式写成对数式:
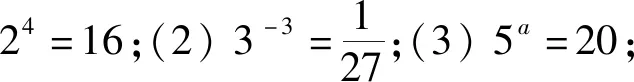
2.将下列对数式写成指数式:
(1)log5125=3;(2)log0.58=-3;
(3)log10a=1.1.
设计意图让学生进一步熟悉对数式与指数式的相互转化,加深对对数概念的理解.并让学生指出对数式与指数式互化时应注意哪些问题,增强运算、观察、类比、交流等活动,培养学生严谨的思维品质,发展数学运算素养.
问题4求下列各式的值:
(1)log31=;(2)lg1=;
(3)log0.51=;(4)ln1=.
思考:你发现了什么?
问题5求下列各式的值:
(1)log33=;(2)lg10=;
(3)log0.50.5=;(4)lne=.
思考:你发现了什么?
设计意图问题4和5让学生自己得出“1的对数等于零”和“底数的对数等于1”这两个结论,从而更好地理解和掌握对数的性质,培养学生类比、分析、归纳的能力,积累数学基本活动经验,在学生归纳小结中发展了学生数学运算和逻辑推理素养.
问题6求下列各式的值:
(1)2log23=;(2)6log60.3=;
(3)0.2log0.20.3=.
思考:你发现了什么?
问题7求下列各式的值:
(1)log334=;(2)log0.90.95=;
(3)lne0.1=.
思考:你发现了什么?
设计意图问题6和7让学生自己推导得出结论alogaN=N及logaaN=N,在归纳中发展学生数学抽象和逻辑推理素养.
以上7个问题形成的“问题串”,让学生在独立思考、自主探究、合作交流等学习方式下,经历了实质性思维参与过程, 提升了学生的素养.
2.3 整体把握教学内容,推动核心素养的生长点
学生数学学科核心素养水平的达成不是一蹴而就的,具有阶段性、连续性、整合性等特点.教师应理解不同数学学科核心素养水平的具体要求,不仅关注每一节课的教学目标,更要关注主题、单元的教学目标.所以,整体把握教学内容对促进数学学科核心素养连续性和阶段性发展具有重要意义.
案例3数列的概念
片断1概念引入
教师写出一组数:1,1,2,3,5,8,13,21,34,55,89,…引导同学们一起来观察这组数的奇妙属性.
生1:从第三项开始,每一项是前两项的和.
生2:从第二项开始,每个奇数项的平方都比前后两项之积多1.
生3:从第二项开始,每个偶数项的平方都比前后两项之积少1.
生4:随着这一列数项数的增加,前一项与后一项之比越逼近黄金分割0.6180339887……
师:这组数是意大利数学家斐波那契发现的,因此这个数列又叫斐波那契数列.
然后,教师通过这个例子引出数列及相关概念.
设计意图利用数学文化引入,介绍数学家或数学史,可提高学生的学习兴趣和求知欲望,通过数学文化的领航,抽象出数列的知识框架,明确了数列的学习目标,为这节课乃至整个单元的学习做好铺垫.渗透数学文化,可以帮助学生打开一扇窗,引导学生去探索数学美的世界.
片断2概念理解
师:由数列的概念可以发现,在数列中由项的序号可得对应项,即对于每一个序号n,都有唯一的项an与之对应,你能从中得到什么启示?
生5:数列是函数.
师:很好,所以数列也是种函数,数列与函数有何联系和区别?
生6:数列是种特殊的函数,特殊在定义域是正整数,图象是一些孤立的点.
师:通项公式可以看成数列的函数解析式.利用一个数列的通项公式,你能确定这个数列哪些方面的性质?
生7:写出该数列的某些项.
生8:求该数列中的任意一项或判断某个数是否为该数列中的项.
生9:判断该数列的增减性及是有穷数列还是无穷数列.
生10: 求该数列最大最小项.
师:你是用什么方法得出以上的性质?
生11:列表、图象、通项公式等.
设计意图了解数列是一种特殊函数,这是数列概念的核心,学生知道了这点后,在今后研究数列时,就懂得可以类比研究函数的方法,研究对象从函数到数列是变了,但“研究套路”不变,思想方法不变!这就是数学基本思想、数学基本活动经验的力量!由此发展了学生的数学抽象素养.指导学生从列表、图象、通项公式等方法表示数列,与函数的表示方法进行类比,进一步认识数列的函数本质,发展了学生的直观想象素养.
2.4 深度融合信息技术,发展核心素养的增长点
案例4离心率的概念
离心率的概念抽象性强,直接引入较为生硬,学生不易掌握.圆锥曲线的第二定义是围绕着离心率展开的,深入理解离心率的概念是掌握圆锥曲线性质的基础.教学过程中,教师可以借助信息技术进行概念的引入,操作流程为教师提出问题→学生探究→信息技术验证.具体过程如下:
教师打开几何画板,引导学生观察椭圆不同的形状,有的“扁”,有的“圆”.教师提出问题1:我们该用一个什么样的量来刻画椭圆的“扁圆”程度?这个问题对于学生有较大的挑战性,一般较难回答.此时,教师可以启发学生回顾用定长画椭圆的过程与哪些基本量有关,从而猜测椭圆的“扁圆”程度与椭圆的哪些基本量有关?
生:椭圆的“扁圆”程度与基本量a与c有关.
师:打开几何画板,当a不变时,改变c的大小,椭圆的“扁圆”程度发生变化,说明椭圆的“扁圆”程度与c有关;当c不变时,改变a的大小,椭圆的“扁圆”程度发生变化,由此说明椭圆的“扁圆”程度与a有关.综上说明椭圆的“扁圆”程度与a、c都有关.
问题2:怎样用a、c来刻画椭圆的“扁圆”程度.
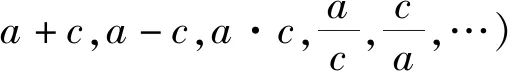
师:打开几何画板,如图8所示,先拖动点Q,确定a+c的值,确定后,再拖动点P,拖动过程中,a、c的值在变化,但a+c的值保持不变,椭圆的“扁圆”程度发生变化,由此说明不能用a+c来刻画椭圆的“扁圆”程度.
如图9所示,先拖动点E,确定a-c的值,确定后,再拖动点A,拖动过程中,a、c的值在变化,但a-c的值保持不变,椭圆的“扁圆”程度发生变化,由此说明不能用a-c来刻画椭圆的“扁圆”程度.
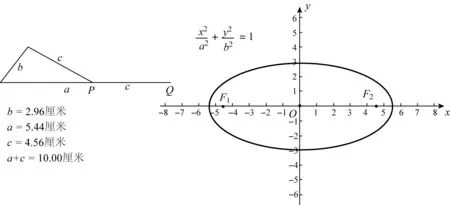
图8
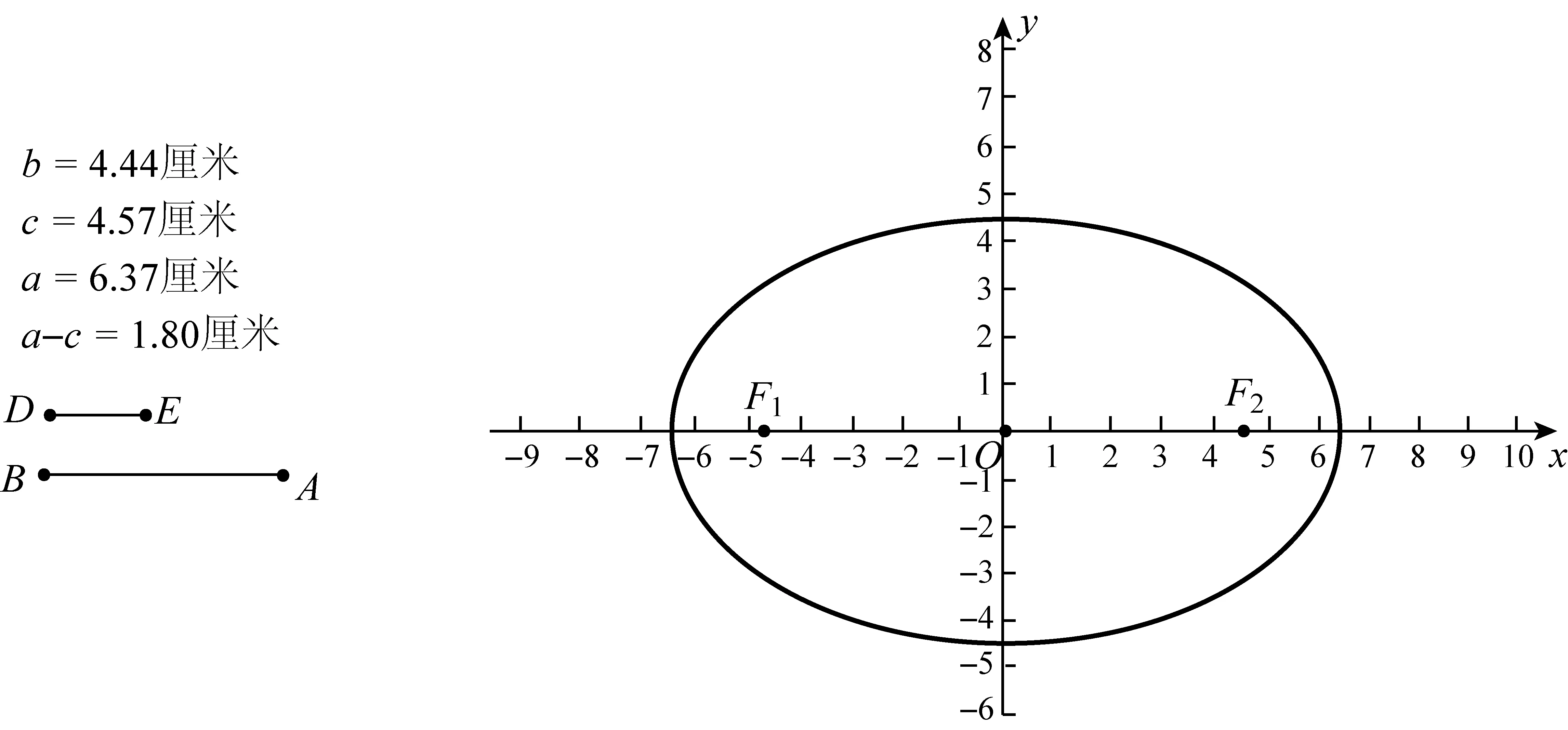
图9
如图10所示,先拖动点P,确定a·c的值,确定后,再拖动点Q,拖动过程中,a、c的值在变化,但a·c的值保持不变,椭圆的“扁圆”程度发生变化,由此说明不能用a·c来刻画椭圆的“扁圆”程度.
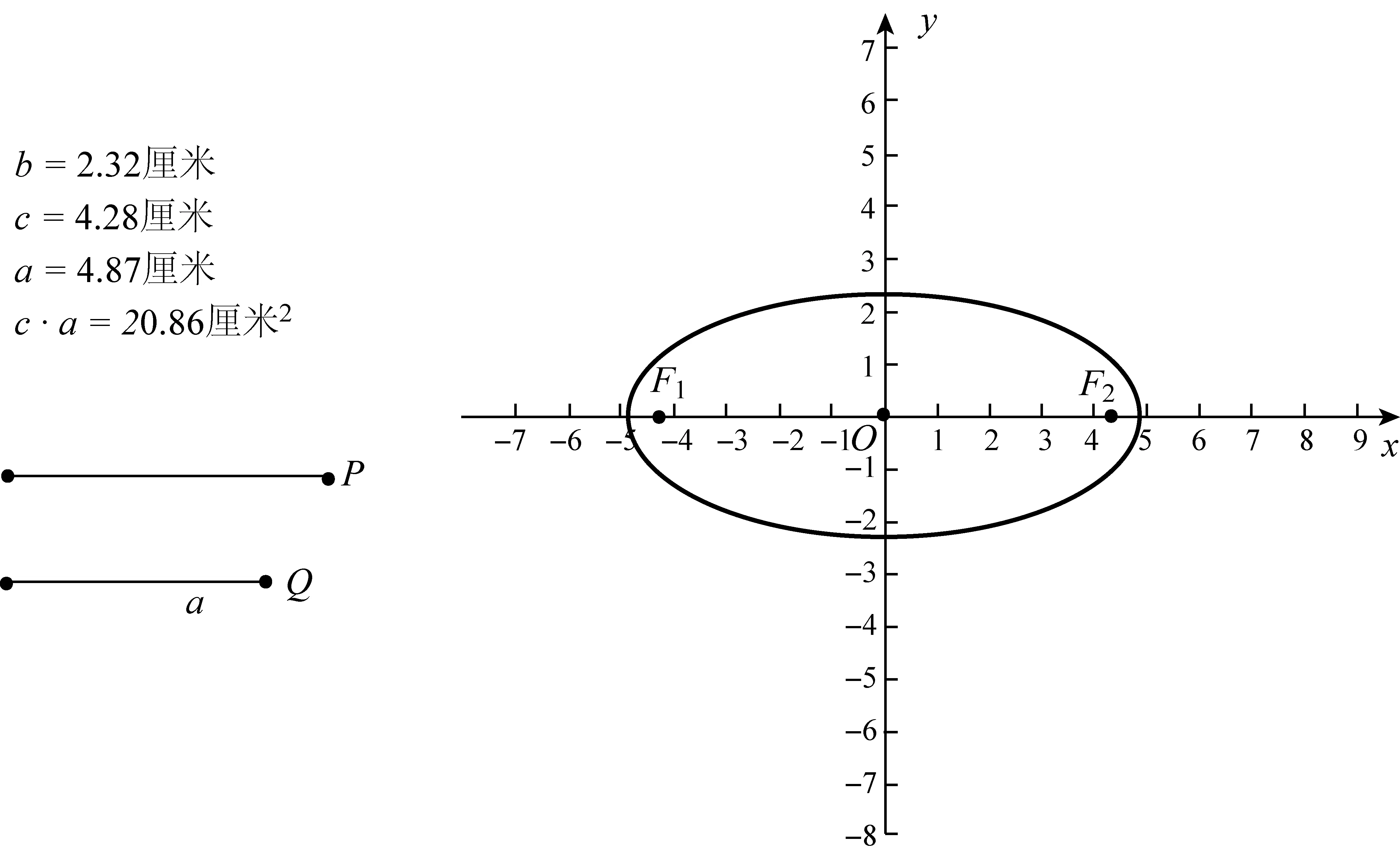
图10
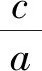
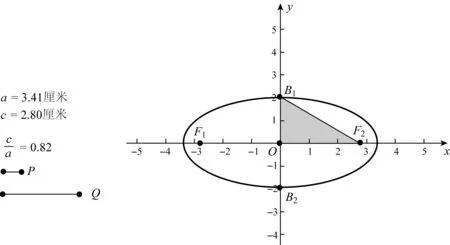
图11
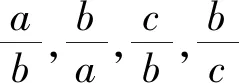
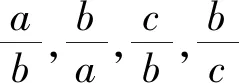
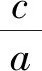
设计意图学生绘制椭圆图形过程中,由直观感知自然地分析椭圆的“扁圆”程度是由哪些量刻画.根据学生思考及交流提出的探究方案,教师提出问题并引导学生探究猜测,结合几何画板加强直观感受并进行验证,通过这一系列过程使学生感受到研究问题的方法,特别是多变量问题该如何处理,即先猜后证的方法,感受到自己探究的价值,从而体会定义生成的完美,至此得出离心率这一概念.探究的过程使学生明白数学中的任何发现都并非“一蹴而就”的,需要锲而不舍的钻研精神.
对概念进行研究,教学中应从本质上理解,从而达到触类旁通的效果.离心率作为刻画圆锥曲线性质的核心概念,是运用数形结合的思想方法来研究圆锥曲线.深入剖析离心率的探究历程对学生的数学抽象、直观想象以及逻辑推理等数学核心素养的培养具有重大的意义.在探究的过程中,充分地融合了信息技术,利用几何画板验证学生探究的几个方案,实现了信息技术增大课堂容量的功能;在椭圆的“扁圆”程度变化的过程中,实现了信息技术“抽象问题具体化”、“隐性问题显性化”、“静态问题动态化”的功能,循序渐进地、有目的性地探究数学概念的内涵,解析它们在数学知识结构中的相互关联,提高学生的学习能力与数学能力,达到对学生关键能力培养的目标.
3 写在最后
李邦河院士说过:“数学根本是玩概念的,不是玩技巧的,技巧不足道也!”数学概念是导出全部数学定理、法则的逻辑基础,数学概念是相互联系、由简到繁形成学科体系.数学概念不仅是建立理论系统的中心环节,同时也是解决问题的前提.因此,概念教学是数学基础知识和基本技能教学的核心,而在概念教学中渗入核心素养,将有助于学生以后相关内容的学习,对后续数学的学习也起到重要的作用.

