欧拉不等式的一个加强的改进

张青山

(四川职业技术学院应用数学与经济系 629000)

文[1]将欧拉不等式加强为：

定理1在三角形ABC中，外接圆半径R，内切圆半径r，则(∑表示循环和)

(1)

文[2]将定理1改进为：

定理2在三角形ABC中，外接圆半径R，内切圆半径r，则

(2)

我们发现不等式

成立，这是由于

故设想将不等式(2)改进为

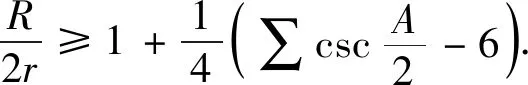
定理3在三角形ABC中，外接圆半径R，内切圆半径r，则

(3)

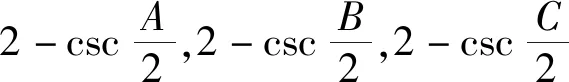
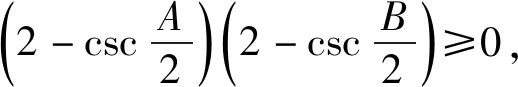
那么

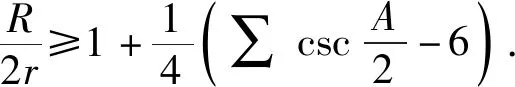
记三角形ABC的内心为I，

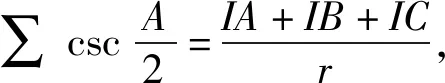
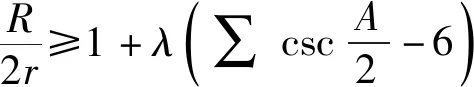
令AB=AC,BC→0，

注1

2(R+r)≥IA+IB+IC.

(4)

同理有

那么就得出不等式(4)的一个等价结论：

(5)

注2运用上面证明中的基本数学事实，可以简捷地证明一些不等式，如：

定理4在三角形ABC中，恒有(∏表示循环积)

(6)

(7)

我们仅证明(6)式，将(7)式的证明留给读者.

等价于

由(6)式可知

即

就可以得到欧拉不等式的又一个加强：

(8)