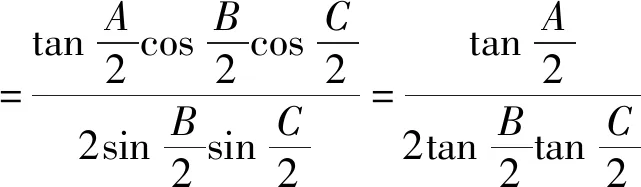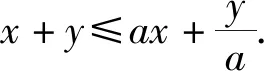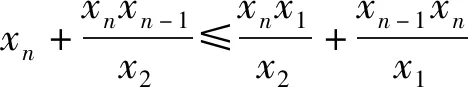数学问题解答
2019年8月号问题解答
(解答由问题提供人给出)

(浙江省富阳二中 许康华 311400)
证明将n表示成p进制形式,即令
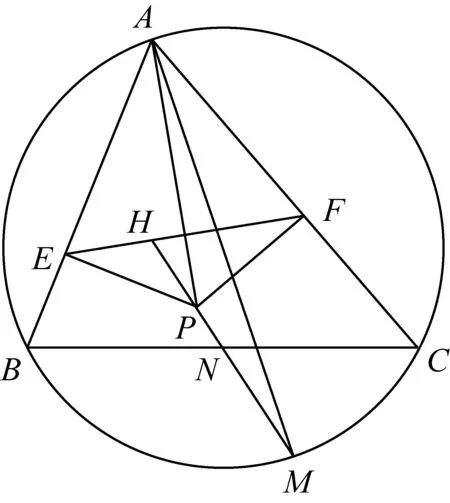
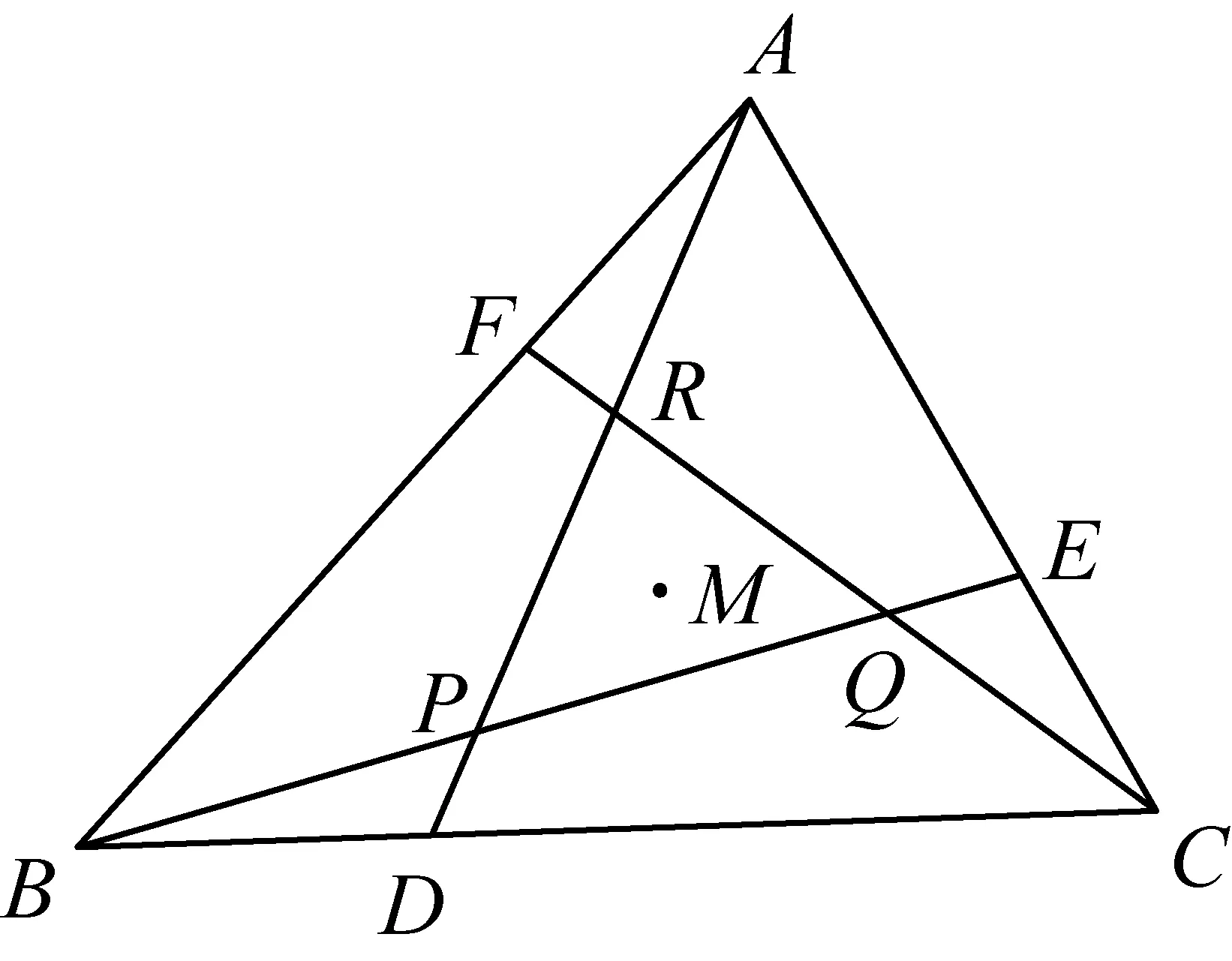
n=nkpk+nk-1pk-1+…+n1p+n0,(0≤ni (1) 同样,可令 n=mlql+ml-1ql-1+…+m1q+m0,(0≤mi (2) 若存在满足题意的常数a,则由(1),(2)得 (3) 所以有 (4) 因为n≥pk,n≥ql,所以k≤logpn,l≤logqn, ≤a(p-1)q(l+1)+(q-1)p(k+1) ≤a(p-1)q(logqn+1)+(q-1)p(logpn+1). 若(p-1)a-(q-1)≠0, 则任取0<ε<|(p-1)a-(q-1)|, 存在一个正整数N,当n>N时,必有 这与(4)式矛盾. 所以,此时使得(4)式成立的正整数n只有有限多个,与题意不符. 综上知,如果存在正常数a符合题意, 即n的p进制表示与它的q进制表示的数码和相等. 2497已知:如图,在线段AB中垂线上取两点C、D(不是AB中点).直线AD与BC相交于点E,直线BD与AC相交于点F.过A作AE的垂线,过B作BC的垂线,这两条垂线相交于点X.求证:∠CXF=∠DXE. (重庆市长寿龙溪中学 吴 波 401249) 证明因为∠XAE=∠XBE=90°, 所以X、A、E、B四点共圆. 设所共之圆为⊙O,圆心O在斜边XE上. 又CD垂直平分⊙O的弦AB, 所以圆心O也在CD上, 因此直线CD与XE的交点即是圆心O. 如图,由此可作出⊙O. 由对称性,点F也在⊙O上. 作X关于CD的对称点X', 连接XX'、BX'、DX'. 由对称性知 ∠X'BD=∠XAD=90°. 而∠XBE=90°,所以∠XBX'=∠CBD. 因AB⊥CD,XB⊥BC,则∠XBA=∠BCD. 而由对称性知XX'⊥CD, 因此XX'//AB.则∠XBA=∠BXX', 所以∠BXX'=∠BCD, 又∠X'BD=∠XAD=90°, 所以△BDX'∽△BCX,有∠BXC=∠BX'D. 又由对称性知 ∠BX'D=∠AXD, 所以∠AXD=∠BXC, 所以∠AXC=∠BXD. 又易知EF//AB,所以AF=BE, 有∠AXF=∠BXE, 由此即得 ∠CXF=∠DXE. 2498设△ABC三边长,三个旁切圆半径分别为a,b,c,ra,rb,rc,则有 (天津水运高级技工学校 黄兆麟 300456) 由旁切圆半径公式及正弦定理,可得 那么就有 从而就有 以上证明用到了熟知的公式 2499如图,O为△ABC内一点,AO平分∠BAC.过点A的直线MN∥BC,射线BO分别交AC,MN于点P,M,射线CO分别交AB,MN于点Q,N.求证:AB=AC的充要条件是PM=QN. (江苏省兴化市第一中学 张 俊 225700) 证明(必要性) 因为AB=AC,AO平分∠BAC, 所以∠ABC=∠ACB,△ABO≌△ACO, 所以BO=CO,∠ABO=∠ACO, 又∠BOQ=∠COP, 所以△BOQ≌△COP,所以OP=OQ. 又由MN∥BC,BO=CO, 知∠M=∠OBC=∠OCB=∠N, 所以OM=ON. 故PM=OM-OP=ON-OQ=QN. (充分性) 如果AB≠AC,不妨假设AB 在AC上取点D使AD=AB, 联结DO,延长AO交BC于F. 因为AO平分∠BAC,所以△ABO≌△ADO. 所以∠ODC>∠AOD=∠AOB>∠AFB>∠ACB>∠ACO, 所以CO>OD=BO,所以∠OBC>∠OCB, 又MN∥BC, 所以∠M=∠OBC>∠OCB=∠N 所以ON>OM, 所以CN=CO+ON>BO+OM=BM. 因为PM=QN, 所以BM-PM 因为∠ABO=∠ADO>∠ACO, 故可在线段OQ上找点E使∠EBO=∠ACO, 所以E,B,C,P四点共圆, 所以∠BEC=∠BPC. 所以∠EBC=∠EBO+∠OBC >∠ACO+∠OCB=∠PCB, 因为EC,BP分别为圆周角∠EBC,∠PCB所对的弦, 所以EC>BP,又CQ>EC, 所以CQ>BP. (2) (1)与(2)矛盾说明假设不成立,故AB=AC. 2500设n是正整数,且n≥3,证明:对正实数x1≤x2≤…≤xn,有不等式 ≥x1+x2+…+xn. (上海市七宝中学 李佳伟 201101) 事实上,由ax≤x≤y得到(1-a)(y-ax)≥0, 即a2x+y≥ax+ay, 代入得 上式对i=1,2,…,n-2求和,即得到 x1+x2+…+xn-2+ ① ② 由①+②即得到原不等式成立. 2019年9月号问题 (来稿请注明出处——编者) 2501设△ABC的三内角A,B,C所对的三边长分别为a,b,c,三角形的面积△,求证: (1) 当且仅当△ABC为等边三角形时式中等号成立. (河南质量工程职业学院 李永利 467000) 2502设AM为锐角三角形ABC的外接圆直径,N为边BC的中点,P为∠BAC的平分线AP与直线MN的交点,E,F分别为点P在两边AB和AC上的射影,证明:直线MN与EF的交点H是△ABC的垂心. (河南辉县一中 贺基军 453600) 2503△ABC中,a,b,c分别表示三角形三边长,I为△ABC的内心,则 (浙江省永康市第六中学 吕永军 321300) 2504已知a,b,c>0,abc=1,求证: (河南省南阳师范学院软件学院 李居之 孙文雪 473061) 2505如图,△ABC中,D,E,F分别是边BC,CA,AB上的点,且BD=mBC,CE=mCA,AF=mAB,0 求证:△ABC与△PQR的重心重合. (湖北省公安县第一中学 杨先义 434300)