一个无理分式不等式猜想的证明①
2019-10-22 10:13刘春平
数学通报 2019年9期
刘春平
(扬州大学数学科学学院 225002 )
《数学通报》2016年9月问题2325[1]为:
设x,y是满足xy=1的正数,λ≥0,求证:
最近,文[2]从指数与项数人手,将问题2325进行推广得到了三个定理,其中定理3为:
设x,y>0,xy=1,m≥2,m为整数,λ≥0,有
在考虑将定理3再推广至n元时,文[2]作者“倾向于结论成立但久思不得证法”[2],故提出了如下
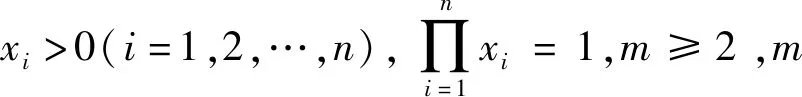
下面,本文利用变量变换和Jensen不等式给出上述猜想的证明.

对f(θ)求导得
当m≥2,m为整数,λ≥ 0 时,f″(θ)>0,
故f(θ)在(-,+)上为凸函数,
根据Jensen不等式有
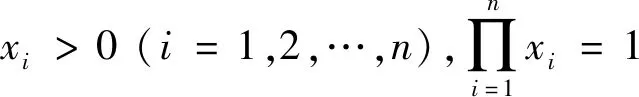
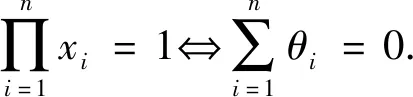
即
文[2]猜想得证.
猜你喜欢
语数外学习·高中版上旬(2022年5期)2022-07-11
天府数学(2020年3期)2020-09-10
河北理科教学研究(2020年1期)2020-07-24
儿童故事画报(2019年5期)2019-05-26
作文·初中版(2017年4期)2017-04-18
读与写·下旬刊(2016年5期)2016-06-12
环球时报(2014-01-06)2014-01-06
中学数学研究(2008年3期)2008-12-09

