高中数学建模能力训练——案例教学中提升数学素养

王志俊 韩 苗 邵 虎 周圣武

(中国矿业大学数学学院 221116)

1 高中数学建模的意义

高冷的数学在以一种高度抽象的形式存在的同时, 又是各门科学的基础, 它在自然、工程、人文、社会等方面都发挥着重要的作用. 数学要走向应用, 就必须在数学与应用之间架设一个桥梁[1]. 将实际问题首先转化为相应的数学问题, 即数学模型, 然后对这个数学模型进行求解, 最后利用其结果去解决原先的实际问题, 这个过程就称为数学建模. 数学建模是数学走向应用的必经之路.

高中数学建模活动通常以小组为单位进行, 这有利于培养学生的集体意识和分工协作精神. 活动题目大多来自工程实际和社会生活, 没有固定的范围, 这有利于提高学生的文献检索能力和自学能力. 活动所要解决的问题除了应用数学知识外, 通常还要用到其它相关专业知识、科学计算软件等, 这有利于发展学生不同知识的交叉融合能力与计算机编程能力. 活动最终提交的作品一般是研究报告或小论文, 这有利于提升学生写作与文字表述的能力. 总之, 高中数学建模活动能够增强学生的创新意识和科学精神, 提升学生的数学综合素质.

2 现状分析

在《普通高中数学课程标准(2017年版)》[2]中, 作为数学学科的核心素养之一, 数学建模与数学抽象、逻辑推理、直观想象、数学运算、数据分析等构成了一个有机的整体. 强调数学与生活以及其他学科的联系, 提升高中生应用数学解决实际问题的能力已经成为普通高中数学课程的基本理念之一. 许多学者在中学数学建模方面做了理论研究和大胆尝试. 罗琼和廖运章[3]从数学建模的课程定位、实施策略和信息通信技术在数学建模中的应用等方面介绍了新加坡在数学建模教育中的情况；陈呈和王金才[4]、钱月凤[5]分别对中新和中德在数学建模的课程标准、教材处理、教学策略、评价方式等方面进行了详尽的比较；李明振和喻平[6]、赵思林和崔静静[7]分别从数学建模的背景解析和数学建模对中学生数学学习的影响角度为我们揭示了课程实施过程中存在的问题, 并初步探索了解决问题的有效对策；周龙虎和刘师妤[8]、刘丹[9]分别以不等式模型和函数模型为例探求了数学建模过程中的教学思路和教学方法.特别需要指出的是, 张思明和喻运星[10]为我们提供了12个不同类型难度适中的中学数学建模素材和案例, 并且设计了一种新颖的“使用情节”引导学生独立思考、动手实践、启发反思.

自上世纪80年代以来, 在应用数学工作者的不懈努力下, 数学建模在高等教育领域取得了丰硕的成果, 数学建模课程(含数学实验)及其理论研究在高校开展得如火如荼；以全国大学生数学建模竞赛为代表的各类实践活动更是将数学建模推向了高潮, 促进了数学与工业之间的深度融合, 为各个领域内的许多具体问题提供了切实可行的解决方案.

数学建模不仅仅是一种解决问题的“套路”, 更是一种思维方式, 高中生数学建模核心素养水平的高低将直接影响他们未来接受高等数学教育的过程. 与国内高校遍地开花的景象形成对比的是, 数学建模在普通高中的开展情况并不尽如人意, 部分高中教师进行数学建模课程教学的意愿不高, 部分学生也不愿在数学建模学习上花费太多时间, 这样普通高中组织学生参与数学建模竞赛活动的积极性也受到很大影响. 显然造成这一现象的原因有很多. 数学建模的特点决定了仅仅从理论上学习数学建模的思想和方法, 而不借助于一些案例和素材去实践是不符合科学规律的, 我们认为缺乏适合高中教师和学生参加数学建模活动的案例和素材是其中原因之一. 本文正是希望能够在此方面做一点工作：以课标中数学建模核心素养的水平划分标准为依据,将五一数学建模竞赛中的部分赛题凝练成适合高中的数学建模案例和素材, 供开展数学建模活动时参考使用, 并期待与高中数学同行交流.

3 案例及分析

高中数学的课程包括必修课程、选择性必修课程和选修课程三大结构. 根据课程标准, 必修课程和选择性必修课程均要求学生以课题研究的形式开展数学建模主题的活动, 经历数学建模的全过程, 撰写研究报告并进行评价. 选修课程共分五类供学生根据个人志趣自主选择, 其中A,B,C类课程均在不同程度上以数学建模专题作为课程内容之一.A类课程虽然没有明确数学建模专题, 但是要学习以线性回归为代表的应用统计类模型；B类课程侧重于结合实际问题建立一些基本的函数模型(如线性模型、二次曲线模型、指数函数模型等)；而C类课程则更侧重于一些基于数学表达的经济模型和社会模型.

在对上述三类课程数学建模主题的侧重点进行分析后,我们以①宜居城市评价, ②标枪尺寸问题, ③景区游览路线设计作为案例, 分别从应用统计类模型、函数类模型和线性规划模型的角度进行分析,展示数学建模思想和方法, 反映数学建模对学生数学能力发展和素养提高的影响.

3.1 宜居城市评价

案例建设宜居城市是现阶段我国城市发展的重要目标, 是政府和城市居民密切关注的焦点. 一座宜居的城市不仅应具备物质丰足、生活便利等条件, 而且应注重人们的切身感受. ①请查阅相关资料和数据, 筛选评价宜居城市的主要指标, 在阐述这些指标合理性的基础上建立评价宜居城市的数学模型. ②选择6-10个规模相当的城市, 利用所建模型对这些城市进行合理研究, 并给出城市宜居排名.

诊断分析该问题是数学建模综合评价问题. 问题①首先需要查找资料选择宜居城市评价指标, 根据物质丰足、生活便利、切身感受等信息, 我们发现经济发展、生态环境、教育文化、交通医疗等是几个比较重要的影响因素. 通过数据收集、整理、分析, 可以将这些因素细化确定出若干指标. 对这些指标进行加权综合是建立宜居城市评价数学模型的关键, 而权重的赋值科学与否对评价结果的合理性起着至关重要的作用. 为此, 我们应根据自己的知识水平选择主观赋权或客观赋权进行综合评价, 其中主观赋权可以采用层次分析、综合评分、指数加权等方法根据经验进行主观判断来确定权重, 客观赋权则可以采用线性回归、主成分分析、变异系数等方法根据各项指标的变异系数或者指标之间的相关关系来确定权重. 对于问题②, 我们首先需要查找与上述指标密切相关的所选城市的数据, 笔者认为各城市的统计年鉴是能够全面系统反映该市国民经济和社会发展各方面情况的资料, 具有一定的权威性, 值得借鉴使用. 然后, 我们可以将这些查找到的数据整理分类(比如采用最小二乘法进行聚类分析)并对应至问题①中的各项指标. 最后, 将各项指标值代入到建立的模型中, 借助于统计软件(如SPSS)进行数值计算, 并根据结果对所选城市宜居性排序.

小结通过对本案例分析我们发现, 该问题属于数据分析, 统计建模问题. 该案例的解决可以让学生经历较为系统的数据处理过程, 理解统计问题的建模思路, 并从中学习到数据分析的方法, 体验常用统计软件的使用. 这样, 学生通过数据认识事物的思维品质得以形成, 基于应用统计表达现实问题的意识得以加强, 数据分析的核心素养得以提升.

3.2 标枪尺寸问题

案例标枪的投掷是一项历史悠久的田径比赛项目. 国家标准 GB/T 22765-2008-标枪规定了标枪的分类和比赛标枪的基本参数. 表1是某型比赛标枪的测量尺寸数据, 请估算该型标枪沿标枪中轴线剖面面积、标枪表面积和标枪形心的位置, 其中形心是指标枪沿中轴线剖面图形的几何中心.

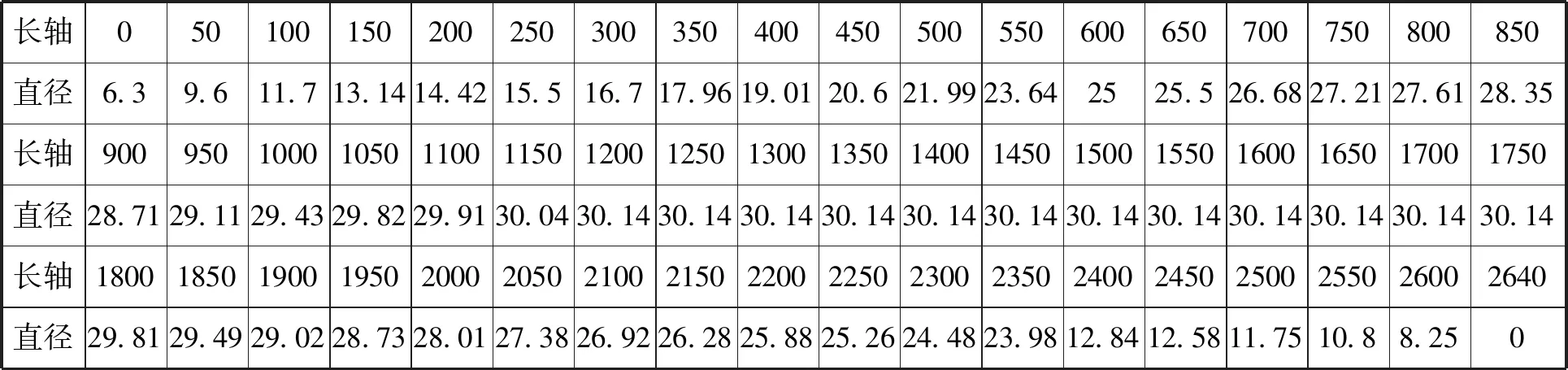
表1 某型标枪测量尺寸表(单位mm)

诊断分析根据该国家标准中的标枪示意图, 我们相信学生对中轴线剖面和表面的理解是明确的.这两个面的面积可以用下面两种方法求得. 我们可以依据尺寸表将标枪分成若干小段, 每一小段的剖面和表面就可以分别近似成一个梯形和一个圆台的侧面, 因此可以用初等数学的方法通过累加得到剖面面积和表面积的近似值. 更准确一点的, 我们可以将标枪放至坐标系中, 借助于Matlab拟合工具箱对尺寸数据进行拟合处理, 将标枪剖面轮廓用多项式函数曲线去近似, 然后利用函数积分计算得到剖面面积和表面积. 课标中虽然有几何对象、位置关系等内容, 但对于形心并无明确说明, 在寻找标枪形心位置之前, 我们需要准确理解形心的概念, 最好能够理解物体的形心、质心和重心之间的联系和区别. 由于尺寸表给出的是长轴上某位置的直径, 我们可以假设标枪的截面是圆面, 这样标枪的形心一定位于中轴线上. 对于形心位置的确定, 我们也可以借鉴上述两种处理方法, 借助于梯形、离散点的形心公式和Matlab求形心方法类似得到.

小结通过对本案例分析我们发现, 该问题既可以归结为几何问题, 根据直观图形直接计算得出近似结果, 又可以归结为函数模型, 拟合后利用微积分的方法探索出更好的解决方案. 另外, 该问题还可以促使学生主动去获得新的知识(比如梯形的形心公式), 寻求新的方法(如拟合工具箱). 不仅如此, 该案例的解决促进了学生数形结合、分析抽象、软件使用等能力的发展, 提升了直观想象、数学运算和数学建模素养.

3.3 景区游览路线设计

案例某景区共有8个旅游景点(A-H), 任意两个景点之间的最短距离如表2所示. ①请找出从A景点出发, 经过B-G所有景点至少1次, 最终到达H景点距离最短的游览路线, 并计算该路线的长度. ②游客在景区停留的时间由景点间步行时间、等待时间和景点游览时间组成, 其中各景点游览时间如表3所示. 某游客计划以2 km/h的步行速度12:00从A景点出发, 17:30从H景点离开. 请为该游客设计一条能游览完全部景点且游览总时间最长的路线, 并计算出在每个景点的游览时间.

表2 景点间最短距离(单位：m)

表3 各景点游览时间(min)

诊断分析本案例是在给定条件下规划游览路线的问题, 重点研究分析不同情况下的游览路线设计, 通过建立线性规划模型进行求解. 对于问题①, 题目要求至少经过每个景点一次情况下的最短路径, 该问题是一个典型的最短路问题. 在含8个顶点的无向图中求两顶点之间的最短路线, 建立整数线性规划模型, 应用 Dijkstra 算法或遗传算法求解此问题, 得到按总路径从短到长的各种不同路线. 另外, 我们还可以将景点间的距离看成是一个8阶矩阵, 通过矩阵的变换求得最短路线. 例如, 当从景点A出发到景点B时, 此时不能再到其他景点, 可以将矩阵的第A行和第B列去掉. 问题②是在问题①的基础上增加了景点开放时间和每个景点游览时长限制等约束条件, 目标是找出总游览时间最长的路线. 考虑到步行速度一定, 要使总游览时间最长, 则步行时间和等待时间(注：景点D每整点开放, 可能会产生等待时间)之和最短. 结合表2中各景点游览时间的要求, 增加约束条件, 可以通过构建组合优化后的线性规划模型进行求解.

小结通过对本案例分析我们发现, 若要保证整个游览路线的距离最短, 每个景点只能经过一次, 利用这一约束条件建立整数线性规划模型有利于提高学生的分析能力和优化能力；其次, 8个景点的组合结果较多, 完全枚举费时且耗力, 因此需借助一定的数学软件对模型加以求解, 这能够提高学生对数学软件的使用能力；最后, 矩阵的概念在课标中已有初步涉及, 本案例中的矩阵有助于加强学生对图形的抽象能力, 矩阵变换有助于加强对几何和代数的理解.

4 数学建模素材

最后, 我们从五一数学建模竞赛历年赛题中凝练出4道题目素材, 其中素材1可以考虑使用统计类模型解决,素材2—4则更适合使用各种线性规划或组合优化模型.

素材1 高中生体质健康评价

《国家学生体质健康标准》是测量学生体质健康状况和锻炼效果的评价标准. 该标准中测试指标会随组别的不同而发生一定的变化, 但身高、体重、肺活量、50米跑和坐位体前屈是所有组别的共性指标. 在对这些指标进行测试时, 个别测量数据可能存在误差, 不能反映真实水平. ①请分别分析体重和50米跑对体质健康的影响；②搜集你所在班级(或年级)中男生(或女生)50米跑的体测数据, 建立数学模型, 检验数据的准确性, 找出其中可能存在误差的数据, 并说明理由.

素材2 木材切割方案设计

家具厂在家具加工过程中需要使用切割工具对整块木板进行切割以生产出不同规格的产品. 假设整块木板的规格是3000*1500(单位：mm), 产品P1和P2的规格分别是373*201和406*229. 请在不计木板厚度和割缝宽度的情况下思考并分析如下问题：①假设在一块木板上切割产品P1, 请给出木板利用率最高(即剩余木板面积最小)的切割方案, 并计算P1的数量；②假设在一块木板上同时切割产品P1和P2, 请给出按照木板利用率由高到低排序的前3种切割方案, 并计算P1和P2的数量；③假设要生产P1产品774件, P2产品1623件, 请问最少需要多少块木板？

素材3 行程优化设计

某背包客计划从徐州出发乘火车(含高铁, 火车票价以中国铁路12306网站公布为准)到常州、青岛、北京、洛阳、黄山、武汉、西安、九江等八个城市旅游, 最后回到徐州. ①请为背包客设计游览全部八个城市且火车票费用最省的行程表. ②假设该背包客只预算了2000元的火车票费用, 请为背包客设计行程表使得旅游城市尽可能多.

素材4 救护车位置优化设计

某城市的紧急服务协调机构负责安排全市三辆救护车的位置, 目的是最大限度地提高紧急呼叫的居民数量, 可在8 min内到达指定地点. 该城市划分为6个区, 从一个区到另一个区所需的平均时间如表5, 请确定三辆救护车的位置使得在120电话打出8 min内赶到救援地点所覆盖的人数最多.

表4 区域人口(单位：万人)

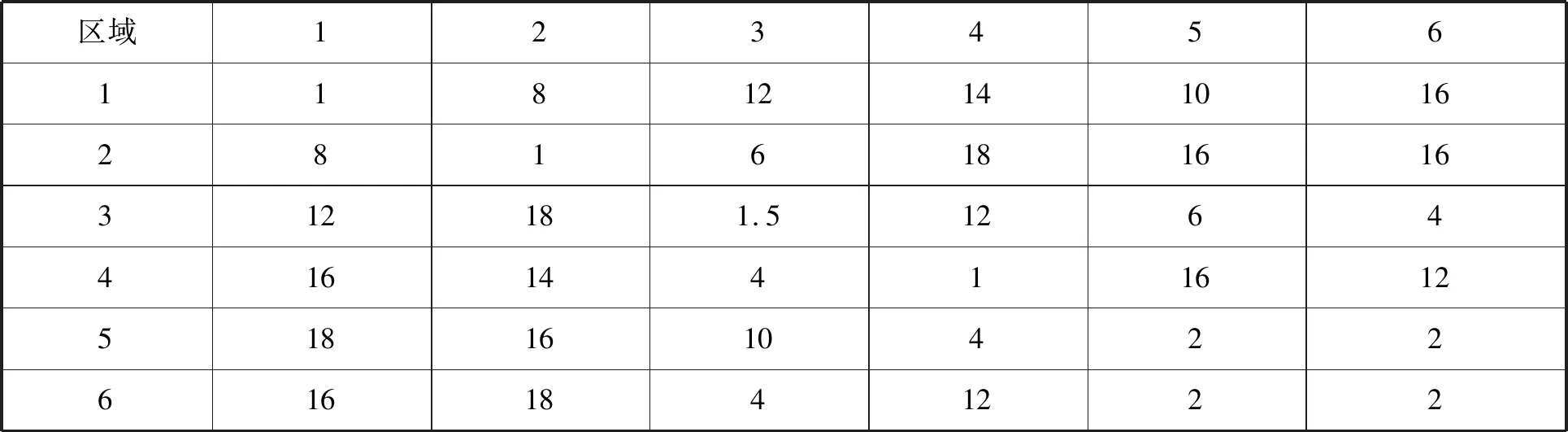
表5 各个区域间平均路途时间(min)