以圆周角定理为例谈中考数学复习策略*

福建省厦门实验中学(361116) 刘云啟 黄耿跃

中考数学复习是学生掌握基础知识,形成基本技能,提升基本能力和基本思想的关键环节.而数学知识点繁多,知识点之间的联系庞杂,如何让学生在较短的时间内复习质量最大化,这就需要教师在中考数学复习策略上下功夫.笛卡尔在《方法论》中写道：“可以将要研究的复杂问题,尽量分解为多个比较简单的小问题,一个一个地分开解决.将这些小问题从简单到复杂排列,先从容易解决的问题着手.所有问题解决后,再综合起来检验,看是否完全,是否将问题彻底解决了”[1].笔者认为,紧扣中考考试大纲,以基础知识、基本技能、基本能力和基本思想构成的“四基”为复习路径,不仅能够较好地渗透笛卡尔著名的方法论准则,而且可以作为中考数学复习中比较有效的方式.本文以圆周角定理这一知识点为例,谈谈如何在中考数学复习中实践以上复习方式.

一、圆周角定理的基础知识

定理学习是培养学生思维能力的优质素材,创设思维的空间[2].圆周角定理中有两层意思,一层意思是“同弧所对的圆周角相等”,另一层意思是“一条弧所对的圆周角等于这条弧所对的圆心角的一半”.圆周角定理教学的实质就是挖掘揭示这两层意思的思维过程[3].

例1已知：如图1, 在⊙O 中,弧BC 所对的圆周角和圆心角分别是∠BAC、∠BOC.求证：∠BAC =

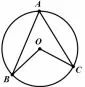
图1

评注例1 只是探究同弧所对圆周角和圆心角关系的一种情况,在复习教学时,教师应要求学生将其它两种情况表示出来.目的在于加深学生分类讨论的意识,加强学生识图作图的能力,渗透转化与化归的数学思想.虽然圆周角定理比较容易理解,但在复习基础知识时,不应急于练习,而应追根溯源,弄清楚推导圆周角定理的路径,吃透圆周角定理,知其所以然,也为提升基本技能做铺垫.

例2(2018年广东)同圆中,已知弧AB 所对的圆心角是100°,则弧AB 所对的圆周角是____.

变式题1同圆中,已知弧AB 所对的圆周角是100°,则弧AB 所对的圆心角是____.

评注考查的知识点：圆周角定理(圆周角的度数等于它所对弧上的圆心角度数的一半).虽然例2 及变式可以直接利用圆周角定理得出答案,但熟练得出答案的前提应基于例1 的追根溯源,建立起圆周角定理的强大根基,学生才能够适应在基本技能和基本能力方面的考查.

二、考查圆周角定理的基本技能

例3(2018年吉林, 13) 如图2,A,B,C,D 是⊙O 上的四个点,弧AB =弧BC, 若∠AOB = 58°, 则∠BDC =____度.

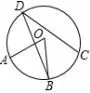
图2

评注上题考查了圆心角定理推论和圆周角定理知识,求解本题需要熟练掌握这两个知识点,并通过知识点间的联系进行技能叠加.学生形成圆周角定理的基本技能,有助于实现同类型题目的多题一解.我们给出例3 的变式题2.

变式题2(2018年广州, 7) 如图3,AB 是⊙O 的弦,OC ⊥AB,交⊙O 于点C,连接OA,OB,BC,若∠ABC = 20°,则∠AOB 的度数是( )

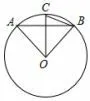
图3

A.40°B.50°C.70°D.80°

评注变式题2 是考查圆周角定理基本技能的进一步深化.除了涉及圆心角定理推论和圆周角定理,它还考查了垂径定理.

例4(2018年北京, 12) 如图4,点A,B,C,D 在⊙O 上, 弧CB = 弧CD, ∠CAD = 30°, ∠ACD = 50°, 则∠ADB =____.

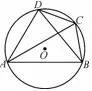
图4

评注与例3 不同,本题考查了圆周角与圆心角及其所对弧的关系、圆周角定理.但其中都涉及到圆周角定理,以圆周角定理为出发点,可以进行多个单一技能的叠加.

变式题3(2018年天津,21)已知AB 是⊙O 的直径,弦CD 与AB 相交,∠BAC =38°.

(1) 如图5,若D 为弧AB 的中点,求∠ABC 和∠ABD的大小;

(2) 如图6,过点D 作⊙O 的切线,与AB 的延长线交于点P,若DP//AC,求∠OCD 的大小.

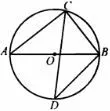
图5

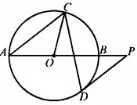
图6

评注变式题3 除了对例3 知识点的考查,还要求学生掌握平行线的性质定理、三角形的内角和定理,这就需要学生能够通过多个技能的叠加达到求解的目的.

上述试题均考查了圆周角定理,但每一道题目之间涉及的考点又有所不同.在教学中,培养学生进行题目之间的比较分析,有助于学生夯实知识点,建构知识点之间的联系,形成局部的知识网络,从而养成圆周角定理的基本技能,也为进一步提升基本能力打好基础.通过这四道试题的展示,可以清晰地发现例1 及其它两种情况的推导是十分有必要的,这有助于学生由单一技能向多技能叠加的转变,而熟练进行技能叠加的前提是对每一个知识点追根溯源的执着.当然,上述试题也有不同的解法,考查的知识点亦有所不同.

三、渗透在圆周角定理中的基本能力和基本思想

例5(2017年厦门市九年级期末质检试题,24)在⊙O中,点C 在劣弧AB 上,D 是弦AB 上的点,∠ACD =40°.

(1) 如图7,若⊙O 的半径为3,∠CDB =70°,求弧BC的长;

(2) 如图8, 若DC 的延长线上存在点P, 使得PD =PB,试探究∠ABC 与∠OBP 的数量关系,并加以证明.

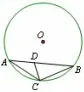
图7

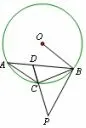
图8

评注(1)略.对(2)的思路可以从考查知识点、基本能力和基本思想分析,即从综合运用圆的性质、圆周角定理、等腰三角形性质、三角形中有关角的性质,到空间观念——利用半径等腰、同弧所对的圆心角与圆周角、三角形外角、等腰三角形等基本图形寻找已知量与未知量之间的简捷联系;推理能力、运算能力——根据设问,及图形特征,有向有序分析运算条件、探究运算方向,设计简捷的运算途径;再到化归与转化思想的渗透.

变式题4(2018年厦门市九年级期末质检试题,24)已知AB 是半圆O 的直径,M,N 是半圆上不与A, B 重合的两点,且点N 在弧MB 上.

(1) 如图9,MA = 6,MB = 8,∠NOB = 60°,求NB的长;

(2) 如图 10, 过点 M 作 MC ⊥ AB 于点C, P 是MN 的中点, 连接MB,NA,PC, 试探究∠MCP, ∠NAB,∠MBA 之间的数量关系,并证明.

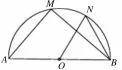
图9

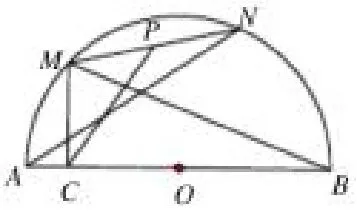
图10

评注从考查内容上,变式题4 与例5 如出一辙.

变式题5(2019年厦门市九年级期末质检试题,24)已知P 是⊙O 上一点, 过点P 作不过圆心的弦PQ, 在劣弧PQ 和优弧PQ 上分别有动点A,B (不与P,Q 重合),连接AP,BP.若∠APQ=∠BPQ.

(2) 如图12,连接AB,交PQ 于点M,点N 在线段PM上(不与P,M 重合),连接ON,OP,若∠NOP+2∠OPN =90°,探究直线AB 与ON 的位置关系,并证明.

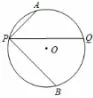
图11

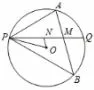
图12

评注变式题5(2)整体上考查的内容与例5 和变式题4基本一致,但细分起来,又有所不同,主要在于空间观念——识别或构造等圆周角结构、半径等腰、“垂径定理结构”;推理能力——能结合题目条件中的角的数量关系联想图形性质,并能选择恰当、简捷的基本图形建立已知量与未知量之间的简捷联系,利用图形性质实现转化.

笔者曾以17 和18年厦门质检题作为学生测试的题目,19年参与阅卷,恰好批改的也是24 题,这三道题的第二问得分率比较低.在讲评试卷时,如果结合已知条件进行局部推导,较多的学生是可以做到的,但较少有学生能够做到完整推导,足以反映上述试题不再是单纯的技能叠加,说明本题重在考查学生的数学能力,区分学生的层次.而学生在该题得分较低的原因正是缺乏技能叠加之间的嵌合.如何嵌合才能使学生在这一块尽量能得高分? 可以从以下方面进行实施：一是构造辅助线的能力.学生能够从平时的练习中总结圆中常用的辅助线.比如例5图11 中连接OA;变式题4 中能够看出垂径定理的影子从而补全半圆并延长MC,能够由中点联想到中位线进而作出辅助线;变式题5 图11 中连接OQ、OB.二是这三道题目重点考查了划归与转化的数学思想,而对数学思想的理解,是串联局部知识网络的关键环节,从而对数学知识进行宏观把控.这就需要学生平时练习时注意比较同类型题目之间的区别与联系,归纳特征,总结方法.

四、感悟

在复习教学中, 对圆周角定理的梳理是“由点成面”的过程,即在基础知识上理清吃透知识点;在基本技能上用题目“包抄”知识点,强化局部知识网络的联系,形成解决知识点的内驱力;在基本能力和基本思想上,需要清醒地认识到：“数学中最重要的是动脑、而不是动手,基本能力和基本思想往往以已有的东西(活动、运演、概念、理论等)作为直接的分析对象,并就主要表现为由较低的抽象层次上升到了更高的层面”[4].通过“四基”复习路径,不仅复习了圆周角定理,还串联了其它知识点,可以使不同层次的学生得到提高,能够有效因材施教,提升中考数学复习的质量.此外,“四基”复习路径有助于学生更好地实现数学能力和数学思想的形成,有效衔接初高中数学知识的学习.