利用判别式法求二次分式函数的值域

陕西省城固师范学校(723200) 刘敬民

而对于b2-4ac ≥0 时的函数值域问题采取回避的态度.实际上此法可扩展适用于所有的二次分式函数,在解题过程中要注意判断是否为函数值及定义域对函数值的影响,检验Δ=0 时的情形.

判别式法又名方程法是用方程的观点求解的,也就是把函数y = f(x)同解变形为x 的一元二次方程,利用Δ ≥0求得原函数的值域.此法不仅适用于分式函数而且适用于二次分式函数,还适用于解析式中含有根号的情形.用此法求二次分式函数值域解题步骤和方法容易被学生掌握,但知其法不明算理的情况应引起我们的重视和关注.

命题一如果二次分式函数中至少有一个不为零)的分子分母互素,那么关于x 的分式方程

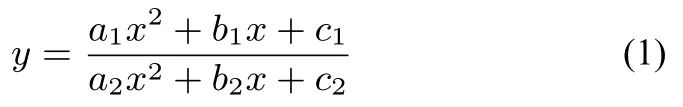
与关于x 的整式方程

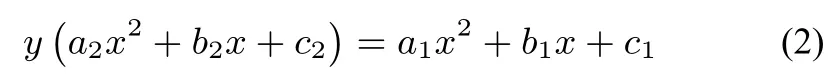
同解.

证明设 x0是 (1) 方程的一个根, 即 y =由于有成立, 这说明x0也是方程(2)的一个根.

反过来, 设x0是方程(2) 的一个根, 即此时有b2x0+ c20, 否则有这样a1x2+b1x+c1与a2x2+b2x+c2有公因式(x-x0),与已知分子分母互素矛盾.于是有成立.这说明x0也是方程的根.

因此,方程(1)与方程(2)是同解的.

2.分子分母互素的二次分式函数值域

命题二如果二次分式函数a20)的分子分母互素,那么

证明由命题一知方程与方程y(a2x2+b2x+c2)= a1x2+b1x+c1是同解的,进一步有同解方程

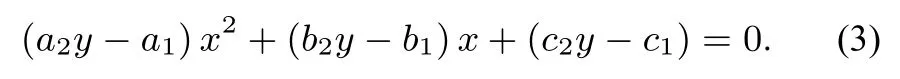
设a2y - a10, 因为x 是实数, 故判别式非负.即Δ = (b2y-b1)2-4(a2y-a1)(c2y-c1) ≥0,此时由同解变形方程(3)得到的每一个x 的值均有a2x2+b2x+c20,也就是说由解出的任意一个y 均为函数值.

设a2y-a1=0,此时a20 否则a1=0,a1,a2同时为零与已知矛盾.因而有当即a1b2a2b1时, 由方程(3)得由于方程(1)(2)(3)同解, 有为相应的函数值; 当时,由于函数的分子分母互素,因此关于x 的方程(3)无解,不是函数值.

又a2y-a1= 0 时,Δ = (b2y-b1)2≥0 显然成立,因此当且a20 时,所求值域要从Δ ≥0 的解集中去掉

3.分子分母有公因式的二次分式函数值域

命题三如果二次分式函数a20) 的分子分母有唯一公因式(x - m), 那么函数的值域为Δ ≥ 0 的解集中去掉和后的部分, 即y =且和或y =

证明设x1和x2分别为方程a1x2+b1x+c1= 0 和a2x2+b2x+c2=0 的另外一个根且x1x2,于是函数y =即：可化为方程

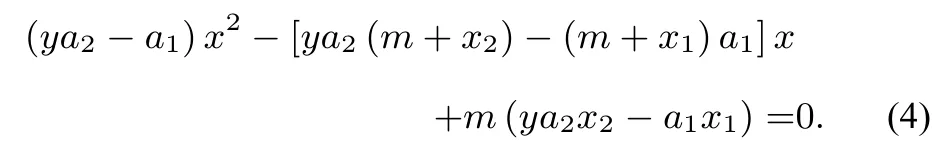
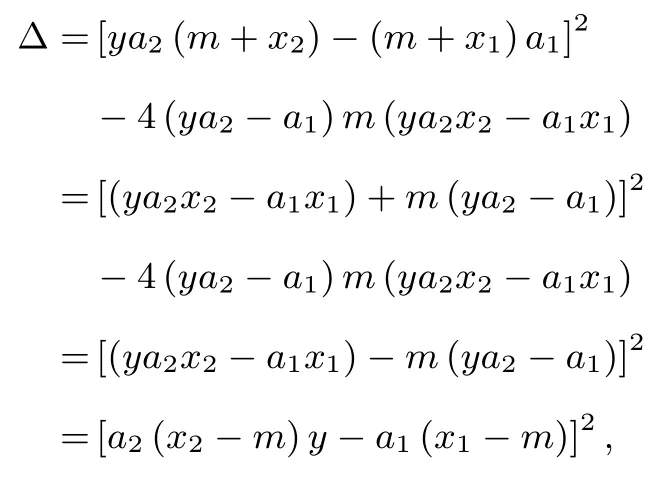
设ya2-a10,有于是当 Δ ＞ 0 时, 由方程 (4) 得 x =进 一 步 有：x=或者x=m 增根;

当Δ = 0 时, 即ya2x2- a1x2= (ya1-a1)m 等价于：a2(x2-m)y - a1(x1-m) = 0(x2m 时), y =此时是增根.也就是说Δ = 0, x2m 时方程(4) 有解而原函数的值不存在, 因此要从Δ ≥0 的解集中去掉

又, 当 x2= m 时, 由于 x1x2, Δ =[a2(x2-m)y-a1(x1-m)]2=而Δ ＞0 时, 不等式解集中y 均存在相应的x(xx1和xm)使得y 为函数值.因此,x2=m 对于Δ ≥0 的解集没有影响.

设ya2- a1= 0, 即由方程(4) 可得：a1(x2-x1)m = ma1(x2-x1), 由于a10,x1x2, 则x = m 为增根, 因此不是函数值.又ya2- a1= 0 时, Δ = [ya2(x2-m)-a1(x1-m)]2=[a1(x2-m)-a1(x1-m)]2=因此,要从Δ ≥0 的解集中去掉

4.小结与应用举例

以上分情形讨论了用判别式法就求解二次分式函数值域时分子分母可能出现的各种情形,一言蔽之,倘若事先不去考虑各种可能的因素, 需要判断是否为函数值以及Δ=0 时的检验.

例1求函数且x-3,x1)值域.

解由已知得yx2+ 2xy - 3y = x2- 2x + 3, 即(y - 1)x2+ 2(y + 1)x - 3(y + 1) = 0.当y = 1 时, 得为函数值.当y1 时,Δ=4(y+1)2+12(y+或y ≤-1.检验：时,x=3;y =-1 时,x=0.和y =-1 均为函数值.

例2求函数且x-3,x1)的值域.

解由已知得yx2+ 2xy - 3y = 2x2+ 4x + 1, 即(y-2)x2+2(y-2)x-3(y+1)=0.

(1) 当y =2 时,得-7=0,x 不存在.因此,y =2 不是函数值.

例3求函数(x ∈R 且x3)值域.

解由题有xy-3y =x2-3x+2,即x2-(y+3)x+3y+2=0,有Δ=(y+3)2-4(3y+2)=y2-6y+1 ≥0,或检验：时,时,均为函数值.值域为

类似地,可以继续用判别式法求下列分式函数值域.