重庆市万州区2019年初三抽考试题26题第(3)问多维赏析

重庆市万州高级中学(404100) 何亮

本次抽考的结果下来,我们班上130 分以上的29 人,140分以上的13 人,146 分左右的10 人,可见整个卷子的难度不大,但没有满分.研究下来发现,问题主要出现在26 题第(3)问,全班只有一人做对,下来后我和学生们一起将这个题梳理了一遍,将他们的一些想法落实下来,得到了许多方法,现将它呈现下来.

试题呈现如图1：抛物线y = -x2+2x+3 的图像与x 轴交于点A、B,与y 轴交于点C,连接BC.

(1) 求直线BC 的解析式;

(2) 如图2, 点P 是抛物线在第一象限内的一点, 作PQ//y 轴交BC 于点Q,当线段PQ 的长度最大时,在x 轴上找到一点M,使PM +CM 的值最小,求PM +MC 的最小值;

(3) 抛物线的顶点为点E,在抛物线上是否存在一点N,使得直线AN 与直线AE 的夹角为45 度.若存在请直接写出满足条件的点N 的坐标,若不存在,请说明理由.

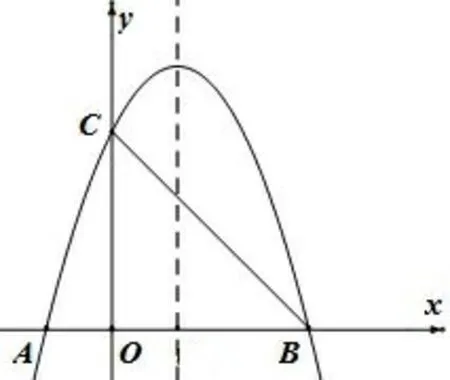
图1

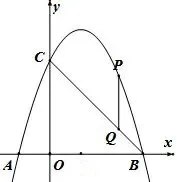
图2

第(3)问题分析：问题的本质是求将直线AE 绕着点A 旋转45°后所得的直线与抛物线的交点.如图3 可以发现,由于旋转的方向可以分为顺时针和逆时针,作出的直线有两条,且这两条直线互相垂直,所以有两个符合条件的点N.求出第一个N1就可以顺带求出第二个N2的坐标,现在我们先来求N1.

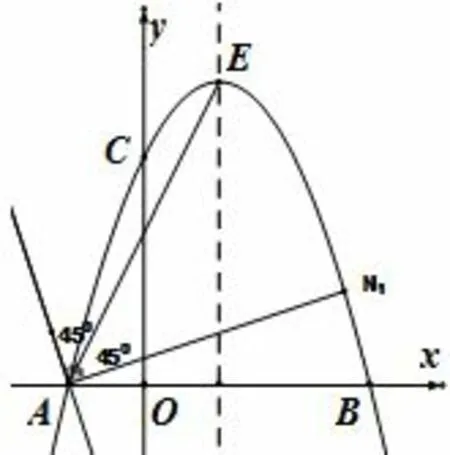
图3

问题解决学生思路1：先求直线与x 轴、y 轴的交点,确定直线表达式再求点N1.

方法1如图4, 过点F 作AD 的垂线交AD 于点G,连接FG.因为A(-1,0), E(1,4), 所以lAE: y = 2x+2,所以D(0,2).在R T △AOD 中, AO = 1, OD = 2,所以故在△ADF 中有3个条件我们可以解这个三角形.设GF = x, 因为设AG = x, 则GD = 2x,又因为所以所以所以由得直线AF 表达式：联立得

方法2如图5, 设直线AE 交y 轴于点D, 直线AN1交y 轴于点F, 过点D 作DG⊥AN1交AN1于点G.由法1 知OD = 2, AO= 1, AD =且∠DAG = 45°,所以设OF = x, 则DF = 2 - x,显然△AOF ≈△DGF,所以即所以或x=-3(舍去),所以同理方法1 可得

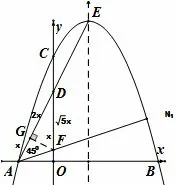
图4

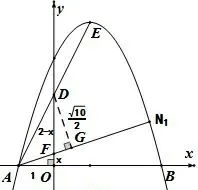
图5

学生思路2：不一定非要求直线与y 轴的交点,只要是直线上面的任意一点都可以.由45°可能会想到去构造等腰直角三角形.而用好这个等腰直角三角形的方法我给的是三垂直图形.

方法3如图6, 过点E 作AE 的垂线交AN1于点M, 再过E 作x 轴的平行线, 过A、M 作垂线交于点H、K.因为∠H = 90°,∠AEM = 90°, 所以∠HAE + ∠HEA = 90°,∠KEM + ∠HEA = 90°, 所以∠HAE = ∠KEM, 且∠H = ∠K = 90°,AE = AM, 所以ΔAEH ～= EMK(AAS),所以EK = AH,KM = HE,又因为A(-1,0)、E(1,4), 所以AH = 4, HE = 2, 所以EK = 4,KM = 2,所以M(5,2),所以直线AM 的表达式为同理方法1 可得

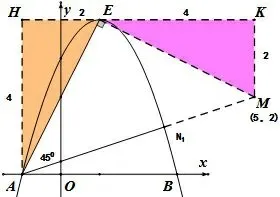
图6

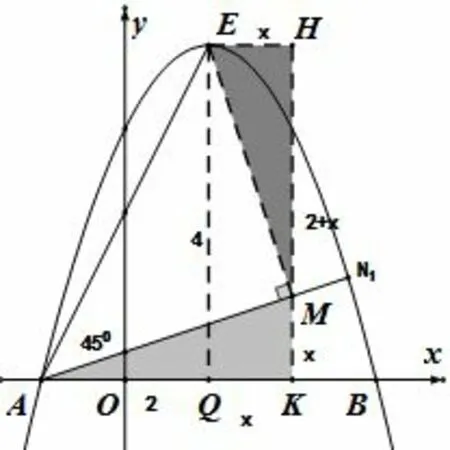
图7

方法4如图7, 过点E 作AN1的垂线交于点M, 过M 作y 轴的平行线,再过A、E 作平行线的垂线于点H、K,过E 作x 轴垂线交于点Q.同理方法3, 我们依然可以得△EHM ～= △MKA,所以EH = MK,HM = AK.因为A(-1,0)、E(1,4), 所以AQ = 2,EQ = 4.设QK = x, 则EH =x,MK =x,HM =2+x,所以x+(2+x)=4,所以x = 1,所以M(2,1),故直线AM 的表达式为同理可以求

学生思路3：是否可以直接求N 的坐标而跳过直线表达式呢?

方法5如图8, 过点N1向直线AE 作垂线交AE于点M, 过点M 作x 轴的平行线, 过A、N1作平行线的垂线交平行线于点H、K.因为A(-1,0)、E(1,4),所以直线AE : y = 2x + 2.设M(m,2m + 2), 所以AH =2m+2,HM =m+1,又因为△MHA ～= △N1KM,所以MK = AH = 2m + 2, KN1= MH = m + 1, 所以N1坐标为(3m+2,m+1), 将它代入抛物线的表达式y =-x2+2x+3,得-(3m+2)2+2(3m+2)+3=m+1,所以m=-1 或所以N1(-1,0)(舍)或

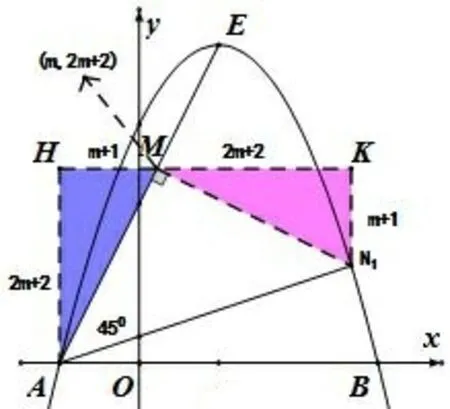
图8

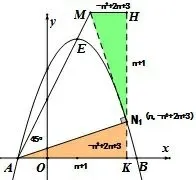
图9

方法6如图9,过N1作直线AN1的垂线交AE 于点M,过N1作y 轴的平行线,过A、M 作平行线的垂线交于点H、K.设N1的坐标(n,-n2+2n+3),所以AK = n+1,KN1=-n2+2n+3,又因为△MHN1～= △N1KA,所以MH =KN1=-n2+2n+3,HN1=AK =n+1,所以M的坐标为(n2-n-3,-n2+3n+4),将其代入y =2x+2中得2(n2-n-3)+2 = -n2+3n+4,所以n = -1 或所以N1(-1,0)(舍)或

最后我们可以仿照前面的方法继续求得N2(6,-21),所以点N 的坐标为或(6,-21).

总结和同学们一起探讨完这个题目后,同学们有种恍然大悟的感觉.原来自己的一些想法都是对的,但是如何进一步深入挖掘和分析直至得到我们想要的结果还需要向老师一样细致的分析和抓好基础.这个题目看似简单,但在这些方法中考查到了除二次函数和一次函数以外的其他知识,包括解三角形、相似、全等,是一个具有思维深度的好题.